1 Język : akto komunikacji , pojecie znaku , pojecie języka i jego funkcje , język sztuczny i naturalny , j język sformalizowany i niesformalizowany , język przedmiotowy i metajęzyk

AKT KOMUNIKACJI

Produkuje Interpretuje

Nadawca Znak Odbiorca

wyraża

przekazuje pojmuje

komunikat,

informacja

znak - dowolny przedmiot lub zjawisko fizyczne służące zakomunikowaniu komuś czegoś wobec obowiązywania pewnych konwencji dotyczących zasobu jego rozumienia

Język - jest to system umownych znaków słownych

• Funkcję języka:

• funkcja informacyjna - przekazuje informacje

• funkcja estetyczna - zwrócenie uwagi na sposób organizacji komunikatu, zasada przezroczystości znaku, w trakcie komunikacji znakowej nie zauważana jest na ogół forma znakowa

• funkcja ekspresywna - wyrażanie i wzbudzenie pewnych stanów wewnętrznych, np. uczuć

• funkcja persfazyjnosugestywna - na plan pierwszy wysuwa się zakazywanie czegoś lub jakiegoś działania, funkcja ta też przekonuje kogoś do czegoś

• funkcja fatyczna - występują wypowiedzi podtrzymania, rozpoczęcia lub zakończenia rozmowy

1. Język naturalny a sztuczny, język sformalizowany a niesformalizowany, język zinterpretowany a nieinterpretowany, język przedmiotowy a metajęzyk.

JĘZYK NATURALNY język potoczny i używany przez nas na co dzień, przekaz kulturowy. Słownik tego języka jest zbiorem otwartym	JĘZYK SZTUCZNY język zbudowany specjalnie dla określonych celów. Słownik tego języka jest zbiorem zamknięty
JĘZYK SFORMALIZOWANY Język w szczególny sposób opisany, język spełnia określone postulaty efektywności	JĘZYK NIESFORMALIZOWANY Słownik j nie jest ustanowiony . Reguły nie są formułowane
JĘZYK ZINTERPRETOWANY język posiadający reguły znaczeniowe, wyrażenia zostały podporządkowane reguły	JĘZYK NIEZINTERPRETOWANY nie wymaga podania reguł znaczeniowych, charakteryzacja poprzez reguły składniowe i słownikowe
JĘZYK PRZEDMIOTOWY Język będący przedmiotem rozważań	METAJĘZYK język służący do opisywania pewnego innego języka (tzw. języka przedmiotowego), zawierający nazwy wyrażeń tego języka, nazwy właściwości tych wyrażeń oraz związków, jakie między nimi zachodzą.

2 gramatyka kategorialna : pojecie kategorii gramatycznej , rodzaje kategorii gramatycznych

Kategoria Gramatyczna - a języka `' j `' nazywamy zbiór wszystkich tych wyrażeń tego języka , którymi możemy bez utraty poprawności gramatycznej , możemy zastąpić wyrażenie a w dowolne wyrażenie

Β języka ,, J `'

Dwa wyrażenia należą do tej samej kategorii gramatycznej wtw. Gdy są zastępowalne w danym wyrażeniu złożonym bez utraty poprawności gramatycznej

Kategorie gramatyczną dzielimy na :

- samodzielne ( podstawowe ) -

- Nie samodzielne ( pochodne)- różnego rodzaju funktory - nie stanowia samodzielnych jednostek

2. 3 Nazwa, jej desygnat i treść językowa (konotacja). Klasyfikacja nazw.

• Nazwa - jest to dowolne wyrażenie, które może wystąpić w roli podmiotu lub orzecznika w zdaniu

podmiotowo - orzecznikowym, czyli w zdaniu o budowie <podmiot> jest <orzecznik> np. Fido jest psem

• Desygnat - jest to przedmiot oznaczony przez tą nazwę. Zbiór wszystkich desygnatów danej nazwy tworzy jej zakres. Posiada wiele cech ważnych lub mniej ważnych.

• Treść językowa)konotacja) - jest to zbiór cech, które użytkownik języka używając tej nazwy przypisuje wszystkim jej możliwym desygnatem. Pewne cechy przysługują desygnatom w sposób istotny (konstytuowany) lub pochodny (konsekutywny).

Np. Kwadrat

• konstytutywne - czworoboczność, prostokątność, równoboczność

• konsekutywne - posiadanie równych przekątnych

• Podział nazw:

• ze względu na budowę:

• proste (jeden wyraz)

• złożone (kilka wyrazów)

• ze względu na liczbę desygnatów:

• puste (brak desygnatów)

• jednostkowe (dokładnie jeden desygnat)

• ogólne (więcej niż jeden desygnat)

• ze względu na sposób wskazywania desygnatów:

• generalne (nazwa przysługująca przedmiotowi ze względu na cechy jakie są mu przypisywane), np. kwadrat

• indywidualne (nazwa przysługująca przedmiotowi ze względu na ustawienia), np. akt chrztu

• ze względu na rodzaj desygnatu:

• konkretne (desygnat osobowy, rzeczy), np. krasnoludek

• abstrakcyjne (nazwy podmiotów abstrakcyjnych - cechy stosunków zdań), np. białość, przyjaźń, cisza

• ze względu na strukturę wewnętrzną:

• zbiorowe (desygnat jest pewną całością złożoną z części [argumentów], np. las, biblioteka

• nie zbiorowe (desygnaty - są przedmiotami prostymi), np. stół

4 zdanie proste i złożone , zdanie analityczne i kontradyktyczne , zdanie syntetyczne

Zdanie - jest to jednostka komunikacyjna. Oznacza wartości logiczne i oznacza stany lub sytuacje

Zdanie Proste - Zdanie , w którym nie występuje żaden spójnik

Zdanie złożone - Zdanie , w którym nie występuje żaden spójnik

Zdanie analityczne - zdanie, które jest prawdziwe na mocy swej struktury i znaczenia występujących w nim wyrażeń np. Kwadrat ma cztery boki. Poznań leży nad Wartą lub nie leży nad Wartą

• Zdanie kontradyktyczne - (wewnętrzne spostrzeżenie) zdanie, które jest fałszywe na mocy swej struktury i znaczenia występujących wyrażeń np. Trójkąt ma cztery boki. Poznań leży i nie leży nad Wartą.

Zdanie syntetyczne - zdanie , którego stwierdzenie prawdziwości lub fałszywości wymaga kontaktu poznawczego z rzeczywistością

5 spójnik ekstensjonalny a intensjonalny .

3. Spójnik ekstensjonalny a spójnik intensjonalny.

• Spójnik ekstensjonalny, czyli prawdziwościowe, np. Nieprawda, że A

^{prawda 0 fałsz}

Charakteryzuje się tym ,że wartość logiczna zdania złożonego, utworzonego przy jego pomocy, zależy tylko od wartości logicznych zdań składniowych np. „Jest prawdziwe, że”

„i”

„lub”

„ani…ani”

• Spójnik intensjonalny - to taki, że wartość logiczna zdania złożonego utworzonego przy jego pomocy zależy także od treści zdań.

np. możliwe, że A możliwe, że B

^{0 0}

Wiadomo, że

Myślę, że.

• 
  implikacja -> połączenie formuły (A)->(B) formuła przed znakiem implikacji to poprzednik, a za znakiem implikacji to następnik. Spójnik czytamy: jeżeli.., to; Jeżeli <poprzednik>, to < następnik>; jeśli.., to; o ile… to. Zdania nazywamy warunkami lub okresy warunkowe. Implikacja formuły (A) (B) jest fałszywa, gdy poprzednik jest prawdziwy, a następnik fałszywy.

• 
  równoważność ≡ - (A) ≡ (B) czytamy: wtedy i tylko wtedy. Równoważność formuły jest prawdziwa, gdy dwa składniki są prawdziwe. Każde zdanie równoważne prawdziwe jest prawdziwe i odwrotnie

• 
  negacja „~” - polega na poprzedzeniu formuły A, np. ~(A) czytamy: nieprawda, że; nie jest tak; nie. Zdania nazywamy negacjami lub zaprzeczeniem. Gdy formuła A jest prawdziwa to negacja jest fałszywa i gdy formuła jest fałszywa to negacja jest prawdziwa.

• 
  koniunkcja ^ - polega na połączeniu dwóch formuł, np. (A)^(B) formuły te nazywamy czynnikami. Symbol ten oznacza: i, oraz, a, ale, lecz, natomiast. Komunikacja jest prawdziwa gdy oba czynniki są prawdziwe, natomiast fałszywa, gdy co najmniej jeden czynnik jest fałszywy.

• 
  alternatywa v - połączenie formuły (A)v(B); formuły te nazywamy składnikami. Zdanie nazywamy alternatywą; spójnik to: lub, bądź. Alternatywa jest fałszywa, gdy oba składniki są fałszywe, natomiast jest prawdziwa, gdy co najmniej jeden składnik jest prawdziwy. Używa się go w sensie wykluczającym, gdy składniki maja różne znaczenia logiczne, np. Poślubię albo Adama albo Marka. Jeżeli alternatywa jest prawdziwa, któryś z jej składników jest fałszywy, to drugi składnik musi być prawdziwy.

6 Język KRZ ( słownik , formuły ) Budowanie schematów zdań .

• Definicja formalna języka KRZ:

• każda zmienna zdaniowa jest formułą KRZ

• jeżeli A,B są formułami KRZ to wyrażenia:

~(A);(A)^(B);(A)v(B);(A)->(B);(A)≡(B); są formułami KRZ

• nie ma innych formuł poza zmiennymi zdaniowymi i takimi formułami, które można zbudować dzięki zastosowaniu reguły 2

Przykłady

Formułami są: p; ~p; ~~p; p ^ q; ~(p -> ~q)

Formułami nie są: p ~q; p -> q; ~p -> q; ~pq

• Definicja podformuły - dozwoloną cześć formuły A, która sama jest formułą nazywamy podformułą formuły A. Do podformuły formuły A zaliczamy samo A.

Przykłady

Formułą jest: p -> ~(q ^ ~r)

jej podformułami są:

p; q; r; ~r; q ^ ~r; ~(q ^ ~r)p -> ~(q ^ ~r)

p -> ~(q ^ ~r)

p ~(q ^ ~r)

q ^ ~r

q ~r

^ r

• Schematy zdań

• Jeśli mówisz nie prawdę ale czynisz to nie świadomie to nie kłamiesz

Niech p - mówisz nieprawdę

q - czynisz to nieświadomie

r - kłamiesz

wówczas: (p^ q) ~ r

• Zdam egzamin z logiki lub go nie zdam

Niech p - zdam egzamin z logiki

wówczas: p v ~p

• Nie potrafisz kontrolować swoich rozumowań, wtw gdy nie znasz zasad logiki

Niech p - potrafisz kontrolować swoich rozumowań

q - znasz zasady logiki

wówczas: ~p ≡ ~q

• Jeżeli wprowadziłeś alternatywę, to o ile jeden jej składnik nie jest fałszywy to wypowiedziałeś zdanie prawdziwe.

Niech p - wprowadziłeś alternatywę

q - jeden jej składnik jest fałszywy

r - wypowiedziałeś zdanie prawdziwe

wówczas: p (~q r)

• Jeżeli wygrasz ten proces, to otrzymasz znaczny spadek, a jeśli go przegrasz to będziesz musiał opłacić znaczne koszty sądowe.

Niech p - wygrasz ten proces

q - otrzymasz znaczny spadek

r - go przegrasz

s - będziesz musiał opłacić znaczne koszty sądowe

wówczas: (p q) ^ (r s)

7 Pojęcie Tautologii i kontrtautologii KRZ . Wybrane tautologie KRZ

• Wartościowanie - wartościowaniem formuł w KRZ nazywamy dowolną funkcję V ze zbioru formuł KRZ w zbiór wartości logicznych (0,1) taką, że dla dowolnych formuł A i B zachodzi:

Jeżeli v(A) v(B) to v(~A) v(A v B) v(A ^ B) v(A -> B) v(A ≡ B)

v(A)	v(B)	to	v(~A)	v(A v B)	v(A ^ B)	v(A B)	v(A ≡ B)
1	1		0	1	1	1	1
1	0		0	0	1	0	0
0	1		1	0	1	1	0
0	0		1	0	0	1	1

v(A) wartość logiczna formuły A

• Wnioski!

• wartość formuły jest jednoznacznie zdeterminowana wartościami jej podformuły

• znając wartość podformuły można wyliczyć wartość całej formuły

• z punktu widzenia wartościowania formuł wyróżniamy 3 rodzaje:

• formuły, które dla każdego wartościowania przyjmują wartość 1- tautologie (schematy zdań wyłącznie prawdziwych)

• formuły,które dla każdego wartościowania przyjmuje wartość 0 - kontr tautologie (schematy zdań wyłącznie fałszywych)

• formuły, które dla pewnych wartościowań przyjmują wartość 0 lub 1 (dla innych)

• Tautologia i kontrtautologia

• formuła A jest tautologia klasycznego rachunku zdań i tylko wtedy, gdy dla każdego wartościowania v v(A)=1

• formuła A jest kontr tautologią klasycznego rachunku zdań kiedy, tylko wtedy, gdy dla każdego wartościowania v v(A)=B

• Wynikanie semantyczne - z formuł A1….An wynika semantycznie na gruncie KRZ formuła B wtw, gdy implikacja (A1 ^…..^ An) -> B

Jest tautologią KRZ

• Przykład 1

• jeśli wnioskujesz dedukcyjnie to wniosek wynika logicznie z przesłanek.

• wniosek nie wynika logicznie z przesłanek, wynika semantycznie (logicznie) zdanie.

• nie wnioskujesz dedukcyjnie

[(p -> q) ^ ~q] -> ~p

Jest tak bo implikacja a ^ b -> c podpada pod prawo modus tollendo tollens

[(p -> q)^~q] -> ~p

Wnioskowanie - jakakolwiek skończona co najmniej dwuelementowa sekwencja zdań, z których ostatnie jest wnioskiem a wszystkie zdania poprzedzające wniosek to przesłanki.

Wnioskowanie logiczne (poprawne lub dedukcyjne) - jest wtedy, gdy schematem jest pewna niezawodna reguła, która prowadzi od prawdziwych przesłanek do prawdziwych wniosków.

schematy przesłanek

Schemat wniosku

są to formuły języka KRZ

Substancja S jest kwasem lub zasadą. Jeżeli S jest kwasem to barwi papierki lakmusowe na czerwono. Ale S nie barwi papierka na czerwono - przesłanki

Zatem S jest zasadą,

Schemat 1

p=1
} p v q

r=1 } 1 p -> r

r=0 }

sprzeczność 0

Pozostaje sprawdzić czy reguła jest niezawodna.

• Reguła wnioskowania - (schematem wnioskowania, wyrażaną w języku KRZ) nazywamy dowolny skończony, co najmniej dwu wyrazowy ciąg formuł języka KRZ. Ostatnią formułę nazywamy schematem wniosku, a formułę wcześniejszą schematem przesłanek.

• Przykłady:

p, q / p ^ q

p≡ ~q, p ≡ q / (p ≡ ~q) ^ (~p ≡ q)

p -> ~~q, q / ~p

reguła niezawodna - reguła A1….An / B jest niezawodna wtw, gdy implikacja (A1^…^An ) -> B jest tautologia KRZ wtw, gdy z formuł A1….An wynika semantycznie formuła An w pierwszym przypadku reguła jest zawodna.

• Twierdzenie

Jeżęli reguła A1…An / B jest niezwodna, a formuła A1…An uzyskuje wartość 1 to formuła B też uzyskuje wartość 1.

Zakładamy, że:
jest niezawodna

i że

r(A1) = 1,…,r(An) =1

r(B) = 0

r((A1 ^…..^ An) -> B) = 0

(A1 ^….^ An) -> nie jest tautologią.

• Przykłady reguł niezawodnych

Reguła oparta na prawie modus Ponendo ponens

Prawo modus tollendo

Sylogizm hipotetyczny

(p -> q) -> (~q -> ~p)

Prawo redukcji do absurdu

Każda tautologia jest zadaniem prawdziwym, ale nie każde zadnia prawdziwe jest

A -> B

1 -> ?

• Tautologie dotyczące zdań sprzecznych

• PRAWO WYŁĄCZNEGO ŚRODKA

p v ~p

• PRAWO NIESPRZECZNOŚCI

~(p ^ ~q)

• NIERÓWNOWAŻNOŚCI SPRZECZNOŚCI

~(p ≡ ~p)

• DUNSA SZKOTA

(p ^ p) -> q

• Tautologie dotyczące zaprzeczenia

• SILNE PRAWO PODWÓJNEJ NEGACJI

~p ≡ p

• PRAWO NEGOWANIA KONIUNKCJI

~(p ^ q) ≡ (~p v q)

• PRAWO NEGOWANIA ALTERNATYWY

~(p ^ q) ≡ (~p ^ ~q)

• PRAWO NEGOWANIA RÓWNOWAŻNOŚCI

~(p ≡ q) ≡ [(p ^ ~q) v (q ^ ~p)]

• PRAWO NEGOWANIA IMPLIKACJI

~(p -> q) ≡(p ^ ~q)

• Tautologie dotyczące implikacji

• PRAWO SYLOGIZMU HIPOTETYCZNEGO

(p -> q) -> [(q -> r) -> (p -> r)]

• MODUS PONENDO PONENS (sposób na potwierdzenie przez potwierdzenie)

[(p -> q) ^ p] ->q

• MODUS TOLLENDO TOLLENS (sposób na odrzucenie przez odrzucenie)

[(p -> q) ^ ~q] -> ~p

• PRAWO REDUKCJIDO ABSURDU

[(p -> q) ^ (p -> ~q)] -> ~p

• Tautologie dotyczące równoważności

• PRAWOROZKŁADANIA RÓWNOWAŻNOŚCI

• (p ≡ q) ≡ [(p -> q) ^ (q -> p)]

• PRAWO OBUSTRONNEGO NEGOCJOWANIA RÓWNOWAŻNOŚCI

(p ≡ q) ≡ (~p ≡ ~q)

9 stosunki między zdaniami wynikanie semantyczne , logiczna równoważność,

sprzeczność . wykluczanie , dopełnianie .

• Wynikanie semantyczne - z formuł A1….An wynika semantycznie na gruncie KRZ formuła B wtw, gdy implikacja (A1 ^…..^ An) -> B

Jest tautologią KRZ

• Przykład 1

• jeśli wnioskujesz dedukcyjnie to wniosek wynika logicznie z przesłanek.

• wniosek nie wynika logicznie z przesłanek, wynika semantycznie (logicznie) zdanie.

• nie wnioskujesz dedukcyjnie

Jest tak bo implikacja a ^ b -> c podpada pod prawo modus tollendo tollens

[(p -> q)^~q] -> ~p

Logiczna równoważność - Zdanie z i w są logicznie równoważne wtw gdy równoważność jest tautologia klasycznego rachunku zdania

s(z) wtw s(w)

( p—q) wtw. ( p v -q )

Zdania

10 Pojęcie reguły wnioskowania i niezawodnej reguły wnioskowania

Reguła wnioskowania - regułą { schematem) wnioskowania wyrażoną w języku KRP nazywamy dowolny skończony co najmniej dwuwyrazowy ciąg formuł języka KRZ . Ostatnią formułę nazywamy schematem wniosku , a f formuły wcześniejsze elementem przesłanek

Przykłady :

P , q / p^ q

P wtw. -q , -p wtw.q / ( p wtw. -q ) ^ ( -p wtw. q )

P -- -q , q / -p

Reguła niezawodna wnioskowania - Reguła A1 …. An / B jest niezawodna wtw. implikacja ( A1, 1……1An ) - B jest tautologia KRZ , wtw x formuł

A1, ….., An wynika semantycznie na gruncie KRZ formuła B .

W przeciwnym przypadku reguła jest zawodna

11 Dedukcja , wnioskowanie entymematyczne , błędy wnioskowania .

Wnioskowanie entynematyczne - nazywamy wnioskowanie , w którym występuje przesłanka entynematyczna ( ukryta } tj. przesłanka nie wymieniona we wnioskowaniu z powodu uznania jej za oczywista .

Wnioskowanie Entynematyczne jest ( formalnie ) poprawne jeśli wniosek wynika logicznie z przesłanek

Błędy wnioskowania :

A ) Błąd naturalny - błąd wniosk. Gdy do uzasadnienia wniosku używa się fałszywych przesłanek ( wystarczy , że jest błąd )

B)Błędne koło ( bezpośrednie) - błąd wnioskującego polegający na wykorzystaniu do uzasadnienia wniosku W wykorzystuje się wniosek W bądź zadanie , które jest z tym wnioskiem trywialnie równoważne . np. dusza jest nieśmiertelna gdyż nigdy nie umiera .

Np. Ludzie są niegodziwi bo natura ludzka jest zepsuta , a to , ze natura jest zepsuta związane jest z tym , ze ludzie są niegodziwi .

C) Błąd formalny - powstaje gdy wnioskujący jest przekonany , że wnioskuje dedukcyjnie , tymczasem reguła przez , która wnioskuje jest zawiodna tzn. wniosek nie wynika logicznie z przesłanek , nawet po uwzględnieniu przesłanek ukrytych .

Np. Błąd wnioskowania z prawdziwości następnika implikacji .

P - Q , Q

P

Jeżeli lekarstwo było skuteczne to chory wyzdrowiał a ponieważ chory wyzdrowiał lekarstwo było skuteczne . ( przyczyny mogły być inne )

D) Błąd wnioskującego z negacji poprzednika implikacji

P-Q, -P

-Q

np. jeżeli rozumujesz poprawnie to dochodzisz do prawdziwej konkluzji , ponieważ nie rozumujesz poprawnie nie dochodzisz do prawdziwej konkluzji .

E ) Błędna konwersja

P - Q

-p -- -q

np. Jeżeli oskarżony jest winny to był na miejscu zbrodni skąd jeśli jest niewinny to nie był na miejscu zbrodni { formalnie niepoprawnie}

12 ) Pojęcie języka pierwszego rzedu , język KRP : Słownik , formuła atomowa , formuła , zasięg kwantyfikatora , zmienna wolna i zmienna związana , zdanie : budowanie schematów zdań

Język pierwszego rzędu - To system logiczny , w którym

Kwantyfikatory mogą mówić tylko o obiektach , nie zaś o ich zbiorach

• Klasyczny rachunek predykatów

• 
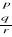
  P₁ Każdy jest śmiertelny

• P₂ Sokrates jest człowiekiem

• W Sokrates jest śmiertelny

Zdanie proste to zdanie przypisujące pewną własność

Przykład

Ewa kusi Adama. R(a,b)

a R b

Predykat - wyrażenie, które wyraz z jedną bądź wieloma wyrazami tworzy zdanie.

Ewa kusi naiwnego Adama R(a, φ(b))

nazwa złożona = funktor

φ(b)

naiwny - φ

w klasycznym rachunku predykatów występują zmienne nazwowe (indywidułowe) = x, y, z, r, x1…

• Można wyróżnić schematy zdaniowe, np.

x kocha y, uwodzi zaś z, żyje natomiast z r.

lub

x + y = z

• Wszyscy są leniwi (predykat)

L(x): x jest leniwy

kwantyfikator generalny (ogólny, duży)

lub

czytamy: dla każdego

dla dowolnego

dla wszystkich

Rola: wiązanie zmiennych

Zdanie ogólno twierdzące

: dla każdego x, x jest leniwy.

• Niektórzy są leniwi.

lub kwantyfikator egzystencjalny (szczegółowy, mały)

czytamy: istnieje takie…, że…

dla, pewnego

niektóre

dla przynajmniej jednego

Rola: wiązanie zmiennych

Zdanie szczegółowo twierdzące

: istnieje takie x, że x jest leniwy.

• Nikt nie jest leniwy

zdanie ogólno przeczące

• niektórzy nie są leniwi.

zdanie szczegółowo przeczące

• Każda kobieta jest gadatliwa

K(x): x jest kobietą

G(x): x jest gadatliwa

K(x) -> G(x): jeżeli x jest kobietą, to x jest gadatliwa.

: dla każdego x, jeżeli x jest kobietą, to x jest gadatliwa.

Zdanie ogólno twierdzące

• Niektóre kobiety są gadatliwe

Zdanie szczegółowo twierdzące

• Żadna kobieta nie jest gadatliwa.

Zdanie ogólno przeczące

• Niektóre kobiety nie są gadatliwe

Zdanie szczegółowo przeczące

• Tylko kobiety są gadatliwe

• Predykaty dwuargumentowe.

• Wszystko jest przyczyną wszystkiego

R9x, y): x jest przyczyną y

• Bóg jest przyczyną wszystkiego

• Istnieje coś, co jest przyczyną wszystkiego

• Wszystko ma swoją przyczynę

• Nic nie jest przyczyną niczego

• Język „J” nazywamy językiem pierwszego rzędu jeśli spełnia on następujące dwa warunki:

• słownik jego zawiera:

• nieskończenie wiele zmiennych indywidualnych, którymi są pewne litery reprezentujące przedmioty indywidualne z jakiegoś określonego zbioru i odpowiadającego nazwom jednostkowym owych przedmiotów

• przynajmniej jeden symbol relacyjny jest predykatem

• skończona liczbę spójników

• kwantyfikatory wiążące wyłącznie zmienne indywidułowe

• znaki techniczne tj. nawiasy (stałe nazwowe mogą ale nie muszą występować)

• Symboli należących do słownika języka „J” zgodnie z przyjętymi regułami gramatycznymi budujemy formuły, są nimi te ciągi wyrażeń ze słownika języka „J”, które są schematami poprawnie zbudowanych zdań jakiegoś języka etnicznego.

• Język klasycznego rachunku predykatów (KRP) wchodzą następujące grupy symboli

• zmienne indywidułowe (nazwowe) x1…xn…

• stałe indywidułwe a1…a2…

• symbole relacyjne (predykaty) P1…P2…

• spójniki zdaniowe ~^v -> ≡

• kwantyfikatory
  
  

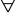
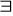
• znaki techniczne < > ( )

Argument:

N -> N

Argument (k) liczba argumentów predykatu Pk

P₁ Q₁ R₁ S₁

P Q R S

x ₁ y₁ z₁

x y z

a₁ b₁ c₁

a b c

• Wyrażenie - każdy skończony ciąg symboli ze słownika języka KRP nazywamy wyrażeniem tego języka.

• Atomowa formuła zdaniowa - formułą atomową języka KRP nazywamy dowolne wyrażenie postaci Pk(t1…t2)

gdzie Pk - n-argumentowym predykatem (n=Arg(k)), zaś t1...t2 - są dowolnymi termy

Formę języka KRP nazywamy dowolną zmianę lub stałą indywiduuową.

• Formuła atomowa

• wszystkie formuły atomowe są formułami języka KRP

• jeżeli A, B są dowolnymi formułami języka KRP to wyrażenia postaci:

~(A) (A)^(B) (A)v(B) (A) -> (B) (A) ≡(B)
(A)
(A)

• nie ma innych formuł języka KRP poza wymienionymi w punktach 1 i 2

• formułami są:

• formułami nie są:

• Zasięg kwantyfikatora - formułą A w formule
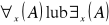
  nazywamy zasięgiem odpowiedzialnego kwantyfikatora.

^Zasięg

^Zasięg

Zasięg

Zasięg

• Zmienna związana i wolna. Dany egzemplarz zmiennej x występującej w formule A jest w niej związany, gdy albo występuje on w tej formule bezpośrednio po kwantyfikatorze, albo znajduje się w zasięgu kwantyfikatora wiążącego zmienną x, w przeciwnym przypadku egzemplarz zmiennej x jest wolny w tej formule.

zasięg

zasięg

zmienna

wolna

zmienna

związana

zmienna

związana

zmienna zmienna

związana związana

zmienna

wolna

zmienna

związana Formuły bez zmiennych wolnych

zmienna nazywamy zdaniami.

związana

13 Pojęcie tautologii KRP . Wybrane tautologie

• Tautologia KRP (formuła log. prawdziwa) nazywamy, formułą języka klasycznego rachunku predykatów, która jest prawdziwa przy dowolnym rozumieniu występujących w niej symboli relacyjnych (predykatów), stałych indywidualnych (nazw) i zmiennych indywidualnych.

• Tautologie KRP

Np. jeżeli wszyscy są leniwi to Zenek jest leniwy.

dictum de omni (przepowiedziane ze wszystkiego)

Np. Jeśli Zenek jest leniwy to istnieje ktoś, kto jest leniwy

dictum de singulo (przepowiadanie z pojedynczego)

Np. Jeżeli wszyscy są leniwi, to istnieje ktoś, kto jest leniwy.

np. jeżeli wszyscy są leniwi to istnieje ktoś, kto jest leniwy.

• Prawa de Morgana

• 
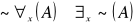
  negowania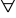
  

Np. nie wszyscy są altruistami wtw, gdy istnieje ktoś, kto nie jest altruistą

• 
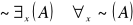
  negowania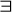
  

Np. nie istnieją altruiści wtw, gdy nikt nie jest altruistą

• 
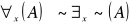
  zastępowania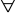
  

Np. wszyscy są altruistami wtw, gdy nie istnieje ktoś, kto nie jest altruistą

• 
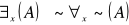
  zastępowania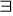
  

Np. Istnieje ktoś kto jest altruistą wtw gdy nie prawda że nikt nie jest altruistą.

• Prawa dotyczące przestawiania kwantyfikatorów

• 
  

Np. wszystko jest przyczyną wszystkiego wtw, gdy wszystko ma swoją przyczynę we wszystkim

• 
  

Np. istnieje ktos, kto ma przyjaciela. Istnieje ktoś, kto jest czyimś przyjacielem

• 
  prawo przestawiania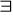
  z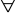
  

Np. jeżeli istnieje ktoś, kto zdobył każdy ośmiotysięcznik, to istnieje każdy ośmiotysięcznik, który został zdobyty przez kogoś.

• Prawa rozdzielności

• 
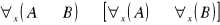
  prawo rozkładania dużego kwantyfikatora względem implikacji Np. każdy adwokat jest prawnikiem, to każdy prawnik jest adwokatem

• 
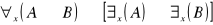
  prawo rozkładania małego kwantyfikatora względem implikacji

• 
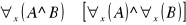
  prawo rozkładania dużego kwantyfikatora względem koniunkcji Np. Każdy człowiek jest ssakiem i kręgowcem, każdy jest ssakiem i kręgowcem

• 
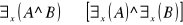
  prawo rozkładania małego kwantyfikatora względem koniunkcji

• 
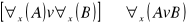
  prawo rozkładania dużego kwantyfikatora względem alternatywy Np. każdy polityk kłamie lub każdy polityk jest godzien szacunku, wszyscy kłamią lub wymagają szacunku

• 
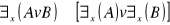
  prawo rozkładania małego kwantyfikatora względem alternatywy Np. istnieje coś, co jest kwadratowe lub istnieje coś, co jest okrągłe. Istnieje coś, co jest kwadratowe lub okrągłe.

16 rodzaje rozumowań : dowodzenie wyjaśnianie , sprawdzanie hipotez

• Rozumowania oceniamy z punktu widzenia ich poprawności logicznej. Natomiast argumentacje oceniamy jeszcze ze względu na ich skuteczność.

• Rozumowanie może służyć osiągnięciu następujących celów poznawczych:

• wzbogaceniu systemu wiedzy obiektywnej lub subiektywnej poprzez odwołanie się do zdań już należących do tego systemu

• może służyć podniesieniu wartości poznawczej danego zdania

ustalenie związków między tym, co już znane ( co wchodzi w skład naszej wiedzy

17 Pytania i odpowiedzi ( pojęcie pytania, rodzaje pytań , budowa pytania , założenie pytania , pytanie poprawnie postawione , rodzaje odpowiedzi .

Pytanie - To wyrażenie , które wskazuje na pewien brak wiedzy i wskazuje na dążenie do uzupełnienia tego braku

Rodzaje Pytań :

• pytanie rozstrzygające - jest to pytanie w postaci `' Czy A ? `' , Gdzie A jest dowolnym zdaniem w sęsie logicznym i na którą oczekiwaną odpowiedzią jest zdanie `' A `' lub jego negacja

• Pytanie dopełnienia - jest to pytanie ,m które po 1 zawiera partykuły pytania takie jak : i , kto , co , gdzie , kiedy , jak i po2 , które wyznacza kształt oczekiwanej odpowiedzi

• Pytanie zamknięte - wyznacza kształt oczekiwanej odpowiedzi

• Pytanie otwarte - nie wyznacza kształtu oczekiwanej odpowiedzi

• Pytania założeniowe - to takie , że dla A jest ono propozycją wszystkich odpowiedzi właściwych na to pytanie np. Czy przestałeś już bić swoją żonę ?

• Pytanie wyboru - Pytanie na które dany jest zbiór możliwych , oczekiwanych odpowiedzi . ( ( testy , Ankiety ) .

• Istnieje przynajmniej 1 odpowiedź prawidłowa na dane pytanie oddaje się za pomocą pozytywnego założenia

A	B	(A)v(B)
1	1	1
1	0	1
0	1	0
0	0	0

A	B	(A)^(B)
1	1	1
1	0	0
0	1	0
0	0	0

A	~(A)
1	0
0	1

A	B	(A)->(B)
1	1	1
1	0	0
0	1	1
0	0	1

A	B	(A) ≡ (B)
1	1	1
1	0	0
0	1	0
0	0	1




---