I NARZĘDZIA MENEDŻERA

Ekonomia, podobnie do innych nauk, wykorzystuje odpowiedni dla siebie zestaw narzędzi. Właściwe wykorzystanie tych narzędzi sprawia, że uzyskane informacje charakteryzują się dużą wiarygodnością, a analiza staje się czytelna. Warto dodać, że wspomniane narzędzia, w większości przypadków, zostały zapożyczone z dorobku nauk ścisłych (matematyka, fizyka, statystyka, informatyka).

W procesie badania gospodarki ekonomista dokonuje obserwacji procesów gospodarczych, a następnie uogólnia wyniki i formułuje wnioski. A więc, aby przeprowadzić wiarygodne badanie, nie wystarczy tylko odnotowanie zaistniałego faktu lub stwierdzenia jego powtarzalności w czasie. Potrzebne są również dane liczbowe, analiza których może prowadzić do wykazania ogólnych trendów zmian lub dokonywania porównań w czasie.

Indywidualne prowadzenie badań, oznacza zdobywanie danych „na własną rękę”, w obecnej rzeczywistości gospodarczej jest prawie niemożliwe. Wynika to głównie z ograniczonych możliwości technicznych i finansowych badacza. W tej sytuacji należy wykorzystać informacje z innych źródeł

Źródła danych

Z informacjami statystycznymi spotykamy się codziennie w mediach - w relacjach telewizyjnych, gazetach, itp. Większość z nich produkują rządy, przedsiębiorstwa i wiele innych organizacji. Są to opracowania urzędów statystycznych, ministerstw, banków, oraz instytucji podejmujących się odpłatnie przeprowadzaniem badania np. COBOP.

Również międzynarodowe instytucje takie jak Bank Światowy, Międzynarodowy Fundusz Walutowy, wyspecjalizowane organa ONZ czy np. OPEC udostępniają zebrane wyniki przeprowadzanych badań. Najwięcej informacji dostarcza Główny Urząd Statystyczny

Warto wspomnieć, że początki polskiej statystyki sięgają roku 1789; wtedy Sejm zarządził pierwszy ogólnokrajowy spis ludności i dymów (domów). Główny Urząd Statystyczny (GUS, natomiast,) jako państwowy naczelny organ statystyki został utworzony 13 lipca 1918 roku. Urząd funkcjonował do wybuchu drugiej wojny światowej, a głównym organizatorem GUS był L. Krzywicki. Po II wojnie światowej, w 1945 roku, został reaktywowany jako centralny organ administracji państwowej w zakresie statystyki. Jak wspomniano wcześniej, obecnie jest największym polskim źródłem informacji o gospodarce Polski i świata.

Działania Urzędu obejmują, przede wszystkim: prowadzenie statystycznych badań życia gospodarczego, społecznego i kulturalnego oraz opracowywanie i ogłaszanie wyników tych badań, inaczej mówiąc GUS gromadzi, analizuje, opracowuje i udostępnia setki statystyk. Przeprowadza, m.in., Narodowy Spis Powszechny Ludności i Mieszkań, czyli spis wszystkich ludzi oraz lokali znajdujących się w okresie przeprowadzania spisu na terenie kraju.

Poza tym, urząd statystyczny prowadzi Polską Klasyfikację Działalności, czyli  umownie przyjęty podział zbioru rodzajów działalności społeczno - gospodarczej realizowanych przez podmioty gospodarcze. GUS zajmuje się również ważnym dla przedsiębiorców rejestrem REGON (zbiorem informacji o firmach gospodarki narodowej).

GUS, zgodnie z ustalonym harmonogramem, publikuje w określonych odstępach czasowych (miesięcznych, kwartalnych, rocznych) dziesiątki i setki rozmaitych danych i wskaźników. Dzięki temu znamy, np., wartość Produktu Krajowego Brutto, wyniki finansowe firm, wskaźniki bezrobocia i inflacji, wysokość przeciętnego miesięcznego wynagrodzenia w gospodarce. Powyższe informacje powalają dokonać oceny sytuacji gospodarczej kraju oraz określić poziom rozwoju na tle innych państw świata.

Poza regularną publikacją całego szeregu danych i wskaźników, GUS przedstawia także wiele raportów dotyczących wybranych dziedzin naszego życia. Prowadzi, ponadto, badania naukowe w zakresie metodologii statystyki, publikuje, m.in., „Rocznik Statystyczny” oraz „Mały Rocznik Statystyczny”, „Wiadomości Statystyczne” i „Zeszyty Statystyki Polskiej”.

GUS zbiera, opracowuje i ogłasza wyniki badań w zakresie statystyki międzynarodowej, bierze udział w pracach organizacji międzynarodowych w dziedzinie statystyki.

Wiarygodnych i porównywalnych danych dostarcza także Europejski System Statystyczny, którego centrum stanowi Urząd Statystyczny Wspólnot Europejskich - Eurostat. Głównym celem Eurostatu jest opracowywanie i przekazywanie instytucjom wspólnotowym porównywalnych danych oraz niezbędnych informacji statystycznych. Urząd odpowiada także za przygotowywanie prognoz i analiz gospodarczych oraz współpracę z urzędami statystycznymi państw członkowskich. Eurostat podlega Komisji Europejskiej (władza wykonawcza w UE), a konkretnie Komisarzowi ds. Polityki Ekonomicznej i Monetarnej. Siedziba Urzędu znajduje się w Luksemburgu. 

Warto wspomnieć, że poprzednikiem Eurostatu była skromna komórka statystyczna przy Europejskiej Wspólnocie Węgla i Stali, utworzona w 1953 roku. Urząd zaczęto budować dopiero po utworzeniu Komisji Europejskiej w 1958 roku. Pod swoją obecną nazwą Eurostat istnieje od 1959 roku, a obecną podstawę prawną istnienia Urzędu stanowi artykuł 282 Traktatu Amsterdamskiego z 1997 roku nakładający na Wspólnotę Europejską obowiązek gromadzenia i opracowywania danych statystycznych.  Kierując się tym artykułem, w lutym 1997 r. Rada UE przyjęła w formie rozporządzenia tzw. prawo statystyczne. Dokument ten definiuje podział kompetencji między Eurostatem, a jego odpowiednikami w państwach członkowskich UE.

Obecnie, podobnie jak inne narodowe urzędy statystyczne, polski Główny Urząd Statystyczny (GUS) ma obowiązek dostarczać do Eurostatu dane według ujednoliconych zasad ich zbierania i opracowania. Dzięki zgromadzeniu danych w jednym miejscu, można dokonywać międzynarodowych porównań, jak również określać podstawowe wielkości statyczne dla Unii Europejskiej traktowanej jako jedność składającą się z 25 części całość.

Rodzaje danych i ich prezentacja

By opisać różnego rodzaju zdarzenia gospodarcze, przedstawić zachodzące między nimi zależności, obliczyć ich siłę ekonomiści wykorzystują tabele wykresy

Pozyskane dane liczbowe przyjmują dwojakiego rodzaju postać. Mogą być one danymi przekrojowymi lub szeregami czasowymi.

Dane przekrojowe

Jak sama nazwa wskazuje, przedstawiają strukturę badanego problemu. Podają, więc one uzyskane w danym czasie wartości tej samej zmiennej pogrupowane według przyjętej kategorii np. bezrobocie w określonych grupach wiekowych, stopa inflacji w określonych państwach itd.

Dane przekrojowe informują o strukturze zjawiska, np. podając wartości analizowanej zmiennej dla poszczególnych osób lub grup osób w pewny okresie. Zawiera je tablica poniżej

Szeregi czasowe

Prezentują wartości analizowanej zmiennej w kolejnych jednostkach czasu (miesiąc, kwartał, rok itd.) Przykład szeregu czasowego. Zebrane dane prezentowane są w dwóch formach - tabelarycznej i graficznej (wykresy)

Tabele

Tabelaryczne zestawienie danych służy ich uporządkowaniu i ułatwia korzystanie z nich. Bardzo ważnym elementem tablicy jest przy tym jej opis zawierający tytuł, informujący czytelnika, jakiego zjawiska dotyczą zebrane liczby oraz oznaczenie kolumn i wierszy. Przy pomocy tabel podaje się zarówno szeregi czasowe jak i dane przekrojowe.

Dane przekrojowe Struktura bezrobocia według wieku ( w %)

Wiek	XII 92	XII 93	XII 94	XII 95	XII 96	XII 97
15-24	34,6	34,4	34,6	34,5	31,2	30,7
25-34	29,7	28,5	27,7	27,0	27,3	27,9
35-44	24,7	25,2	25,3	25,2	25,8	26,4
45-54	9,2	9,8	10,7	11,3	13,3	13,3
pow 55	1,8	2,0	1,7	2,0	2,4	1,7

Bezrobotni w Polsce według poziomu wykształcenia i płci (w tys.) W dniu 30 czerwca 1992
Wyszczególnienie	Ogółem	Mężczyźni	Kobiety
Ogółem	2 296,7	1 076,3	1 220,4
Z wyższym	54,4	25,9	28,6
Średnim ogólnokształcącym zawodowym	165,5 512,6	32,0 463,7	133,5 380,6
Zasadniczym zawodowym	845,3	463,7	380,6

Szeregi czasowe Kurs marki niemieckiej w NBP ( w zł )

Data	Kurs
12. 1997	1,89
03. 1998	1,94
06. 1998	2,12
09. 1998	2,09
12. 1998	2,19
03. 1999	2,09
06. 1999	2,19
09. 1999	2,16
12. 1999	2,02
03. 2000	2,08
06. 2000	2,08

Wykresy

Inna formą prezentacji danych liczbowych zawartych w tabelach są wykresy. Do prezentacji wielkości absolutnych najczęściej stosuje się wykresy słupkowe natomiast do prezentacji struktury jakiegoś agregatu, aby pokazać, czyli proporcje, w jakich proporcjach dzieli się go na części składowe, by pokazać, jakie są udziały w całości poszczególnych części składowych agregatu najczęściej stosuje się wykresy kołowe zwana również tortowymi.

Wykres kołowy ( tortowy ) Wykres słupkowy, kolumnowy ( histogram )

Wykresy ilustrujące związki i zależności

Powiedzmy, że interesuje nas związek stopy inflacji i wysokości wolnorynkowego kursu dolara Jeśli mamy dwa szeregi czasowe, to możemy spróbować wykryć zależność odpowiadających im zmiennych.

Miesiące Stopa inflacji Kurs dolara Kurs dolara zł/$

Styczeń 5,0 A 3,0 8,0

Luty 6,0 B 3,5 7,5 J *

Marzec 7,0 C 4,0 7,0 I *

Kwiecień 8,0 D 4,5 6,5 H *

Maj 9,0 E 5,0 6,0 G *

Czerwiec 10,0 F 5,5 5,5 F *

Lipiec 11,0 G 6,0 5,0 E *

Sierpień 12,0 H 6,5 4,5 D *

Wrzesień 13,0 I 7,0 4,0 C *

Październik 14,0 J 8,0 3,5 B *

Listopad 15,0 K 9,0 3,0 A * Stopa inflacji

Grudzień 16,0 L 10,0

5 6 7 8 9 10 11 12 13

W celu uwidocznienia tego związku możemy sporządzić tzw. wykres punk­towy. Parom liczb, opisującym ich poziomy obu wielkości zaobserwowane w kolejnych miesiącach 1996 r., odpowiadają na wykresie punkty A, B, C, D itd. (to właśnie im wykres zawdzięcza swoją nazwę).. Jeśli jedna z nich rośnie, to druga też rośnie. I odwrotnie - jeśli jedna z nich maleje, druga zachowuje się w taki sam sposób.

Dla wyraźnego zaznaczenia charakteru i siły związku wszystkie leżące w układzie współrzędnych punkty połączyliśmy jedną linią ciągłą. Może to być linia prostą tak jak na rysunku linia prosta (mówimy wtedy o zależności liniowej), lub krzywa (wówczas zależność ma charakter nieliniowy). Liniowy charakter zależności wskazuje, że jest to zależność wprost proporcjonalna O sile tego związku informuje jej kąt kąta nachylenia.

Sporządzony powyżej wykres nie ujawnia charakteru zależności między zmiennymi. Patrząc nań, nie potrafimy rozstrzygnąć, co jest przyczyną, a co skutkiem Nie wiemy, czy im wyższy jest poziom inflacji, tym bardziej wzrasta nominalny kurs dolara, czy też odwrotnie, im wyższy jest wolnorynkowy kurs waluty amerykańskiej, tym szybciej rosną ceny. Obie hipotezy dają się uzasadnić. I tak zwolennicy pierwszej hipotezy mogą utrzymywać, że strach przed wzrostem cen powoduje ucieczkę od waluty polskiej i napędza popyt na waluty wymienialne, co z kolei sprawia, że kurs dolara wzrasta. Jednak inni mogą być zdania, że to raczej rosnący kurs dolara powoduje, iż towary kupowane przez przedsiębiorstwa za granicą są coraz droższe, co podnosi ogólny poziom cen w kraju. Można też twierdzić, że obie zmienne pozostają pod wpływem trzeciego czynnika i że to on właśnie jest przyczyną występowania odkrytej zależności. Innym wytłumaczeniem wzrostu obu wielkości może być fakt wzrostu ilości pieniądza w obiegu. Jeżeli w badanym czasie państwo, drukowało i wprowadzało do obiegu pieniądze, by skupować na masową skalę dolary, to z jednej strony podnosi to rynkową cenę waluty amerykańskiej, z drugiej zaś zwiększona ilość pieniądza w obiegu, co mogło być przyczyną wzrostu ogólnego poziomu cen.

Aby rozstrzygnąć, kto ma rację, niezbędne jest skonfrontowanie konkuren­cyjnych hipotez z rzeczywistością. Należy w tym celu dokonać ich weryfikacji logicznej i o ile jest to możliwe empirycznej. Dzięki takiemu podejściu ekonomiści odrzucają lub akceptują przyjęte wstępnie hipotezy. Istnieją sposoby wyznaczenie przebiegu linii najlepiej „dopasowanej" do położenia wszystkich zaobserwowanych punktów i przedstawienia ich w postaci syntetycznych wzorów. Dostarcza ich : matematyka, statystyka i ekonometria.

METODY I NARZĘDZIA MATEMATYCZNE

Początkujący ekonomiści, jeżeli nie są zbyt mocni w matematyce, mogą w niej widzieć sztuczną przeszkodę do poznania zjawisk ekono­micznych.

Jeżeli zawsze miałeś z nią złe doświadczenia. Jeżeli jesteś po dłuższej przerwie w nauce i zapo­mniałeś wszystko, co kiedyś umiałeś, przeczytaj tę część wykładu uważnie krok za krokiem. Zawarta tu wiedza pozwoli przyjrzeć się kilku zastosowa­niom matematyki w ekonomii. Przede wszystkim pokaże, jak pomocne w analizie ekonomicznej mogą być funkcje i równania. Przy ich pomocy można objąć zasięgiem analizy wszystkie ważne determinanty zmian badanej kategorii.

Równania

Dla ekonomisty zmienne i przedstawiające zależności miedzy nimi funkcje stają się naprawdę interesujące, dopiero wtedy, gdy możemy je przedstawić w postaci równań lub nierównościami algebraicznymi W tym miejscu zajmiemy się jedynie jednym z podstawowych pojęć matematyki równaniami.

Równaniem nazywa się warunek zapisany w postaci równości, nakładany na niewiadome obiekty matematyczne (liczby, macierze, funkcje, operatory itp.) W  zależności od natury niewiadomych obiektów mówi się o równaniach liczbowych np. X
= 9 równaniach macierzowych, np. równaniach funkcyjnych, np. f(x,y) = f(x) + f(y) i równaniach operatorowych.

Rozwiązanie równania

Wartość X, która je spełnia nazywa się rozwiązaniem równania. Równanie może mieć jedno lub wiele rozwiązań (również nieskończenie wiele), może też w ogóle nie mieć rozwiązania. Rozwiązać równanie oznacza znaleźć wszystkie jego rozwiązania. Weźmy dla przykładu następujące równania:

2X= 8 ; X
= 9 ; f (x) = 5.

Pierwsze z powyższych równań ma jedno rozwiązanie X= 4, drugie natomiast ma dwa X=3 oraz X=-3. Trzecie równanie jest po prostu równaniem ogólnym. Nie znamy rozwiązania, dopóki nie poznamy konkretnej reguły, którą oznacza f

Równaniem może mieć jedną lub więcej niewiadomych Równaniem o jednej niewiadomej x jest równość dwu funkcji f(x) = g(x), rozważanych we wspólnej dziedzinie. Równaniem o n niewiadomych x₁, x₂,..., x_n jest równość w postaci f(x_1, x₂,..., x_n) = g(x₁, x₂,..., x_n). Rozważa się również układy równań, np. m równań z n niewiadomymi.

W zastosowaniach ekonomicznych możemy rozróżnić dwa typy równań: równanie definicyjne, behawioralne

Równania definicyjne (ang. definitional equation)

Tego typu równania ustanawiają tożsamość dwu wyrażeń, które mają dokładnie ten sam sens. W takim równaniu często używany jest znak identyczności
(czytaj: jest zawsze identyczne, równe) zamiast zwykłego znaku równości =, chociaż ten ostatni również jest dopuszczalny.

Tożsamość jest zależnością między zmiennymi, która jest zachowana dla wszystkich wartości zmiennych. Oto przykład tożsamości:

(a+b)

a
+2ab + b
,

Specjalny symbol
oznacza, że lewa i prawa strona są równe dla wszystkich wartości zmiennych. Równanie jest zachowane jedynie dla nie­których wartości zmiennych, podczas gdy tożsamość jest prawdziwa dla wszystkich wartości zmiennych.

W ekonomii często tożsamość jest prawdziwa z mocy definicji wprowadzonych pojęć. Na przykład całkowity zysk Z jest definiowany jako nadwyżka całkowitego przychodu UC nad całkowitym kosztem KC, co możemy zapisać:

Z
UC- KC

Równania behawioralne (ang. behavioral equation)

Określa sposób, w jaki za­chowuje się zmienna w reakcji na przyrosty innych zmiennych. Może to dotyczyć albo zachowania ludzi (np. związki struktury zagregowanej konsumpcji z dochodem narodowym), albo innych jednostek (np. sposób, w jaki całkowity koszt reaguje na zmiany poziomu produkcji firmy). Szeroko rozumiane równania behawioralne mogą być używane do opisu ogólnych instytucjonalnych uwarunkowań modelu, obejmujących aspekty technologiczne (np. funkcja produkcji) i prawne (np. struktura podatków). Zapisanie równania behawioral­nego w postaci matematycznej jest zawsze poprzedzone przyjęciem określonych założeń dotyczących sposobu zachowania rozważanej zmiennej. Rozważmy dwie funkcje kosztu całkowitego:

KC=75+10*Q

KC= 110+Q

Gdzie Q oznacza ilość produktu, zaś KC koszt całkowity liczony w złotówkach

Równania te mają różną postać, opisują zatem różne warunki produkcji.. W pierwszym koszt stały, czyli wartość KC, gdy Q=0 jest równy 75, podczas gdy w drugim jest równy KC=110. Koszt zmienny jest również różny. W pierwszym dla każdego jednostkowego przyrostu wartości ΔQ=1 mamy jednakowy przyrost wartości ΔKC =10, w drugim natomiast w miarę jak Q wzrasta o kolejne jednostki, ΔQ=1 koszt całkowity będzie się zwiększał kolejno o coraz to większe ilości. ΔKC.

Wartości absolutne (bezwzględne)

W dalszych wykładach niekiedy odwoływać się będziemy do wartości absolutnych lub inaczej bezwzględnych Przypomnijmy zatem, że absolutną wartością liczby jest funkcja f (x) definiowana w następujący sposób:

x ,jeśli x > 0,

f (x)=

- x, jeśli x < 0.

Tak zatem absolutna wartość liczby może być znaleziona przez odrzucenie jej znaku. Absolutna wartość zmiennych funkcji jest zazwyczaj zapisywana jako |y |

Innym pożytecznym i często wykorzystywanym narzędziem są różnego rodzaju funkcje matematyczne.

Funkcje - czyli przedstawianie współzależności w sposób ilościowy

Analiza współzależności zachodzących pomiędzy różnymi kategoriami ekonomicznymi wymaga rozumowania funkcyjnego, którego doskonałym wyrazem jest matematyczne pojęcie funkcji. Z łaciny znaczy to tyle co odwzorowanie, przekształcenie. Jest to jedno z podstawowych pojęć wyrażające (w najprostszym przypadku) wzajemny związek lub zależność dwóch lub więcej wielkości. Mówiąc prościej funkcja to reguła, która opisuje zależność między liczbami. Dla każdej wartości zmiennej należącej do zbioru X, funkcja przypisuje zgodnie z jakąś regułą jedną i jedyną liczbę zmiennej Y. W zależności od sposoby podejścia, stosowane są funkcje jednoczynnikowe lub wieloczynnikowe

Ogólny zapis funkcji jednoczynnikowej

Często chcemy jedynie wskazać, że jakaś zmienna Y zależy od jakiejś innej zmiennej X, ale nie znamy lub nie chcemy przedstawić konkretnej algebraicznej postaci związku między tymi dwiema zmiennymi. W takim przypadku posługujemy się najbardziej ogólnym zapisem

Y= f(X),

Zapis taki jest to równoznaczne ze stwierdzeniem, że zmienna Y zgodnie z bliżej nieokreśloną regułą f zależy od X. Mówiąc prościej wielkość zmiennej Y jest w jakiś sposób uzależniona od poziomu zmiennej X.

Przy zapisie typu Y=f(X) element X nazywa się zmienną niezależną (endogeniczna),lub argumentem funkcji, a element Y — wartością funkcji, lub niekiedy (nieściśle) zmienną zależną od X (egzogeniczna). W zależności od sposoby podejścia, stosowane są funkcje jednoczynnikowe lub wieloczynnikowe

Funkcję można wskazać przez opisanie reguły. Na przykład „weź liczbę X i podnieś ją do kwadratu", lub weź liczbę X i pomnóż ją przez 2 itp. Te konkretne funkcje zapisujemy symbolicznie jako Y= X
, Y= 2*X. Przy takim zapisie możemy mówić funkcjach jako swojego rodzaju regułach transformacji, bo pokazują, jak jeden zbiór liczb liczby transformują się w drugie.

Funkcje wielu zmiennych

W rzeczywistości jednak niektóre zmienne ekonomiczne Y mogą być zależą od wielu innych zmiennych X1, X2..Xn. i tak dalej. Aby wskazać, że więcej zmiennych razem określają wartość Y. najogólniej zapisujemy to w postaci Y=f(X1, X2...Xn).

W ekonomii dobrym przykładem funkcji wielu zmiennych jest rynkowy popyt, czyli ilości Qd, które nabywcy skłonni są w jakimś okresie i miejscu kupować w zależności od bardzo wielu czynników. Zmian każdego z nich powoduje, że zmieniają się ujawnione na rynku chęci zakupów. Najważniejsze z nich to:

* cena danego dobra-C,

* ceny dóbr substytucyjnych (zamienników) - Cs,

* cena dóbr komplementarnych (uzupełniających) - Ck,

* budżet przeznaczony na wydatki- B,

* majątek jaki dysponują nabywcy- F,

* podatki oraz transfery -T, ilość kupujących- N,

* użyteczność danego dobra dla konsumentów-U,

* gusty i preferencje nabywców- G,

* oczekiwania (spekulacja)- E,

* czynniki losowe- L.

Funkcję tę (jej matematycznym odpowiednikiem są wielomiany) w najogólniejszej postaci możemy zapisać jak poniżej:

Qd=f (C, Cs, Ck, B, F. T, N, U, G, E, L)

Z przedstawionego zapisu wynika, że na wielkość zakupów wpływa zmiana każdej zmiennej niezależnej. Im więcej czynników, tym bardziej złożona postać funkcji, tym trudniej przedstawić jej matematyczną postać, nie mówiąc o jej ilustracji graficznej.

Przejście z funkcji wieloczynnikowej do jednoczynnikowej

Funkcją wieloczynnikową, w której uwzględnia się wszystkie brane pod uwagę czynniki jednocześnie posługujemy się gdy chcemy pokazać złożoność zjawiska popytu, chcemy podkreślić, że popyt, to są ilości dóbr, które nabywcy skłonni są kupić w zależności od wielu zmiennych występujących jednocześnie często współzależnych,

Dla ułatwienia analizy często wpływ każdego z nich badany jest przy założeniu, że wielkości pozostałych zmiennych nie ulegają zmianie czyli przy przyjęciu klauzuli ceteris paribus. Przyjęcie tego założenia oznacza że dla każdego czynnika możemy zbudować niezależną jednoczynnikową funkcję popytu, w której pozostałe czynniki stanowią wyraz wolny

Jeśli zatem chcemy operować łatwą do zapisania i wykreślenia w układzie dwuwymiarowym tylko jedną funkcją popytu, to ze wszystkich możliwych czynników musimy wybrać ten, który będzie miał w dalszej analizie rynku największe znaczenie. Tym podstawowym czynnikiem jest rynkowa cena analizowanego wyrobu. Siłą rzeczy wszystkie pozostałe znane nam czynniki zgodnie z zasadą ceteris paribus zawarte są w wyrazie wolnym Najogólniejszą postać takiej funkcji możemy zapisać jak poniżej

Qd = f (C) + ceteris paribus

Precyzyjne zapisania funkcji popytu w postaci równania np.:

Qd= 100- 4C

wymaga przeprowadzania odpowiednich badań rynku, zebrania danych i dopasowania do nich funkcji matematycznej. Pomaga nam w tym nauka statystycznej weryfikacji teorii ekonomicznych i prognoz, zwana ekonometrią. „Metria” oznacza tu pomiar uzyskanych dzięki statystyce zmiennych ekonomicznych oraz siły zachodząc między nimi zależności. Wykorzystując teorie ekonomiczną, dostarczone przez statykę dane liczbowe i oferowane przez matematykę metody, ekonometrycy konstru­ują testują i oferują ekonomistom modele ekonometryczne. Są to pojedyncze równania lub ich zestawy, które opisują zależności pomiędzy zmiennymi ekonomicznymi. Jednym z takich modeli jest przedstawiona w postaci matematycznego równania z oszacowanymi na podstawie danych statystycznych parametrami funkcja popytu rynkowego

Zmiany absolutne i stopy zmian

Zmiany

Zapis ΔX nie oznacza iloczynu Δrazy X Czytamy go, jako zmiana poziomu X. Jeśli X zmienia się z X0 do X1, to zmianą X jest po prostu

ΔX= X1- X0.

Podobnie odczytujemy zapis ΔY=Y1-Y0. Czasami wyrażamy to powiadając, że ΔX i ΔY przedstawiają zmiany krańcowe (marginalne).Są to przyrosty zmiennych, które mogą być dodatnie lub ujemne

Aby wskazać, że X1 jest równe X0 plus lub minus zmiana X możemy także zapisać:

X1 = X0 +/-ΔX

Gdy mamy do czynienia z bardzo (nieskończenie) małymi przyrostami obu zmiennych, zamiast symbolizującej zmiany dużej litery z greckiego alfabety Δ używamy małej litery δ

Stopa zmian

Stopa zmian ilustruje, jak zmienia się Y, gdy zmienia się X. Obliczamy ją jako stosunek przyrosty zmiennej zależnej ΔY do przyrosty zmiennej niezależnej ΔX.

ΔY δY

------ lub -------

ΔX δX

Stosunek ten w zależności od charakteru związku funkcyjnego może być: dodatni lub ujemny może przyjmować wartość zero lub nieskończoność ponadto może być stały lub zmienny

Praktyczne wykorzystanie matematyki w ekonomii polega na przekształcaniu równań w tabele oraz wykresy, które w ekonomii bez względu na ich kształt są zwana krzywymi. Ponieważ są one powszechnie stosowane musimy zatem nauczyć się konstruowania krzywych i poznać sposoby ich analizy

Tabele i wykresy funkcji

Przypuśćmy, że mamy równanie, które pozwala w liczbach wyrazić wartość Y odpowiadającą każdej wartości X. Takie opisujące zależności pomiędzy zmiennymi równanie można przedstawić posługując się tabelą lub wykresem, bądź jednym i drugim na raz.

Wykres jest graficznym przedstawieniem zależności występujących między dwoma lub więcej zmiennym ekonomicznymi. Wskazuje na pewne ich właściwości, a często ilustruje dość zawiłe, ilościowe związki przyczynowo - skutkowe. W najprostszym przypadku, kiedy zarówno X, jak i Y są liczbami, funkcję Y= f(X) można na ogół wykreślić istniejące miedzy nimi zależności w prostokątnym układzie współrzędnych. Ilustrujący ten związek wykres składa się z osi pionowej (rzędnych) i osi poziomej (odciętych). Punkt ich przecięcia stanowi początek układu współrzędnych, przypisujący każdej ze zmiennych wartość zero. W matematyce zmienną niezależną przedstawia się na osi poziomej X, a zmienną zależną na osi pionowej Y. Charakterystyczną cechą wykresów jest to, że na obu osiach mogą być odłożone różne jednostki pomiaru np. cena w złotówkach a ilości w mln sztuk/miesiąc. Poza tym odmienna może być również przyjęta na obu osiach skala.

Podstawowym atutem wykresów jest możliwość wizualnego przedstawienia na małej powierzchni znacznej ilości informacji, których treść staje się bardziej czytelna a interpretacja nie wymaga żmudnych opisów słownych. Zaletą wykresów jest to, że jeśli w układzie współrzędnych wybierzemy jakąkolwiek wartość X, to wystarczy spojrzeć na nią i natychmiast można odczytać wartość Y. Drugą niepodważalną zaletą krzywych jest to, że pozwala ona wizualnie, bez odwoływania się do liczb, określić nie tylko kierunek ale również siłę zależności pomiędzy zmiennymi.

Wykorzystywane w ekonomii funkcje i ilustrujące je wykresy mogą obrazować zależności jednokierunkowe, odwrotnie kierunkowe, mogą ilustrować przejście od jednych do drugich, czyli stany ekstremalne. Mogą to być funkcje ze stałym przyrostem (liniowe ) lub zxe zmiennym przyrostem (nieliniowe) Mogą również ilustrować sytuacje, w których analizowane wielkości są od siebie niezależne, czyli autonomiczne. Przyjrzyjmy się zatem bliżej najczęściej stosowanym w ekonomii funkcjom.

Funkcje ze stałym przyrostem (liniowe)

Jeżeli dana zmiana wielkości niezależnej ΔX=const powoduje zawsze takie same zmiany wielkości zależnej o ΔY=const, to mamy do czynienia z funkcją ze stały przyrostem, jej wykresem jest krzywa o stałym nachyleniu, czyli linia prosta. Jej nachylenie może być dodatnie lub ujemne.

Zależności jednokierunkowe

Zacznijmy od zależności jednokierunkowej Zależność tego typu ilustruje poniższa tabela i wykres.

Wykres funkcji Punkty Funkcja tabelaryczna

Y X ΔX Y ΔY ΔY/ΔX

Y1 E* A 0 - 0 - -

D* +ΔY B 1 1 10 10 +10

Y0 C * C 2 1 20 10 +10

B* +ΔX D 3 1 30 10 +10

A * α ) E 4 1 40 10 +10

X0 X1 X

W tabeli powyżej mamy zbiór punktów A, B, C, D, E przedstawiających różne wynikające z zależności miedzy zmiennymi kombinacje X i Y.. Jeżeli punkty te naniesiemy do układu współrzędnych, to ich zbiór stanowi wykres punktowy funkcji.

Jeżeli punkty te połączymy ze sobą, to otrzymamy liniowy wykres funkcji. W ekonomii linia ta, niezależnie od przyjmowanego kształtu, nazywana jest zawsze krzywą. Ponieważ obie analizowane zmienne ekonomiczne rosną bądź spadają równocześnie, analizowana krzywa ma nachylenie dodatnie, inaczej mówiąc jest rosnąca czyli ma nachylenie dodatnie .

Funkcję tę opisuje szczegółowe równanie Y=10 *X Oznacza ono, że gdy X zmienia się o jednostkę ΔX=1, to Y zmienia się o ΔY=10. Patrząc na to nieco inaczej równanie to opisuje sytuację, w której wartość Y jest zawsze 10 razy większa od wyznaczającej ją wartości X, co zapisujemy Y/X=10.

W naszym przykładzie wielkości X i Y zmieniają się skokowo ΔY=10 i ΔX=1. Są to zmiany dyskretne, zatem odległość między kolejnymi punkami zmienia się również w ten sposób. Oznacza to, że nasza krzywa składa się z określonej ilości skończonych odcinków łączących kolejne punkty Jest to zatem linia przerywana. Gdyby przyrosty zmiennych były nieskończenie małe ΔX-->0, oraz ΔY-->0, co zapisujemy symbolicznie jako δX i δY, wówczas odległość między punktami też byłaby nieskończenie mała, a ilość odcinków łączących poszczególne punkty byłaby nieskończenie duża. W tych warunkach nasza krzywa stała by się linią ciągłą

Przedstawiona powyżej linia ilustruje funkcję bez wyrazu wolnego , zatem rozpoczyna swój bieg w punkcie A, gdzie obie zmienne mają wartość równą zero.

Funkcja z wyrazem wolnym

Przypuśćmy, że nasza krzywa nie wychodzi z początku układu, lecz zaczyna swój bieg powyżej lub poniżej tego punktu. Co wtedy? Aby ją wykreślić musimy znać wartość Y, gdy wartość X=0. którą musimy uwzględnić w postaci dodatkowego członu w równaniu. Jest to tzw. wartość przechwycenia (intercepcji),

Rys. Wykres funkcji z wyrazem wolnym

Y Y=5+10*X Y=-2+10*X

Y=+5

0 X

Y=-2

Jeśli przyjmiemy, że wartość przechwycenia wynosi a=+5, to nasza funkcja przyjmie postać Y=5+10*X. Na wykresie przecina ona oś rzędnych powyżej początku układu na poziomie Y=5. Może się jednak zdarzyć, że wartość przechwycenia jest ujemna wynosi np. a=-2 Wtedy funkcję taką zapiszemy jakoY=-2+10*X. Na wykresie przecina ona oś rzędnych na poziomie Y=-2 natomiast oś odciętych na prawo od początku układu

Zależności odwrotnie kierunkowe

Jeżeli zmienne ekonomiczne zmieniają się w odwrotnych kierunkach, to znaczy wzrostowi wielkości zmiennej niezależnej towarzyszy spadek wielkości zmiennej zależnej , a spadkowi wzrost, mówimy o zależności odwrotnie kierunkowej. W takiej sytuacji, analizowana krzywa ma nachylenie ujemne inaczej mówiąc jest opadająca.

Z zamieszczonej poniżej tabeli wynika, że zawarte w niej dane można zapisać syntetycznie w postaci równania Y= -10 - 10*X

Wykres funkcji Punkty Funkcja tabelaryczna

Y X Y

A A 0 40

Y1 B B 1 30

-ΔY C C 2 20

Y0 D D 3 10

+ΔX E E 4 0

X0 X1 X

Uogólnione równania krzywej prostoliniowej przyjmuje postać

Y= a + b*X

Gdzie dodatni lub ujemny parametr a (wyraz wolny) wskazuje wartość funkcji gdy X=0. Przesuwa on ją równolegle w górę lub w dół w stosunku do funkcji bez wyrazu wolnego Natomiast człon b (współczynnik nachylenia) w zależności od znaku pokazuje, czy jest to zależność jednokierunkowa czy odwrotnie kierunkowa. Jednocześnie mierzy on nachylenie funkcji

Nachylenie linii prostych

Indywidualną właściwością każdej krzywej jest jej nachylenie. Trygonometryczną miarą nachylenia linii prostej w dowolnym punkcie jest tangens kąta jej nachylenia względem osi odciętych

Rys Nachylenie linii prostej

tgα=ΔY/ΔX

Y B

Y1 B`

A α) ΔY

Y0 ΔX

α) X

X0 X1

Możemy je policzyć na dwa sposoby. Możemy posługiwać się przyrostami, czyli stopą zmian. I tak nachylenie na odcinku AB mierzy tg=ΔY/ΔX. W drugim odwołujemy się do wielkości całkowitych. W dowolnym punkcie krzywej jest ono identyczne i wynosi:

tgα =YA/XA

W obu przypadkach kąt nachylenia α jest taki sam, zatem na zasadzie podobieństwa trójkątów oba liczone różnymi sposobami tangensy muszą być sobie równe.

Nachylenie na łuku i w punkcie

W przedstawionym powyżej przykładzie stały wzrost zmiennej niezależnej o 10 jednostek powoduje stały przyrost zmiennej zależnej o 10 jednostek. Mamy dzięki temu wielkość nachylenia równą 1. Liczone metodą stosunku przyrostów (stopy zmian) ΔY/ΔX nachylenie linii prostej jest zawsze stałe. Gdy wyznaczające długość odcinka (przeciwprostokątna) punkty zaczniemy przybliżać do siebie np. do rozmiarów odcinka A B` wówczas boki przyprostokątne trójkąta także ulegną zmniejszeniu. A ponieważ zmniejszają się one proporcjonalnie, kąt nachylenia α pozostanie taki sam. Nie zmieni się również w sytuacji, w której przy nieskończenie małych przyrostach δX i δY punkty te przybliżą się do siebie na tak małą odległość, że zleją się i stworzą jeden punkt na krzywej.

Stałość nachylenia linii prostych nie oznacza jednak, że wszystkie linie proste mają identyczne nachylenia. Jego wartość określona jest przez stosunek ΔY/ΔX. Im jest on większy, tym krzywa jest bardziej stroma, im mniejszy, tym linia ta jest bardziej płaska. Jeżeli stałe zmiany zmiennej niezależnej o 10 jednostek powodować będą np. stałe zmiany zmiennej zależnej o 20 jednostek nachylenie będzie wynosić nie jeden a dwa.

Nachylenie 2/1 Nachylenie 1/2

Y Y

40

ΔY

α)

20 ΔX

10

5

α) X X

10 20 10 20

Zmienne niezależne (autonomiczne)

Istnieje wiele przypadków, w których jedna zmienna jest niezależna od drugiej. Oznacza to, że bez względu na to jak zmienia się wartość jednej, druga pozostaje bez zmian. Przykłady takich zależności obrazują zamieszczone poniżej wykresy przedstawiające linie poziome lub pionowe.

Rys A Rys B

Y Y

ΔY Y1 ΔY

Y0 ΔY=0 tgα = ------= 0 ΔX=0 tgα =-----=

ΔX Y0 ΔX

X

X0 X1 X0

Rysunek A może ilustrować zależność miedzy ilością dni słonecznych w Kalifornii X a wielkość zbiorów winogron we Francji Y. Nachylenie takiej funkcji jest równe zero

Z kolei rysunek B może przedstawiać zależności a raczej brak zależności pomiędzy poziomem ceny a ilością narkotyku zakupowego przez osobę uzależnioną, czyli tzw ćpuna Narkoman musi, jest zatem jest nieczuły na zmiany ceny. Nachylenie jego krzywej popytu jest nieskończenie duże

Funkcje odwrotne

W ekonomii (w odróżnieniu od wykresów matematycznych) często wykreśla się funkcje odkładając zmienne niezależne na osi pionowej, a zależne na osi poziomej. Z matematycznego punktu widzenia jest to funkcja odwrotna

Rys Funkcja popytu C Q

Cena 11 0

11 10 1

9 2

8 3

.

( α Kupowane ilości Qd 0 11

11

W ekonomii funkcje odwrotne wykorzystywane są do ilustracji zjawiska popytu i podaży. Jeżeli np. funkcja popytu przyjmuje postać C= a - b*Qd , gdzie a i b to wielkości stałe, to jej wykresem jest linią prostą, o stałym ujemnym nachylenie tgα=-b.

Często jednak analizowana krzywa ma zmienne nachylenie czyli jest wypukła na zewnątrz bądź w kierunku początku układu współrzędnych. W tej sytuacji mamy do czynienie z funkcją ze zmiennym przyrostem.

Funkcje ze zmiennym przyrostem

W ekonomii, technice i w ogóle w życiu często spotykamy sytuacje, gdy stałej zmianie wielkości niezależnej towarzyszą coraz większe lub coraz mniejsze przyrosty zmiennej zależnej. Mamy wówczas do czynienia z funkcjami ze zmiennymi przyrostami, lub, co na jedno wychodzi, z funkcjami o zmiennym nachyleniu. Oto przykład funkcji z rosnącymi skokowo przyrostami, czyli funkcji o rosnącym nachyleniu

Funkcja z przyrostem rosnącym

Wyobraźmy sobie, że analizowana firma zatrudnia kolejno coraz lepszych pracowników, co owocuje jak przedstawiono poniżej w tabeli coraz większym przyrostem produkcji ΔY towarzyszącym wzrostowi zatrudnienia o jednostkę ΔX= 1 W tej sytuacji mamy do czynienie z funkcją z rosnącym przyrostem

Rys . Funkcja z przyrostem rosnącym

Y

X	ΔX	Y	ΔY	tg α = ΔYΔ/X
0	-	0	-	-
1	1	2	2	2
2	1	5	3	3
3	1	9	4	4
4	1	14	5	5

1 2 3 4 X

Funkcja z przyrostem malejącym

Poniżej zamieszczamy z kolei przykład funkcji z malejącym skokowo przyrostem, czyli funkcji o malejącym nachyleniu. Wyobraźmy sobie, że firma zatrudnia kolejno coraz gorszych pracowników (zmienna X). Efektem dodatkowego zatrudnienia o ΔX=1 są coraz mniejsze przyrosty produkcji ΔY. Ponieważ przyrosty są wielkości skończone (dyskretne) wykresem funkcji jest linia łamana, Gdyby przyjąć, że analizowane przyrosty są nieskończenie małe, wykresem funkcji byłaby linia ciągła.

Rys Funkcja z przyrostem malejącym

Y

12

9

5 



0 1 2 3 X

Zmienne, których wielkości osiągają ekstrema.

Często się zdarza, że przyrosty funkcji zmieniają się z dodatnich na ujemne lub na odwrót. Zanim do tego dojdzie ich wartości bezwzględne stopniowo spadają. Gdy przyrost funkcji osiąga wartość zerową zmienia ona nachylenie zerowe. Jednocześnie osiąga ona maksymalny lub minimalny poziom, czyli inaczej mówiąc funkcja znajduje się w ekstremum.

Matematyczny zapis takie funkcji wyraża np. formuła równania kwadratowego o ogólnej postaci y= ax
+bx+c. Jej graficzną ilustracją jest parabola.

Rys A Funkcja z maksimum Rys B Funkcja z minimum

Y Y

Y0

Y=max

Y1

Y1

Y0

Y=min

X0 X1 Xopt X X0 X1 Xopt X

Ekstremum funkcji jest pojęciem bardzo przydatnym w ekonomii. W analizach zachowań podmiotów gospodarczych przyjmuje się, że mają one swoje możliwe do syntetycznego zapisania cele, które starają się w danych warunkach zmaksymalizować lub zminimalizować. Dla konsumenta celem tym będzie osiągnięcie maksymalnego zadowolenia (użyteczności całkowitej) z przeznaczonych na wydatkowanie środków pieniężnych. Celem producenta może być maksymalizacja zysków lub nie jest w stanie ich osiągnąć minimalizacja strat. Stąd też ekonomiści często wykorzystują w swych teoriach funkcje, które osiągają minimum lub maksimum.

Dobrym przykładem jednoczynnikowej funkcji z minimum jest zależność pomiędzy szybkością jazdy X a zużyciem paliwa na 100 km Y.

Z kolei przykładem dwuczynnikowej funkcji z maksimum jest wyprowadzona z ujemnie nachylonej funkcji popytu (gdy cena rośnie, kupowane ilości maleją i na odwrót) funkcja utargu całkowitego UC=Q*C liczonego jako iloczyn ceny C i sprzedanych ilości Q Hipotetyczne wielkości przedstawia zamieszczona poniżej tabela

Sprzedaż (Q)	Cena ( C)	Utarg całkowity (UC)=Q*C
0	11	0*11= 0
1	10	1*10= 10
2	9	2*9 = 18
3	8	3*8 = 24
4	7	4*7 = 28
5	6	5*6 = 30
6	5	6*5 = 30
7	4	7*4 = 28
8	3	8*3 = 24
9	2	9*2 = 18
10	1	10*1= 10
11	0	11*0= 0

Zawarte w niej wielkości można, jak to zrobiono nanieść do układu współrzędnych. W ten sposób otrzymujemy wykres funkcji utargu całkowitego.

Rys. Krzywe popytu rynkowego D i utargu całkowitego UC

C, UC

UC=max=30

Cp

D

C=5

D

0 1 2 3 4 5 6 7 8 9 10 11 Q

Z tabeli i ilustrującego ją wykresu wynika, że, gdy cena spada a sprzedane ilości rosną, to utarg całkowity najpierw rośnie. Przy cenie C=5 i 6 oraz odpowiadających im ilościach Q=5 i 6 osiąga wartość maksymalną, a następnie maleje do zera.

Funkcje z punktem przegięcia

Wyobraźmy sobie sytuację, w której wzrostowi jednej wielkości towarzyszy najpierw coraz większy przyrost (rosnące nachylenie funkcji) potem coraz mniejszy (malejące nachylenie), by w końcu z dodatniego zmienić się na ujemny. Zależności te przedstawia zmieszczona niżej tabela

Rys. Krzywa Knight`a

Produkcja X Lx X ΔX/ ΔLx

0 0 0

1 1 1

2 3 2 rosnący

3 6 3

4 10 4 max

5 13 3

6 15 2 malejący

7 16 1

Produkt krańcowy 4 8 Lx 8 16 (max) 0 zerowy

ΔX/ ΔLx 9 15 -1 ujemny

10 13 -2

Ilość zatrudnionych Lx

4 8

Ilustracją graficzną zawartych w tabeli danych jest funkcja z punktem przegięcia. W ekonomii krzywa ta zwana również krzywa Knight`a od nazwiska jej twórcy amerykańskiego ekonomisty Franka Knight`a (1885-1972). Jest ona również znana jako krótkookresowa funkcja produkcji. Ilustruje ona jedno z najważniejszych praw mikroekonomicznych, zwane prawem nieproporcjonalnych przychodów z czynnika zmiennego.

Nachylenie linii ciągłych ze zmiennym przyrostem

W przypadku funkcji z nieskończenie małymi przyrostami zmianom zmiennej niezależnej δX towarzyszą nieskończenie małe zmiany zmiennej zależnej δY.

Rys.A Rys. B

Y Y

60 b b

40 b`

ΔY

a α a α`

30 ΔX

X α`` X

20 30 20 25 30

Gdy nachylenie jest zmienne (linia wygięta) możemy mieć do czynienia z krzywą wypukłą względem początku układu współrzędnych lub krzywą wypukłą na zewnątrz układu W zależności od tego czy mamy do czynienia ze zmianami dyskretnymi, czy nieskończenie małymi mierzymy na łuku lub w punkcie.

Spróbujmy najpierw obliczyć nachylenie krzywej na rysunku A na skończonym odcinku miedzy punktami a b Przy przejściu z jednego punktu do drugiego występują mierzalne różnice ΔY i ΔX. Aby obliczyć nachylenie na tym odcinku, (czyli na łuku), łączymy oba punktu linię prostą Tangens kąta tej linii, czyli stosunek przyrostu zmiennej zależnej ΔY do przyrostu zmiennej niezależnej ΔX. jest miarą nachylenia naszej linii ale tylko na tym odcinku W naszym przykładzie nachylenie krzywej na odcinku a b wynosi tgα = ΔY/ΔX czyli (60 - 30)/(30 - 20) = 30/10 = 3

Coraz mniejszym przyrostom ΔX towarzyszyć będą coraz mniejsze przyrosty ΔY, zatem odległość między punktami a i b będzie się zmniejszać. W sytuacji, gdy przyrosty będą nieskończenie małe, co zapisujemy symbolicznie jako δX i δY, odległość między punktami a i b zmniejszy się do tego stopnia (stanie się nieskończenie mała), że zleją się one tworząc właściwie jeden punkt oznaczony na rysunku poniżej literą c. Miarą nachylenia funkcji w tym punkcie jest tangens kąta nachylenia linii proste stycznej do niej w tym punkcie) tgα=δy/δx

Rys A Funkcja wypukła na zewnątrz Rys B. Funkcja wypukła względem początku układu

Y Y

c c

d d

(α (α X (α (α X

Zwróćmy w tym miejscu uwagę na dość istotny szczegół, a mianowicie, że położenie stycznej względem funkcji wskazuje nam na jej kształt. Jeżeli styczna przylega do krzywej powyżej jej wykresu, co ilustruje powżej rys A, matematycy powiedzą, że mamy do czynienia z funkcją wypukłą na zewnątrz układu współrzędnych. Jej nachylenie jest rosnące większe w punkcie d niż w punkcie c. Jeżeli zaś przylega do niej poniżej jej wykresu, mamy do czynienia z funkcją wklęsła względem początku układu współrzędnych. O krzywej takiej mówi się potocznie, że jest wklęsła, jej nachylenie jest malejące mniejsze w punkcie d niż w punkcie c

Ruch wzdłuż krzywych a przesunięcia krzywych

Ruch po krzywej

Jeżeli analizujemy wpływ zmiennej niezależnej w modelu na zmienną zależną, to poruszamy się wzdłuż wykreślonej krzywej. Jeżeli jednak chcemy na wykresie uwzględnić również wpływ czynników innych, aniżeli przedstawiona na wykresie zmienna niezależna, to następuje przesunięcie wykreślonej krzywej w prawo bądź w lewo.

Zilustrujmy to na przykładzie popytu na parasolki. Zależność tą można najprościej wytłumaczyć w następujący sposób. Jeżeli cena rośnie, zaś ilość stojących do dyspozycji nabywców pieniędzy pozostaje niezmieniona, mogą oni kupić mniej parasolek, zatem kupowane ilości najprawdopodobniej zmniejszą się. Jeżeli natomiast ceny spadają, to kupowane ilości rosną.

Analizując zatem wpływ tylko jednej zmiennej niezależnej (ceny) na zmienną zależną (ilości) poruszamy się wzdłuż krzywej popytu w górę (jeżeli chcemy pokazać efekty wzrostu cen) lub w dół (jeżeli uwidaczniamy konsekwencje spadku cen). Popyt jest w ekonomii prezentowany w postaci funkcji odwróconej, zatem na os odciętych odkładamy ilości, a na osi rzędnych ceny

Rys. Ruch po krzywej

Cena Cena C IlościQ0

11 0 A

10 1 B

9 C 9 2 C

8 3 D

7 4 E

6 F 6 5 F

Ilości Q 5 6 G

2 5

Zaprezentowane poniżej funkcja popytu, przedstawiona została z przyjęciem założenia, że wszystkie pozostałe czynniki są niezmienione, co określane jest mianem klauzuli ceteris paribus.

W rzeczywistości kupowane ilości Q są uzależnione również od wielu pozacenowych czynników. Ilości Q mogą się zmieniać np. pod wpływem zmian wysokości dochodów, zmian indywidualnych gustów nabywców, mogą być również uzależnione od zmian warunków klimatycznych. Jeżeli np. ilość dni z opadami w danym roku wzrosła w porównaniu z latami ubiegłym, to kupowane przy każdym poziomie ceny „C” ilości parasolek wzrosną jak na przykładzie poniżej z Q0 do Q1.

Przesuwania krzywej

Aby uwzględnić ten pozacenowy czynnik w naszym modelu popytu, przesuwamy odpowiednio całą funkcję popytu:

* w prawo, gdy powodują on wzrost kupowanych ilości przy danych poziomach cen

* w lewo, gdy pod jego wpływem kupowane ilości zmniejszają się .

Rys Przesunięcia krzywej

Cena

9 c

7 e

Q

• 4 6

Przecinanie się krzywych

W ekonomii posługujemy się często modelami, w których zestawiamy i porównujemy ze sobą w jednym układzie współrzędnych dwie lub więcej funkcji. Szczególnie interesować nas będzie, jakie warunki muszą być spełnione, by obie funkcje jednocześnie przyjmowały te same wartości. Najbar­dziej znane w ekonomii warunki równowagi to równowago popytu i podaży:

Popyt Qd = Qs Podaż

Graficznie równowagę ilustruje przecinanie tworzących model funkcji Oto kilka przykładów ułożenia krzywych w układzie współrzędnych, w których nie dochodzi do ich przecięcia. Mówiąc inaczej na obu krzywych nie ma takich wielkości zmiennej niezależnej X, przy których obie funkcje mogą mieć równą wartości Y

Y Y Y

X X X

A oto przykłady ułożenia krzywych, przy których dochodzi do ich przecięcia się w punkcie oznaczonym literą E W punkcie tym wielkości zmiennych niezależnych Xe są dla obu funkcji identyczne podobnie wielkości zmiennych zależnych przyjmują w obu funkcjach identyczne wartości Ye.

Rys A Rys B

Y

D S E

Ye

Ye E

Xe X Xe X

Ekonomistę interesować będzie ponadto, a może przede wszystkim, jaki prawa i mechanizmy w analizowanym modelu ekonomicznym prowadzą do ukształtowania się identycznych wielkości w stosowanych w modelu funkcjach.

Zadanie

Przyjmiemy, że funkcja popytu na pszenicę Qd jest określona wzorem: Qd=700- 4*Cx, a funkcja podaży pszenicy Qs =100+ 2*Cx. Ile wynoszą: cena i ilości równowagi rynkowej?

Rozwiązanie

W warunkach równowagi Qs= Qd

100+2C= 700-4C

6C= 600

C=100zl/q

Qs=100+200= 300

Qd= 700- 400= 300

A teraz przyjmijmy, że rząd ustanawia minimalną cenę pszenicy na poziomie Cx.=120 zł za kwintal i jest zdecydowany kupować i magazynować powstałe nadwyżki. Ile kwintali pszenicy rząd będzie musiał skupić przechowywać i ile wyniosą dopłaty do produkcji pszenicy?

Rozwiązanie

Qd=700-4x120zł/q=220 Qs=100+2x120/q=240

Rząd musi skupić nadwyżkę podaży nad popytem Qs-Qd i zapłacić za nie ustaloną cenę

Qs-Qd= 220q-240q=20q*120zł/q= 2400zł.

Funkcje pochodne

W analizach ekonomicznych często wykorzystywane są funkcje pochodne Jest to jedno z podstawowych pojęć rachunku różniczkowego.

Niech y = f(x) oznacza funkcję ciągłą i określoną w przedziale (a, b); jeśli argumenty x oraz x + Δx (Δx — przyrost) należą do przedziału (a, b) i jeśli istnieje granica [f(x + Δx) - f(x)]/Δx, to granicę tę nazywa się pochodną funkcji f(x) w punkcie x i oznacza symbolem f '(x) lub df(x)/dx; wyrażenie [f(x + Δx) - f(x)]/Δx nazywa się przy tym ilorazem różnicowym, a pochodną df(x)/dx ilorazem różniczkowym. Geometrycznie pochodna funkcji f(x) przedstawia nachylenie stycznej, czyli tangens kąta α, który styczna do wykresu funkcji y = f(x) w punkcie P (x, f(x)) tworzy z dodatnim kierunkiem osi odciętych (osi x-ów). W różnych punktach pochodna f '(x) może mieć różne wartości, a więc odpowiadająca jej styczna do wykresu — różne nachylenia względem osi odciętych.

Do przedstawienia tej ważnej matematycznej kategorii wykorzystamy pojecie utargu krańcowego, które wyprowadzimy z utargu całkowitego. Przedtem parę definicji.

Utarg całkowity przeciętny i krańcowy

Przychód (utarg)całkowity UC (ang. total revenue-TR) jak pamiętamy jest to wartość sprzedanych przez firmę produktów. Obliczamy go mnożąc sprzedaną ilość Q przez ich cenę rynkową C.

UC= C * Q

Jeśli zbiór wartości utargów całkowitych i sprzedawanych ilości i cen naniesiemy na układ współrzędnych, to otrzymany wykres funkcji utargu całkowitego względem tych dwóch zmiennych

Przychód (utarg) przeciętny Up (ang. average revenue- AR) lub inaczej utarg jednostkowy, to iloraz przychodu całkowitego i wielkość sprzedanej produkcji Q

UC Q*C

Up = ------- -=-------- = C

Q Q

Utarg (przychód) krańcowy Uk (ang. marginal revenue- MR) to przyrost przychodów całkowitych ΔUC wywołany wzrostem sprzedaży o ΔQ. Obliczamy go dzieląc przyrost utargu całkowitego przez przyrost sprzedanych ilości:

ΔUC UC - UC₀

Uk= --------- = ---------------- = tg α

ΔQ Q₁ - Q₀

Gdy przyjmiemy, że ΔQ=1 wówczas Uk=ΔUC

Utargi krańcowe tworzą funkcję pochodną

Obliczane jako różnice utargu całkowitego wartości utargu krańcowego tworzą zbiór liczb zależnych od poziomu utargu całkowitego.

Jeśli miedzy zmiennymi całkowitymi UC i krańcowymi Uk zachodzi, zależność funkcyjna, to funkcja wielkości krańcowych w tym przypadku utargu krańcowego Uk=ΔUC/ΔQ określana jest jako pochodna względem funkcji całkowite (utargu całkowitego)

Naniesiony na układ współrzędnych zbiór liczb przedstawiających różnice tworzy wykres funkcji pochodnej od funkcji utargu całkowitego.

Utarg całkowity to suma utargów krańcowych

Operację obliczania różnic dla zmiennych skokowych (dyskretnych) w matematyce nazwa się różnicowaniem, a dla zmiennych ciągłych różniczkowaniem. Znając wartości różnic, czyli utargów krańcowy możemy bez trudu ustalić wartość utargu całkowitego Wystarczy je ze sobą zsumować

UC= ∑Uk

Operacja dodawanie do siebie tych różnic w celu uzyskania wielkości całkowitych nazywana jest w matematyce całkowaniem

Utarg całkowity przeciętny i krańcowy w warunkach stałej ceny

Przyjmijmy, że firma jest w stanie sprzedawać dowolną wielkość wytwarzanej produkcji, po jednej cenie C=const za sztukę Jej funkcję utargów całkowitych opisuje równanie

UC= C*Q

Przyrost utargu całkowitego ΔUC wynikać może w praktyce z przyrostu ceny ΔC z przyrostu ilości ΔQ, albo z przyrostu obu tych wielkości jednocześnie

Przyrost utargu całkowitego ΔUC obliczmy jako różnicę miedzy utargiem całkowity po zmianie ilości i ceny UC1=Q₁*C₁ a utargiem całkowitym przed jej zmianą UC0= Q₀*C 0

ΔUC= UC1-UC0 = Q₁* C1- Q0*C0

A ponieważ Q₁ =Q0+ΔQ, zaś C₁=C0 +ΔC, zatem wyrażenie UC1 możemy przedstawić jako:

UC₁= (Q0+ΔQ)*(C0+ΔC)

a po przemnożeniu wyrażeń zawartych w nawiasach otrzymujemy

UC1=Q₀* C₀+Q₀*ΔC+ΔQ*C₀ + ΔQ*ΔC

Przyrost utargu całkowitego możemy obecnie przedstawić jako różnicę:

ΔUC = (Q₀*C₀+Q₀*ΔC+ΔQ*C+ΔQ*ΔC) - Q₀*C₀

która po uproszczeniach przyjmuje postać:

ΔUC = Q*ΔC+ΔQ*C+ΔQ*ΔC

W naszym przykładzie firma sprzedaje dowolną wielkość swojej produkcji po stałej cenie, Gdy C=const , to ΔC= 0,oznacza to, ze przyrost utargu całkowitego jest wyłącznie wynikiem wzrostu sprzedanych ilości, czyli ΔUC= ΔQ*C.

Każda dodatkowo sprzedana jednostka ΔQ=1 daje zatem firmie przyrost utargu całkowitego ΔUC, czyli utarg krańcowy Uk równy:

ΔUC ΔQ * C

Uk = ------- = ------------- = C

ΔQ ΔQ

Wynika z tego, że gdy cena jest stała utarg krańcowy jest stały i równy cenie.

Poniższa tabela przedstawiają hipotetyczne zależności pomiędzy sprzedanymi ilościami Q utargami całkowitymi UC, przeciętnymi Up i utargami krańcowymi

Hipotetyczny przykład utargów w warunkach stałości ceny zbytu
Q	ΔQ	C= const	Utarg całkowity UC= ∑Uk	Utarg przeciętny Up= UC/Q	Przyrost utargu ΔUC=UC1- UC0	Utarg krańcowy Uk=ΔUC/ΔQ
0		10	0			-
1	1	10	10	10	10	10 - 0 =10
2	1	10	20	10	10	20 - 10=10
3	1	10	30	10	10	30 - 20=10
4	1	10	40	10	10	40 - 30=10

Przedstawione w tabeli wielkości i zachodzące między nimi zależności można przedstawić w postaci zamieszczonych wykresów funkcji

Rys Utarg całkowity przeciętny i krańcowy firmy

UC

UC

UC1

ΔUC

UC0 α)

ΔQ

α)

Q0 Q1 Q

Uk

Uk=ΔUC/ΔQ= C

Q0 Q1 Q

Ponieważ utarg krańcowy jest stały i dodatni krzywa utargu krańcowego jest linią prostą poziomą o stałym nachyleniu równym ΔC=0 Utarg całkowity otrzymujemy sumując otrzymane przez firmę utargi krańcowe UC= ΣUk. Krzywa utargu całkowitego jest zatem linia prostą o nachyleniu dodatnim równym wartości utargu krańcowego, czyli ceny

Utarg całkowity przeciętny i krańcowy w warunkach spadającej ceny

A teraz weźmy dla przykładu sytuację, w której firma, gdy chce sprzedać większe ilości., musi obniżyć cenę. Zależności pomiędzy hipotetycznymi ilościami cenami a wielkością utargu całkowitego przeciętnego i krańcowego przedstawia zamieszczona poniżej tabela.

Q	C	Utarg całkowity (UC)=Q*C	Utarg przeciętny Up=UC/Q	Utarg krańcowy Uk= ΔUC/ΔQ
0	11	0*11= 0	-	-
1	10	1*10= 10	10	10 - 0 = 10
2	9	2*9 = 18	9	18 - 10 = 8
3	8	3*8 = 24	8	24 - 18 = 6
4	7	4*7 = 28	7	28 - 24 = 4
5	6	5*6 = 30	6	30 - 28 = 2
6	5	6*5 = 30	5	30 - 30 = 0
7	4	7*4 = 28	4	28 - 30 = -2
8	3	8*3 = 24	3	28 - 24 = -4
9	2	9*2 = 18	2	18 - 24 = - 6
10	1	10*1= 10	1	10 - 18 = - 8
11	0	11*0= 0	0

Wszystkie przedstawione w tabeli wielkości można, jak to zrobiono na rysunku powyżej, wprowadzić do układu współrzędnych. W ten sposób zależności pomiędzy nimi przedstawimy przy pomocy wykresu interesujących nas funkcji

Rys. Krzywe popytu rynkowego utargu całkowitego przeciętnego i krańcowego

C, UC ,Uk

UC=max=30

Cp=11

D

C=5

0

Q=6 Uk Qa =11 Q

Z tabeli wynika, że funkcję popytu rynkowego przedstawia linia prosta o stałym nachylenie o ujemnym ΔC/ΔQ.

Przecina ona oś rzędnych przy cenie Cp=11, którą określa się jako prohibicyjną, gdyż przy takim poziomie ceny, wielkość popytu spada do zera. Krzywa ta przecina oś odciętych w punkcie, dla którego wielkość Qa=11 odpowiada poziomowi sprzedaży, przy której rynek jest nasycony. Nawet gdyby cena dobra spadła do zera, konsumenci nie chcieliby mieć go więcej.

Z tabeli wynika również, że gdy cena maleje, to całkowity przychód ze sprzedaży, obliczany jako iloczyn UC= Q*C najpierw rośnie, przy pewnym poziomie ceny i wielkości sprzedaży osiąga maksimum a potem maleje. Funkcja utargu całkowitego przyjmuje zatem postać paraboli skierowanej wierzchołkiem do góry

Zastanówmy się teraz, jakie są przyczyny takiego przebiegu funkcji utargu całkowitego oraz przy jakim poziomie ceny i sprzedawanych ilości utargu całkowity osiąga maksimum i zmienia się z rosnącego na malejący.

Jak wiemy utarg całkowity to suma utargów krańcowych UC=∑ΔUC/ΔQ, aby go obliczyć dla dowolnego poziomu sprzedaży, wystarczy je zsumować.

Nietrudno domyślić się, że utarg całkowity rośnie tylko wtedy, gdy utarg krańcowy jest większy od zera. Gdy utarg krańcowy jest równy zero utarg całkowity pozostaje bez zmian, natomiast, gdy jest ujemny, utarg całkowity maleje

W naszym przykładzie spadkowi ceny i wzrostowi kupowanych ilości towarzyszy malejący utarg krańcowy Uk Przy C=5 i Q=6 spada on do zera. W tym punkcie krzywej popytu utarg całkowity osiąga wielkość maksymalną UC=30. Natomiast przy cenach niższych utarg krańcowy przyjmują coraz większy wyrażeniu bezwzględnym wartości ujemne, zatem utarg całkowity maleje do zera.

Cena ( utarg przeciętny) a utarg krańcowy ( podejście analityczne)

Z tabeli powyżej wynika, że poza pierwsza sprzedaną jednostką przychód krańcowy z każdej kolejno sprzedanej jednostki Uk=ΔUC/ΔQ) jest zawsze mniejszy przychodu przeciętnego (Up =Q*C/Q=C), czyli ceny. Zobaczmy, skąd biorą się te różnice

Niech punktem wyjścia naszej analizy miedzy ceną i utargiem krańcowym będzie wyprowadzona z funkcji popytu funkcja utargu całkowitego:

UC = Q*C

Jak pamiętamy przyrost utargu całkowitego obliczamy według formuły:

ΔUC=Q*ΔC+ΔQ*C+ΔQ*ΔC

Jeżeli teraz ze względu na znikomą wartość pominiemy wyrażenie ΔQ*ΔC, wówczas otrzymujemy:

ΔUC= Q*ΔC+ΔQ* C

Aby obliczyć utarg krańcowy musimy obie strony równanie podzielić przez ΔQ

ΔUC C*ΔQ Q* ΔC

Uk = ------- = --------- + ---------

ΔQ ΔQ ΔQ

A po odpowiednich uproszczeniach otrzymujemy:

Q*ΔC

Uk= C + -----------

ΔQ

W realnym świcie cena C jest zawsze dodatnia, natomiast przy ujemnie nachylonej krzywej popytu wyrażenie:

ΔC

Q * -------

ΔQ

ma zawsze wartość ujemną. Wynika z tego, że obliczony według powyższego wzoru utarg krańcowy jest zawsze niższy od ceny rynkowej dokładnie o wartość tego wyrażenia

Ponieważ krzywa popytu przedstawia różne poziomy ceny (utarg przeciętny), dlatego też funkcja utargu krańcowego (pochodna od funkcji utargu całkowitego) przebiegać będzie pod funkcją popytu (linią ceny). Zauważmy dalej, że w miarę obniżania ceny i wzrostu sprzedaży rozpiętość pomiędzy ceną a utargiem krańcowy powiększa się.

Jeżeli funkcję popytu rynkowego przedstawia równanie C=a-b*Q wówczas funkcję przychodów całkowitych UC=C*Q ilustruje parabola o postaci UC= a*Q-b*Q
.

Pochodna od niej funkcja przychodu krańcowego ma postać Uk=a-2*b*Q. Jak widać nachylenie funkcji utargu krańcowego 2*b jest dwa razy większe od równego b nachylenia linii ceny, a to znaczy , ze jest ona dwa razy bardziej stroma

Gdy cena jest równa zero funkcja popytu przecina oś odciętych w punkcie a/b podczas gdy funkcja utargu krańcowego w punkcie a/2b, a to z kolei oznacza, że funkcja utargu krańcowy przecina oś odciętych Q w połowie odległości pomiędzy początkiem układu a punktem przecięcia się linii ceny z osią odciętych Rzutując ten punkt na krzywą popytu można zauważyć ze utarg krańcowy osiąga wartość równą zero dokładnie w połowie krzywej popytu. Jednocześnie w punkcie tym utarg całkowity osiąga maksimum. W wyjaśnieniu tego pomocna nam będzie pojecie elastyczności cenowej popytu. Związkiem między elastycznością a utargami całkowitymi i krańcowymi zajmiemy się w następnym punkcie przedtem jednak parę słów o narzędziach analizy trygonometrycznej

Rys Utarg krańcowy opada dwa raz szybciej niż cena

C, UC ,Uk

UC=max

UC= a*Q-b*Q

Cp

C=a-bQ

Uk= a-2*b*Q

0

(a/2*b) (a/b) Q

Utarg krańcowy i przeciętny a cena rynkowa. Analiza trygonometryczna

Dla naszej dalszej analizy szczególnie przydatna będzie kategoria utargu krańcowego oraz jej związek z utargiem przeciętnym Można to łatwo przedstawić trygonometrycznie.

W każdym punkcie krzywej utargu całkowitego jest równy wartości tangensa kąta nachylenia stycznej do tej funkcji, czyli tgα. Natomiast utarg przeciętny w dowolnym punkcie krzywej utargu całkowitego to wartość tangensa kąta nachylenia linii łączącej ten punkt z początkiem układu współrzędnych, czyli tg β

Rys. Trygonometryczny sposób przedstawia utargu krańcowego i przeciętnego

UC


UC

α

α

Q β Q

Uk UC

Uk

Q Q

0 0 Uk

Jeżeli każdej wartości utargu całkowitego przyporządkujemy odpowiednią wartość tgα, czyli utargu krańcowego, to otrzymamy funkcję utargu krańcowego - pochodną od funkcji utargu całkowitego. Ponieważ wraz ze spadkiem ceny kąt nachylenia stycznej maleje do zera, również do zera maleje utarg krańcowy. Jeżeli każdej wartości utargu całkowitego przyporządkujemy odpowiednią wartość tg β, to otrzymamy funkcję utargu przeciętnego. Ponieważ utarg przeciętny jest równy cenie, jest ona tożsama z funkcją popytu

Zauważmy, że dla każdego poziomu utargu całkowitego tgβ>tgα, a ponieważ utarg przeciętny równy jest cenie zatem dla każdego poziomu utargu całkowitego cena jest wyższa od utargu krańcowego. Wynika z tego, ze w przypadku niedoskonałej konkurencji utarg krańcowy jest mniejszy od ceny. Z geometrycznego punktu widzenia można powiedzieć, że krzywa marginalnych przychodów zawsze leży poniżej krzywej ceny - popytu).W dodatku wraz ze spadkiem ceny, odległość miedzy nimi powiększa się. Utarg krańcowy spada dwa razy szybciej niż cena

Elastyczność funkcji

Miary absolutne i względna

W analizach ekonomicznych często chcemy wiedzieć nie tylko o ile jednostek zmieniły się rozmiary popyty i cena, ale również jak silnie były te zmiany. Wymaga to odwołania się do wielkości stosunkowych. Dlaczego wielkości stosunkowe są tak ważne?

Po pierwsze możemy mieć do czynienia z różnymi nieporównywalnymi ze sobą ze sobą miarami ilościowymi np. kilogramy, metry, kilowatogodziny itp.

Po drugie przy tych samych miarach ilościowych nieporównywalne mogą być produkty np. kilogram jabłek i kartofli.

Po trzecie różny może być wyjściowy poziom analizowanych i zjawisk. Weźmy prosty przykład. Jakiś towar drożeje o 1 zł. Czy jest to duża podwyżka, czy mała? Na to pytanie możemy odpo­wiedzieć jedynie wtedy, gdy znamy jego wyjściową cenę. Jeżeli kosztująca 5 zł. puszka fasoli zdrożeje o 1zł, będzie to niewątpliwie bardzo duża podwyżka. Jeżeli z kolei cena samochodu wzrośnie o 1zł, będzie to dla kupujących podwyżka tak mała, że wręcz niezauważalna.

Elastyczność (elasticity, flexibility)

Z wymienionych wyżej powodów ekonomiści często odwołują się do obliczanych procentowa zmian względnych

Posługiwanie się wielkościami względnymi wręcz niezbędne, gdy chcemy porównywać ze sobą wyrażone w jednostkach fizycznych zmiany wielkości popyty czy podaży z wyrażonymi w jednostkach pieniężnych zmianami cen,

Porównania takie są potrzebne, gdy chcemy wiedzieć, nie tylko o ile zmieniają się rozmiary popytu czy podaży w wielkościach absolutnych, ale również z jaką intensywnością się one odbywają, inaczej mówiąc gdy chcemy ustalić siłę funkcjonalnych zależności, zachodzących między wielkościami ekonomicznymi.

Aby określić siłę reakcji popytu czy podaży na zmianę ceny czy dochodów ekonomiści wykorzystują zapożyczoną z matematyki kategorią elastyczności funkcji .Wrażliwość popytu na zmianę ceny nazywamy elastycznością cenową popytu, na zmianę dochodów elastycznością dochodową. Wrażliwość podaży na zmianę cen nazywamy elastycznością podaży.

Elastyczność cenowa popytu (ang. price flexibility of the demand),

Pojecie elastyczności popytu wprowadził do ekonomii w opublikowanej w 1890 r pracy p.t. „Zasady Ekonomii” Alfred Marshall (1842-1924) angielski filozof i ekonomista, wykładowca ekonomii na uniwersytecie w Bristolu, od 1883 profesor, a od 1885 kierownik katedry ekonomiki w King's College w Cambridge.

Szukając miary pokazującej, z jaką siłą zmienia się wielkość popytu na skutek zmiany ceny wyrobu lub usługi ,doszedł do wniosku ,że najlepiej mierzy to stosunek względnej zmiany wielkości popytu na dane dobro do względnej zmiany jego ceny, czyli tzw wskaźnik elastyczności cenowej popytu. Jego wartość oblicza się według następującej formuły

Ec= ΔQd/Qd :Δ C/C

gdzie:
Ec- wskaźnik elastyczności

Qd - dotychczasowy popyt na towar przy cenie C;

ΔQd - spadek lub wzrost popytu na skutek zmiany ceny;

C - dotychczasowa cena na towar x;

ΔC - wzrost (lub obniżenie) ceny na towar x.

znak "-" oznacza, że popyt zmienia się zazwyczaj (choć nie zawsze) w kierunku odwrotnym do zmiany ceny, (przyrost jednej z wielkości musi występować ze znakiem ujemnym).

Jak pokażemy dalej można mówić o elastyczności całej krzywej popytu, zanim jednak do tego dojdziemy zastanówmy się nad problemami związanymi z pomiarem elastyczności popytu na łuku , czyli między dwoma dowolnymi punktami leżącymi na krzywej popytu.

Elastyczność na łuku i w punkcie

Elastyczność cenową popytu zdefiniowaliśmy jako stosunek procentowej, czyli względnej, zmiany wielkości zapotrzebowania do procentowej, czyli względnej, zmiany ceny.

Ec = -ΔQd/Qd: Δ C/C

Rys. Tabela i wykres funkcji popytu

C Δ C Qd ΔQ

C

10 A A 10 - 0 -

8 B B 8 -2 10 +10

6 C C 6 -2 20 +10

4 D D 4 -2 30 +10

2 E E 2 -2 40 +10

0 F 0 -2 50 +10

10 20 30 40 50 Q

Weźmy dla przykładu funkcję popytu, zapisaną w powyżej tabeli i wykreśloną na rysunku. Jak obliczyć wartość wskaźnika elastyczność popytu między punktami B i C? Musimy w tym celu określić wartości liczbowe ΔQ i Q oraz ΔC i C. Już na początku mamy problem, jak należy mierzyć procentowe zmiany obu wielkości? Z przyrostami nie mamy kłopotu, bo w przypadku funkcji liniowej są to wielkości stałe. Powstaje natomiast problem, jakie wartości należy przypisać zmiennym C i Q? Czy też za podstawę obliczeń przyjmować wartość tych zmiennych w punkcie A, czyli gdy cena maleje, czy może w punkcie B, gdy cena rośnie? Dlaczego problem? Bo za każdym razem dostajemy inny wynik, a zatem mamy do czynienia z niejednoznacznością .

Absolutne i względne zmiany ilości

Różnica ilości żądanej przez nabywców(ΔQ) między punktami B (10) i C (20) wynosi w wartościach absolutnych 10:

ΔQ= 20 -10 = 10.

Nie jest natomiast jasne ile wynosi zmiana względna, (ΔQ/Q). Będzie ona różna w zależności od tego to, jaka wielkość przyjmiemy za podstawę porównań. Jeżeli weźmiemy popyt w punkcie B(Q=10), to zmiana względna ΔQ/Q wynie­sie 10/10.W przypadku punktu C (Q=20), wyniesie ona 10/20. Różnica będzie tym większe, im bardziej oba punkty B i C są od siebie oddalone. Mamy, zatem do czynienia z pewną mniejszą lub większa dwuznacznością, którą należałoby jakoś usunąć lub ją przynajmniej zminimalizować. Będzie to możliwe, jeśli za podstawę obliczeń weźmiemy średnią arytmetyczną z ilości zanotowanych w obu punktach: wyjściowym i do­celowym:

20+10

Qd =- ---------= 15

2

Uśrednione w ten sposób tempo zmian popytu wynosi ΔQ/Q= 10/15

Absolutne i względne zmiany cen

Podobna sytuacja występuje w przypadku cen. Różnica między ceną w punkcie B (8) i punkcie C (6) wynosi, -2 zatem ΔC=-2. Względną zmianę ceny obliczamy podobnie jak względną zmianę ilości. Za podstawę przyjmujemy cenę średnią

8+6 14

C= ----------= --------= 7

2 2

Uśrednione tempo zmiany cen wynosi ΔC/C=2/7.

Elastyczność lukowa

Po obliczeniu uśrednionych temp zmian popytu i ceny możemy wyznaczyć wartość liczbową wskaźnika elastyczności. Zgodnie z przedstawionym tutaj sposobem, zwanym metodą „punktu środkowego", elastyczność cenową popytu obliczamy według formuły:

ΔQ ΔC

Ec= -----------: -----------

średnia Q średnia C

W naszym przykładzie średnia wartość wskaźnika elastyczność popytu między punktami A i B, czyli na łuku wynosi: (10/15): (-2/7)= -7/3 =-2,33.

Elastyczność w punkcie

Gdyby przyrosty obu ilości i ceny były nieskończenie małe, lub mówiąc językiem matematycznym gdyby dążyły do zera, co zapisujemy jako (Q1- Q0) -->0 oraz (C1- C0) -->0, to w tym szczególnym przypadku, oba punkty B i C, jak to pokazano na zamieszczonym poniżej rysunku, zbliżyłyby się do siebie na tak małą (nieskończenie) odległość, że zlałyby się w jeden. Ponieważ w tej sytuacji różnica podstaw jest również nieskończenie mała, zatem wskaźnik elastyczności da identyczne wyniki bez względu na to czy liczymy go w dół czy w górę funkcji.

Rys Elastyczność w punkcie na funkcji ciągłej

Cena

B<=>C

Qd

Przy nieskończenie małych różnicach ilości i cen z matematycznego punktu widzenia mamy do czynienia z funkcją ciągłą. Aby obliczyć wartość wskaźnika elastyczności musimy odwołać się do matematycznej formuły elastyczności funkcji, która zapisujemy jak poniżej:

Ec=

Gdzie :Y to jest odpowiednikiem popytu Qd, zaś X to odpowiednik ceny rynkowej

Obliczony w ten sposób wskaźnik elastyczności odzwierciedla siłę związku procentowych zmian ilości i cen przy nieskończenie małych ich zmianach, czyli w danym punkcie (cena - ilość) na krzywej popytu, dlatego ten sposób liczenia elastyczności nazywamy elastycznością liczoną w punkcie a uzyskany wynik to wskaźnik elastyczności punktowej.

Zmiany nieskończenie małe występują tylko w matematyce, nie ma ich natomiast na rynku. Tam ceny i rozmiary popytu zmieniają się skokowe o konkretne wymierne wielkości inaczej mówiąc są to zmienne dyskretne. W analizach realnych wielkości rynkowych nie możemy, zatem posługiwać się pojęciem punktu na funkcji popytu, tylko musimy wziąć pod uwagę fakt, że znajdujemy na łuku.

W praktyce punktowy sposób pomiaru elastyczności może być stosowany, ale tylko przy niewielkich zmianach ceny (np. rzędu 1%). Byłby jednak błędny przy dużych zmianach cen, gdyż w zależności od tego czy cena spada, co ilustruje przejście z punktu B do punktu C, czy rośnie, z kolei ilustruje przejście z punktu C do punktu B uzyskiwalibyśmy dwa istotnie różne wyniki. I tak gdy B->C Ec= 10/10:-2/8=- 4, natomiast gdy C->B Ec=-10/20:2/6=-1,5

Przy dużych zmianach cen, należy, zatem liczyć elastyczność łukową jako wielkość średnią między dwoma punktami na krzywej.

Znak

Krzywe popytu są na ogół nachylone w dół. Oznacza to, że poza nielicznymi wyjątkami wielkość zapo­trzebowania zmienia się w przeciwnym kierunku niż cena. Wyjątek stanowią, np. niektóre relatywnie tanie dobra podstawowe, zwłaszcza najtańsze rodzaje żywności (ziemniaki itp.), na które popyt może wzrastać, pomimo (i na skutek) wzrostu ich ceny. Dzieje się tak dlatego, że uszczuplenie w rezultacie wzrostu cen realnych dochody uboższych warstw ludności powo­dują zmniejszenie spożycia lepszych gatunków żywności, ubytek ten kompensowany jest zwiększoną konsumpcją niższych gatunków żywności które, pomimo że zdrożały, pozostają w dalszym ciągu dużo tańsze. Dodatni znak wskaźnika elastyczności cenowej popytu jest skutkiem tzw. paradoks Giffena.

Z reguły jednak wzrost ceny (zmiana dodatnia) powoduje spadek zapotrzebowania (zmiana ujemna). Podobnie spadek ceny (zmiana ujemna) powoduje wzrost zapotrzebowania. Tak, więc przy obliczaniu wskaźnika elastyczności cenowej popytu poza sytuacjami szczególnymi dzielimy wielkość ujemną przez wielkość dodatnią lub na odwrót - wielkość dodatnią przez ujemną. W obu przypadkach otrzymuje­my najczęściej liczbę ujemną.

Wartość liczbowa wskaźnika

Miarą elastyczności cenowej jest stosunek względnego wzrostu popytu do względnego wzrostu ceny. Jeżeli pominiemy ujemny znak elastyczności cenowej popytu i skupimy uwagę na wartości bezwzględnej |Ec| to informuje ona, czy i na ile popyt jest elastyczny. Wyróżniamy następujące wartości graniczne oraz przedziały wartości:

Popyt elastyczny| Ec |>1

Popyt jest elastyczny, gdy dana zmiana procentowa ceny wywołuje większą od niej procentową zmianę wielkości zapotrzebowania. Zapisujemy to w postaci nierówności ΔQ/Q>ΔC/C

W tym przypadku wartość wskaźnika elastycz­ność |Ec|= ΔQ/Q:ΔC/C>1, ponieważ licznik ułamka jest większy od mianownika. Im wyższa bezwzględna wartość wskaźnika, tym w badanym przedziale cenowym popyt jest bardziej elastyczny.

Popyt nieelastyczny |Ec| < 1

Popyt jest nieelastyczny, gdy dana procentowa zmiana ceny powoduje mniejszą procentowo zmianę wielkości zapotrzebowania, czyli gdy ma miejsce nierówność ΔQ/Q>ΔC/C

W tym przypadku |Ec| =ΔQ/Q:ΔC/C przyjmuje w badanym przedziale cenowym bezwzględną wartość mniejszą od jedności. Im jest ona niższa, tym popyt jest mniej elastyczny.

Popyt o elastyczności jednostkowej | Ec| = 1

Popyt ma elastyczność równą 1, gdy zmianie ceny towarzyszy taka sama procentowo zmiana wielkości zapotrzebowania. W tych warunkach Q/Q=ΔC/C zatem wskaźnik elastyczności| Ec| =ΔQ/Q:ΔC/C przyjmuje wartość 1, ponieważ licznik ułamka jest równy mianownikowi.

Popyt sztywny Ec = 0

Popyt jest sztywny, gdy wartość wskaźnika |Ec| =ΔQ/Q:ΔC/C= 0. Ma to miejsce wtedy, gdy dodatnim lub ujemnym zmianom cen ΔC nie towarzyszą żadne zmiany zapotrzebowania na dany produkt ΔQ=0.

Popyt doskonale (nieskończenie) elastyczny Ec = -oo

Występuje wtedy, kupowane ilości rosną lub maleją ΔQ różne od 0 nawet, gdy poziom cen pozostaje, niezmienionym ΔC=0. Ponieważ mianownik ułamka Ec==ΔQ/Q:ΔC/C przyjmuje wartość zero, zatem cały ułamek przyjmuje wartość nieskończenie dużą.

Elastyczności na krzywej a elastyczność krzywej

Częstym błędem w interpretacji elastyczności cenowej popytu jest mniemanie, że można mówić o danej i stałej elastyczności w odniesieniu do całej krzywej popytu. Bierze się on najczęściej stąd, że utożsamia się elastyczność z nachyleniem krzywej popytu. Błąd polega na tym, że w większości przypadków wartość mierzącego elastyczność wskaźnika zmienia się wzdłuż danej krzywej popytu, natomiast nachylenie funkcji popytu, (jeśli jest to linia prosta), pozostaje niezmienione.

Analiza algebraiczna

Z zależności czysto algebraicznych wynika, że na ujemnie nachylonej liniowej krzywej popytu spadkowi ceny towarzyszą coraz mniejsze wartości wskaźnika w wyrażeniu bezwzględnym. Im wyższa cena, tym większa jest jego bezwzględna wartość wskaźnika, tym popyt jest bardziej elastyczny, natomiast ·w miarę spadku ceny elastyczność popytu maleje. W uzasadnieniu tego zjawiska odwołamy się do prostej matematyki.

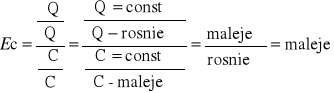
Załóżmy, że przesuwamy się w dół po lini9owej krzywej popytu, z zachowaniem jednakowych każdorazowych stałych zmian ceny ΔC=const i popytu ΔQ=const .

Jednak w miarę obniżania się ceny zmienią się podstawy służące do obliczania procentowych zmian ilości i cen. Ilości Q stają się coraz większe natomiast ceny C coraz mniejsze. W tych warunkach licznik ułamka maleje , mianownik rośnie, w rezultacie spadać musi jego bezwzględna wartość. Inny sposób na wyjaśnienie tego zachowania dostarcza nam analiza trygonometrycznej.

Analiza trygonometryczna zachowanie wskaźnika elastyczności

Aby przedstawić geometryczny obraz elastyczności i ułatwić jej analizę na danej funkcji popytu przekształćmy formułę elastyczności do postaci jak poniżej:

ΔQ C

Ec=- ------* ------

ΔC Q

Wyraz ΔQ/ΔC, to odwrotność nachylenie funkcji popytu w danym punkcie (tj. przy rozpatrywanym wyjściowym poziomie ceny), zaś wyraz C/Q - pokazuje stosunek ceny do ilości dobra kupowanej przy tej cenie.

A teraz poszukajmy tych wielkości na znanej nam liniowej krzywej popytu którą charakteryzuje stałe nachylenie mierzona stosunkiem ΔC/ΔQ,

Rys Trygonometryczna interpretacja elastyczności cenowej popytu

C Cp A Ec= -oo

| Ec |> |-1|

α Α B | Ec|= -1

*

α B Ec| <| -1|

C

β) β ) ( α C Ec=0

0 Qd 0 Qd

Na powyższym rysunku trygonometryczną miarą wyrażenia ΔQ/ΔC jest ctgα=1/tgα, zaś miarą C/Q jest tgβ. Wykorzystując funkcje trygonometryczne wskaźnik elastyczności możemy zapisać w nieco odmienny sposób jak poniżej:

tg β

Ec= - ctg α* tg β = ------------

- tg α

Naszą analizę prowadzimy w warunkach spadku ceny W przypadku, gdy funkcja popytu jest linią prostą, jej nachylenie jest stałe. Inaczej mówiąc kąt α a co za tym ctgα i tg są w każdym punkcie funkcji stałe. Stały jest zatem mianownik ułamka. Natomiast w miarę przesuwania się na prawo w dół kąt β a co za tym wartość tg β maleje. Wynika z tego, że wskaźnik elastyczności cenowej Ec=tgβ/-tgα przyjmuje w punkcie A na rysunku z lewej strony większą wartość niż w punkcie B. Znaczy to, że popyt na dane dobro jest bardziej elastyczny przy wyższej cenie a mniej elastyczny przy cenie niższej. Im niższe ceny tym niższa jest bezwzględna wartość tego wskaźnika.

Z rysunku po prawej stronie wynika, że w punkcie A przy cenie prohibicyjne Cp, przy której popyt jest równy zero tgβ=∞, wartość wskaźnika elastyczności wynosi Ec=∞/-tgα=-∞. Dokładnie w połowie funkcji popytu β=α a to oznacza że w punkcie B wskaźnik ten osiąga wartość Ec=-1. Przy cenach niższych |Ec |< 1 W punkcie C przy cenie równej zero tgβ=0, zatem wartość wskaźnika elastyczności cenowej popytu wynosi w tym punkcie Ec=0.

Elastyczność na linii wypukłej względem początku układu

W przypadku, gdy funkcja popytu nie jest linią prostą tylko np. jak to pokazano na rysunku poniżej wypukła względem początku układu współrzędnych, wówczas miarę obniżki ceny, czyli poruszania się po krzywej na prawo w dół jej kąt nachylenie a co za tym wartość tgα w wyrażeniu bezwzględnym maleje natomiast bezwzględna wartość ctgα rośnie. Z drugiej strony w miarę obniżki ceny maleje, kąt β a wraz nim maleje tg β

Rys. Elastyczność na linii wypukłej

C tg β

α Ec=-------------

A tgα

B

α`

Q

β β`

W tej sytuacji nie można określić ogólnie i jednoznacznie, jakie wartości przyjmuje wskaźnik elastyczności cenowej Ec. Wartość wskaźnika zależy od wypukłości krzywej. Dla krzywej o niewielkiej wypukłości, czyli kształcie zbliżonym do prostej, możemy z dużym prawdopodobieństwem przyjąć, że Ec maleje wraz ze spadkiem ceny.

Elastyczność krzywej popytu

Mówiąc o jakiejś konkretnej wartości wskaźnika elastyczności wskazującej czy popyt jest elastyczny czy nie mamy w zasadzie na myśli jedynie pewien wycinek krzywej popytu. Od zasady tej istnieją jednak dwa wyjątki. Pierwszy dotyczy szczególnych postaci krzywych popytu, które mają jednakową elastyczność na całej długości.

Drugi wyjątek dotyczy sytuacji, kiedy porównujemy dwie krzywe popytu wykreślone w tym samym układzie współrzędnych. W tym przypadku, kierując się tylko wartością nachylenia krzywych, możemy stwierdzić, że krzywe o większym nachylenie bardziej strome są przy każdej cenie mniej elastyczna niż krzywe o mniejszym nachyleniu, czyli bardziej płaskie. Zacznijmy od tego przypadku.

Elastyczność a nachylenie krzywej popytu

Często interesuje nas ogólna ocena elastyczności na całej długości krzywej popytu, tzn. przy różnych poziomach ceny. Na przykład, popyt na dobra luksusowe jest zwykle bardziej elastyczny niż popyt na dobra podstawowe - i to przy każdym poziomie ceny.

Załóżmy, że mamy dwie krzywe o rożnym nachyleniu D1 i D2, które przecinają się w punkcie A, przy cenie C0, i ilości Qd0. Zobaczmy, jaka jest elastyczność popytu na obu rynkach w sytuacji, gdy cena spada do poziomu C1.

Przy wspólnej podstawie ilościowej i takiej samej zmianie poziomu ceny wartość cenowej elastyczności popytu, zależeć będzie od zmian rozmiarów popytu, a te zależą od nachylenia funkcji.

Rys Elastyczność a nachylenia krzywej

C D1

ΔC=const

D2 (Qd1-Qd0) >(Qd1 -Qd0)

A

C0

C1 B C

Qd0 Qd1 Qd2 Qd

W przypadku funkcji D1 o większym nachyleniu, bardziej stromej znajdziemy się w punkcie B. Danemu wzrostowi ceny o ΔC=C1-C0 towarzyszyć będzie wzrost wielkości popytu do poziomu, Qd1, czyli popyt przyrośnie ΔQd= Qd1 -Qd0.

Na krzywej popytu D2 ten sam spadek wywoła dużo większy wzrost kupowanych ilości ΔQd= Qd2-Qd0. W tym przypadku ten sam procentowy wzrost ceny spowoduje większy procentowo wzrost popytu. Możemy zatem powiedzieć, że dla dowolnego punktu na krzywej wskaźniki cenowej elastyczności popytu są wyższe dla krzywej o mniejszym nachyleniu i niższe dla krzywej o większym nachyleniu.

Z rysunku powyższego wynika, że z dwóch krzywych popytu umieszczonych w tym samym układzie współrzędnych bardziej elastyczna jest krzywa o mniejszym nachyleniu (płaska) a mniej elastyczna jest bardziej stroma.

Jednocześnie należy pamiętać, że każda z nich będzie miała różną elastyczność w różnych punktach, chyba że są to przypadki szczególne krzywych o stałych elastycznościach.

W analizie elastyczności popytu możemy kierować się następującą wskazówką: popyt o wysokiej elas­tyczności wyraża krzywa o małym nachyleniu (płaska); popyt nieelastyczny wyraża krzywa o dużym nachyleniu (stroma).

Przypadki szczególne. Funkcje o stałej elastyczności

W analizach rynku będziemy mieli do czynienia z nietypowymi funkcjami o stałej elastyczności są przypadki szczególne: Dalszej analizie poddamy analizie trzy takie przypadki popytu:

1. popyt na całej długości funkcji jest doskonale nieelastyczny (Ec=0);

2. popyt na całej długości funkcji nieskończenie elastyczny (Ec=-oo);

3. popyt na całej długości ma stałą elastyczność jednostkowej elastyczności (Ec=-1)

Popyt zupełnie nieelastyczny (sztywny).

Niekiedy krzywa popytu przyjmuje postać linii prostej pionowej. Bez względu na wysokość ceny nabywcy kupują taką samą ilość. Ponieważ ΔQ.= 0, zaś ΔC jest różne od zera , zatem współczynnik elastyczności na całej długości funkcji przyjmuje wartość Ec=0.

Rys Popyt doskonale nieelastyczny (sztywny)

C D

C1

C0

Qd= const Qd

Popyt nieskończenie( doskonale) elastyczny.

Krzywa popytu ma postać linii prostej poziomej. Na rysunku poniżej przy każdej cenie wyższej od C0 popyt wynosi zero. Natomiast przy cenie C (lub niższej) popyt jest „nieskończenie" wielki. Ponieważ wartość ΔC=0, zaś ΔQ jest różne od zera, zatem współczynnik elastyczności przyjmuje na całej długości funkcji wartość Ec= - ∞.

Taki kształt krzywej popytu, pozornie mało prawdopodobny, jest przynajmniej w teorii, odzwierciedla popyt na wyroby pojedynczego producenta na rynku doskonale konkurencyjnym. Jak już wyjaśnialiśmy w warunkach konkurencji doskonałej podaż pojedynczego przedsiębiorstwa jest niezmiernie mała w stosunku do podaży rynkowej (w takiej sytuacji jest, np. drobne gospodarstwo rolne jako producent zboża).

Rys Popyt doskonale elastyczny

C

C0 D

Qd0 Qd1 Qd

Takie przedsię­biorstwa muszą zaakceptować cenę określoną przez stosunek podaży i popytu na całym rynku, ale po tej cenie mogą sprzedać każdą ilość zboża, którą wyprodukują (całkowity popyt rynkowy na zboże ma swoje granice, ale popyt na zboże dostarczane przez danego rolnika po cenie równowagi rynkowej jest praktycznie nieograniczony). W tym przy­padku im więcej zboża rolnik wytworzy i sprzeda, tym większy będzie miał przychód. Na rysunku powyżej w punkcie Qd1 utarg jest większy aniżeli w punkcie Qd0.

Funkcja o stałej jednostkowej elastyczności popytu

Jak pamiętamy elastyczność cenowa ujemnie nachylonej liniowej funkcji popytu jest zmienna? Spada wraz ze spadkiem ceny, a w samym środku funkcji przyjmuje wartość równą jedności. Może się jednak zdarzyć, że współczynnik elastyczności wynosi E c=-1 na całej długości funkcji. Oznacza to, że niezależnie od wyjściowego poziomu ilości i ceny, dowolnym procentowym zmianom ceny odpowiada zawsze tak sama procentowa zmiana popytu.

Może sądzicie, że krzywa popytu o jednostkowej elastyczności będzie linią prostą o nachyleniu 45°, tymczasem przedstawienie takiej zależności będzie możliwe, gdy odejdziemy od założenia o liniowym charakterze funkcji popytu i zastąpimy ją pokazaną poniżej funkcją zwaną hiperbolę równoramienną. Osiągnięcie równości temp wymaga, by absolutne przyrosty popytu były odpowiednio coraz większe, natomiast absolutne spadki cen coraz mniejsze. Oznacza to, że musi mieć ona zmienne nachylenia na całej długości i to takie, by przyrosty obu wielkości w stosunku do podstaw dawały w każdym punkcie krzywej te same tempa wzrostu oby wielkości.

Rys .Hiperbola równoramienna

C ΔC ΔC/C Q ΔQ ΔQ/Q Ec

C A 50 - - 100 - -

A B 40 10 0, 2(2) 125 25 0,(2) 1, 0

C 30 10 0, 28 166 41 0,28 1, 0

B Ec=1 D 20 10 0, 4 250 84 0,4 1, 0

E 10 10 0, 6(6) 500 250 0,6(6) 1 0

C

D

E Qd

Na przykład, wzrost ilości z 100 do 125 jest w ujęciu względnym taki sam jak wzrost ze, 125 do 200, choć przyrost bezwzględny jest dwa razy większy. Podobnie spadek ceny z 5 do 2,5 zł 5 jest procentowo taki sam jak spadek z 10 do 5 zł, ale w wymiarze absolutnym jest on dwa razy mniejszy.

Elastyczność popytu a utarg krańcowy i całkowity

Dokładniejsze zależność między zmianą poziomu ceny wysokością współczynnika elastyczności popytu a wysokością utargu całkowitego przedstawić można syntetycznie w postaci tabeli, jak poniżej

Punkt	Cena	ΔC	ΔC/C	Q(tys)	ΔQ	ΔQ/Q	Ec	UC=Q*C	Uk= ΔUC/ΔQ
A	110	-	-	0	-	-		0	-
B	100	-10	0,095	10	10	1.0	10,52	100 000	1000
C	90	-10	0,105	20	10	0,6(6)	6,28	180 000	800
D	80	-10	0,117	30	10	0,4	3.4	240 000	600
E	70	-10	0,13(3)	40	10	0,28	2,1	280 000	400
F	60	-10	0,153	50	10	0,2(2)	1,4	300 000	200
G	50	-10	0,18	60	10	0,18	1,0	300 000	0
H	40	-10	0,2(2)	70	10	0,153	0,68	280 000	-200
I	30	-10	0,28	80	10	0,13(3)	0,46	240 000	-400
J	20	-10	0,4	90	10	0,117	0,29	180 000	-600
K	10	-10	0,6(6)	100	10	0,105	0,15	100 000	-800
L	0	-10	1,0	110	10	0,095	0,095	0	-1000

Dane zawarte w tabeli można przedstawić, w postaci dwuwymiarowych wykresów funkcji popytu, utargu całkowitego i krańcowego Na osi odciętych odkładamy tradycyjnie kupowane ilości Q natomiast na osi rzędnych oprócz ceny odkładamy dodatkowo wartości utargu całkowitego oraz utarg krańcowego towarzyszące różnym sprzedawanym ilościom.

Rys Elastyczność popytu a utarg całkowity i krańcowy

C ,UC

UC=300 000

Ec>1

Ec=1

C=50

Ec<1

Qd

Qd=60

Przychód całkowity przeciętny i krańcowy a cena rynkowa i wielkość sprzedaży

Z przedstawionych w tabeli danych i ilustrującego je wykresu wynika, że przy liniowej (funkcji popytu, spadkowi ceny na górnej połówce funkcji gdzie popyt jest elastyczny towarzyszy wzrost, a wzrostowi spadek utargu całkowitego. W połowie funkcji gdzie elastycznością cenowa wynosi Ec=-1, W punkcie tym zmiany cen i ilości nie wywołuje żadnych zmian w utargu całkowitym Na tym odcinku funkcji popytu utarg osiąga maksimum. Natomiast na dolnej połówce gdzie popyt jest nieelastyczny, spadkowi ceny towarzyszy spadek zaś wzrostowi cen wzrost utargu całkowitego

Wynika z tego, że spowodowany zmianami cen kierunek zmian utargu całkowitego zależy od wartością elastyczności cenowej popytu. Gdy popyt jest elastyczny utarg zmienia się w kierunku odwrotnym do zmiany ceny. To znaczy, gdy cena maleje utarg krańcowy jest dodatni a gdy rośnie ujemny. Z kolei gdy popyt jest nieelastyczny zmiany idą w tym samym, kierunku to znaczy, że utarg krańcowy jest dodatni, gdy cena rośnie i ujemny, gdy maleje. Gdy elastyczność jest równa jedności, zmiany cen nie powodują zmian utargu, to znaczy, że utarg krańcowy jest równy zero.. Spróbujemy teraz wyjaśnić skąd biorą się te zależności

Elastyczność a utarg krańcowy

Ilościowym wyrazem wpływu zmian cen i ilości na poziom utarg całkowitego jest jego przyrost ΔUC. Gdy przyjmuje wartość dodatnią ΔUC >0 , utarg całkowity rośnie, gdy ujemną ΔUC<0,utarg całkowity maleje gdy zerową ΔUC=0, utarg całkowity pozostaje niezmieniony. Jak pamiętamy wzór na przyrost utargu całkowitego możemy z pewnym uproszczenie zapisać jak poniżej:

ΔUC= | ΔQ*C | + | ΔC*Q |

Z przedstawionego wzoru wynika, że na wielkość i kierunek przyrostu utargu całkowitego wpływają dwa działające w przeciwnych kierunkach efekty. Wyrażenie ΔQ*C rejestruje wpływ czynnika ilościowego. Gdy ilości rosną ma ono wartość dodatnią, gdy maleją ujemną. Oznacza to, że wzrost ilości towarzyszy dodatni, a spadkowi ujemny cząstkowy przyrost utargu całkowitego. Z kolei wyrażenie ΔC*Q rejestruje wpływ czynnika cenowego. Gdy cena rośnie, ma ono wartość dodatnią, gdy cena maleje ujemną. Oznacza to, że wzrostowi ceny towarzyszy dodatni, a spadkowi ujemny cząstkowy przyrost utargu całkowitego.

Zgodnie z prawem popytu oba efekty działają w przeciwnych kierunkach, ale niekoniecznie z równa siłą. Jeżeli spadkowi lub wzrostowi ceny towarzyszy nierówność:

| ΔQ*C| >| ΔC* Q|

to znaczy, że ilościowy efekt zmiany utargu całkowitego działa silniej niż cenowy. W tych warunkach utarg całkowity zmienia się w kierunku przeciwnym do zmiany ceny. Spadkowi ceny towarzyszy wzrost utargu całkowitego, natomiast wzrostowi ceny towarzyszy spadek utargu całkowitego. Wynika z tego, że przy tego typu nierówność, popyt jest elastyczny Aby to uzasadnić podzielmy obie jej strony przez utarg całkowity

UC= Q*C

| ΔQ*C | | ΔC*Q |

----------- > -------------

Q*C Q*C

Po stosownych uproszczeniach otrzymujemy

| ΔQ | | ΔC |

----------- > -----------

Q C

Z nierówności tej wynika, że efekt ilościowy działa silniej, gdy tempo zmian kupowanych ilości jest większe od tempa zmian cen.

Podzielmy teraz nierówność stronami przez |ΔC|:C. W rezultacie otrzymujemy nierówność:

| ΔQ | | ΔC |

Ec = --------- : --------- >1

Q C

Jej lewa strona nierówności to stosunek tempa wzrostu popytu do tempa wzrosty cen, czyli znany nam miernik elastyczności cenowej popytu. Gdy jego wartość jest większa od jedności, popyt jest elastyczny. W ten sposób dowiedliśmy, że gdy popyt jest elastyczny utarg całkowity zmienia się w kierunku przeciwnym do zmiany ceny. Gdy cena maleją utarg całkowity rośnie zatem utarg krańcowy jest większy od zera ,z kolei gdy cena rośnie utarg całkowity maleje zatem utarg krańcowy jest ujemny.

Z kolei efekt cenowy działa silniej niż ilościowy, gdy zmianom ceny towarzyszy nierówność:

| ΔQ * C | < | ΔC * Q |

po analogicznych przekształceniach dochodzimy do nierówności:

| ΔQ * | | ΔC |

Ec = ----------- : --------- <1

Q C

Wynika z niej, że gdy popyt jest nieelastyczny spadkowi ceny towarzyszy ujemny utarg krańcowy i spadek utargu całkowitego, natomiast wzrost ceny przynosi dodatni utarg krańcowy , a co za tym utarg całkowity rośnie

Gdy oba efekty działają z jednakową siłą:

| ΔQ*C | = | ΔC*Q |

przyrost utargu całkowitego wyniesie zero. W tej sytuacji pomimo zmiany ceny i ilości utarg całkowity pozostanie bez zmian. Stosując poznane procedury dochodzimy do równości

| ΔQ | | ΔC |

Ec=----------- : --------- = 1

Q C

Wynika z niej że zmiany cen i ilości nie wpływają na wielkość utargu całkowitego (utarg krańcowy jest równy zero), gdy popyt wykazuje elastyczność jednostkową

Z przedstawionej powyżej analizy wynika, że na górnej połówce liniowej funkcji popytu gdzie utarg krańcowy jest dodatni Ec>|-1 |. W połowie funkcji gdzie utarg krańcowy jest równy zero Ec|=|-1|. Na dolnej połówce funkcji gdzie utarg krańcowy jest ujemny Ec < |-1|

Wiemy również, że dla funkcji w postaci linii prostej wraz ze spadkiem ceny i wzrostem sprzedaży elastyczności w wartościach bezwzględnych |Ec| spadają od nieskończoności do zera. Wartość Ec=|- 1| osiągają w połowie funkcji popytu.

Utarg krańcowy a elastyczność cenowa popytu (ujęcie analityczne)

Powróćmy do równania opisującego przychód krańcowy

ΔC

Uk= C + Q * -------

ΔQ

Jeżeli teraz wyciągniemy przed nawias cenę C to otrzymamy:

1 Q * ΔC

Uk= C {1 + --------- * ----------- }

C ΔQ

Po niewielkim przekształceniu dochodzimy do postaci :

Q ΔC

Uk= C { 1 + ------- * --------- }

C ΔQ

Wartość wskaźnika elastyczności cenowej popytu

ΔQ/Q

Ec= -----------

ΔC/C

możemy przekształcić do postaci

ΔQ C

Ec=- ------* ------

ΔC Q

Zatem iloczyn zawarty w nawiasie równania opisującego utarg krańcowego może być wyrażony jako odwrotnością elastyczności cenowej popytu

Q ΔC 1

--------- * --------- = ------

C ΔQ Ec

Oznacza to, że formułę utargu krańcowego możemy przedstawić w bardziej użytecznej dla analizy interesujących nas zależności postaci:

1

Uk = C (1 + ---- )

Ec

Uk = C+ C*1/ Ec

Ponieważ w miarę spadku ceny elastyczność cenowa popytu spada w wielkościach absolutnych, rośnie zatem w wielkościach absolutnych wartość wyrażenie 1/Ec a tym samym rośnie wartość wyrażenia C*1/ Ec, które po odjęciu od ceny daje wartość utargu krańcowego Wynika z tego, że w miarę spadku ceny utarg krańcowy maleje i na odwrót gdy cena rośnie, to wartość wyrażenie 1/Ec. w wielkościach absolutnych maleje, a to oznacza , że utarg krańcowy rośnie

Jeśli popyt jest nieelastyczny Ec < |- 1| to wyrażenie 1/Ec jest większe od jedności, a ponieważ ma ono wartość ujemną, zatem wyrażenie (1-1/Ec ) będzie miało również wartość ujemna , a zatem gdy popyt jest nieelastyczny , przychód krańcowy jest ujemny .

Jeśli natomiast elastyczność cenowa popytu jest większa od jedności Ec>|-1|, to przeprowadzając podobne rozumowania to wyrażenie 1/Ec< |-1| jest mniejsze od jedności, a ponieważ ma ono wartość ujemną zatem wyrażenie (1-1/Ec ) będzie miało wartość dodatnią a zatem przychód krańcowy jest dodatni.

Z przedstawionej wyżej formuły utargu krańcowego wynika, że jeżeli elastyczność cenowa popytu wynosi Ec=-1, to przychód krańcowy wynosi Uk =C(1-1/1)=0 W tych warunkach zmiana poziomu cen nie powoduje zmiany utargu całkowitego

Jeżeli popyt jest doskonale elastyczny, to wyrażenie1/Ec jest równe zero, zatem utarg krańcowy Uk = C+ C*1/ Ec jest równy cenie

Z kolei, jeśli elastyczność cenowa wynosi Ec=0, czyli gdy popyt jest sztywny, to wyrażenie 1/Ec jest nieskończenie duże, zatem utarg krańcowy Uk = C+ C*1/ Ec przyjmuje nieskończenie duże wartości ujemne

Utarg krańcowy i elastyczność cenowa na liniowej krzywej popyt- ujęcie geometryczne

Wróćmy teraz do wykresów interesujących nas funkcji Jak wynika z powyższych rozważań, wzrost lub spadek utargu całkowitego uzależniony jest od wartości utargu krańcowego, a ten z kolei zależy od wartości współczynnika elastyczności cenowej popytu Ec.

Na górnym odcinku liniowej krzywej popytu, gdzie elastyczność cenowa popytu jest większa od jedności utarg krańcowy jest większy od zera, zaś utarg całkowity rośnie wraz ze spadkiem ceny i spada, gdy cena rośnie. W połowie funkcji popytu gdzie elastyczność jest równa jedności i, utarg krańcowy jest równy zero, zaś utarg całkowity pozostaje bez zmian pomimo zmian ceny i ilości. Wreszcie na dolnej połowie funkcji popytu, gdzie elastyczność cenowa jest mniejsza od jedności utarg krańcowy jest mniejszy od zera, co oznacza, że utarg całkowity spada, gdy cena spada oraz rośnie wraz z jej wzrostem.

Rys Elastyczność a utarg krańcowy i całkowity

C

Uk D

Up

Ec > 1 Uk>o

C* Ec = 1 Uk=0

Ec <1 Uk<0

D

Q* Q

UC Uk

UC=max

Q

Q*

Elastyczność funkcji nachylonych dodatnio

Zmiana ceny powoduje nie tylko zmianę wielkości popytu, lecz także zmianę wielkości podaży. Podaż najczęściej zmienia się w tym samym kierunku co cena, a więc przy wzroście ceny oferowane ilości rosną, natomiast przy spadku ceny maleją. Podobnie jak w [przypadku popytu interesuje z jak wrażliwa jest podaż na zmianę ceny. Informuje o tym elastyczność cenowa podaży.

Elastyczność cenowa podaży (ang. price flexibility of the supply)

Cenową elastyczność podaży definiujemy jako stosunek względnej( procentowej zmiany podaży do względnej (procentowej) zmiany ceny. Mierzy ją wskaźnik elastyczności cenowej, którego wartość obliczamy według następującego wzoru:

Es = ΔQs/Qs:ΔC/C

gdzie:
Es - współczynnik cenowej elastyczności podaży,

Qs - wielkość podaży danego dobra w okresie wyjściowym,

ΔQs - zmiana wielkości podaży danego dobra pod wpływem zmiany jego ceny,

C- cena dobra w okresie wyjściowym,

ΔC - zmiana ceny, czyli różnica między nową ceną dobra a jego ceną w okresie wyjściowym.

Formuła ta jest identyczna z formułą elastyczności cenowej popytu, przez C oznaczyliśmy cenę sprzedaży natomiast przez Qs oznaczyliśmy ilość oferowane przez dostawców. Podobnie możemy wyznaczać i analizować elastyczność podaży wzglę­dem innych (poza ceną) czynników określających wielkość podaży

Wartości i znak wskaźnika

Podobnie jak w przypadku popytu ta sama procentowa zmiana ceny może powodować różne procentowe zmiany oferowanych ilości, zatem wartość wskaźnika może być różna

Niska wartość wskaźnika elastyczności wskazuje, że podaż słabo reaguje na zmianę ceny Nawet duże zmiany ceny nie wpływaj istotnie na decyzje producentów. Gdy wartość wskaźnika jest wysoka, to nawet niewielka zmian cen wywołuje silne reakcję w postaci dużego wzrostu produkcji

Jeżeli więc wzrost ceny o 10% spowoduje zwiększenie oferowanej ilości o 25%, to elastyczność cenowa podaży wyniesie:

Es = 25%: 10% = 2,5

Jeśli wzrost ceny o 10% spowoduje zwiększenie oferowanej ilości tylko o 5%, to wartość wskaźnika elastyczność cenowa podaży wyniesie:

E s= 5%: 10% = 0,5.

Jeżeli natomiast wzrost ceny o 10 % powoduje wzrost podaży również o 10%, to wskaźnik elastyczności podaży:

Es= 10%: 10%= 1

W pierwszym przypadku, gdy Es > 1), mówimy, że podaż jest elastyczna W drugim, gdy Es< 1 mówimy, że podaż jest nieelas­tyczna. W trzecim, gdy Es=1 mówimy, że ma elastyczność jednostkową

Elastyczność funkcji a elastyczność na funkcji podaży

Przyjmijmy, że typowe funkcje podaży przyjmują postać linii prostej Podobnie jak w analizie elastyczności popytu musimy odróżniać elastyczność na krzywej (łukową lub punktową) od elastyczności całej krzywe.

Rysunek Elastyczność cenowa a rodzaj liniowej funkcji podaży

C

S1 S2 S3

C1

C0

Qs0 Qs1 Qs2 Qs3

Zbadajmy najpierw, jakie wielkości przyjmuje wskaźnik elastyczności podaży przy cenie, Co dla funkcji wychodzącej z początku układu, dla funkcji przecinającej oś odciętych (Qs) i dla funkcji przecinającej oś rzędnych (C) powyżej zera Dla lepszego wyjaśnienia posłużymy się poniższym rysunkiem

Na rysunku powyżej widzimy trzy krzywe podaży. W przedziale cen C0 - C1 Krzywa S2 jest bardziej elastyczna niż krzywa S1, krzywa S3 bardziej niż S2 bowiem gdy cena wzrasta z C0 do C1, przyrost podaży na krzywej S1 (z Qs0 do Qs2 ) jest większy niż na krzywej S1 (z Qs0 do Qs1) Ta sama zależność wystąpi w dowolnym przedziale cen Wynika z tego ,że wartość wskaźnika elastyczność zależy od położenia krzywej podaży w układzie współrzędnych

Krzywa o elastyczności zawsze większej od jedności

Jeżeli przyjmiemy liniowy charakter zależności, to krzywą podaży elastyczną na całej swej długości przedstawia linia prosta, SS, która przecina, jak na poniższym rysunku, pionową oś układu współrzędnych powyżej początku układu.

Rys. Krzywa podaży o elastyczności większej od jedności

C

S=f(C)

C1

α ΔC

C0

ΔQ

α ) β ) Qs

Qs0 Qs₁

Aby to uzasadnić podobnie jak w analizie popytu przekształcimy standardową formułę elastyczność

ΔQs ΔC

Es= ---------: --------

Qs C

do bardziej w tym momencie przydatnej postaci jak poniżej

Stałe nachylenie liniowej krzywej podaży mierzy tg α=ΔC/ΔQs Z kolei wyrażenie ΔQs/ΔC to nic innego tylko odwrotność stałego nachylenia krzywej, czyli ctg α lub inaczej ΔQs/ΔC=1/tg α Wartość tego wyrażenia jest stała na całej długości funkcji. Wyrażenie z prawej strony C/Qs =tg β to stosunek ceny do oferowanych ilości. Jego wartość zmienia się wraz ze wzrostem podaży a dokładnie maleje .

Używając symboli trygonometrycznych wskaźnik elastyczności podaży ·możemy zapisać w postaci, poniższej formuły

Es= tg β *ctg α = tg β/tg α

Ponieważ na całej długości funkcji kąt β > α zatem ma również zawsze miejsce nierówność tg β> tgα , a to oznacza, że elastyczność cenowa podaży Es= tg β/tg α jest na całej długości funkcji większa od jedności.

Zauważmy, że ponieważ w miarę wzrostu podaży kąt β maleje, zatem wartość współczynnika elastyczności podaży maleje asymptotycznie do jedności.

Krzywa o elastyczności zawsze mniejszej od jedności

Z podaż nieelastyczną mamy do czynienia, gdy procentowa zmiana wielkości podaży jest mniejsza od procentowej zmiany ceny, czyli współczynnik Es < 1.

Nieelastyczną na całej swej długości krzywą podaży w postaci linii prostej przedstawia krzywa podaży SS, która zaczyna swój bieg (lub jej przedłużenie) z poziomej osi układu współrzędnych na prawo od początku układu współrzędnych.

Rys Funkcja liniowa o elastyczności mniejszej od jedności

C

S=f(C)

C1

α)

C0

β ) α) Qs

Qs0 Qs1

Na całej długości tak skonstruowanej ·krzywej tg β< tg α, a to oznacza, że mierzony z ich pomocą wskaźnik elastyczności cenowej popytu Es= tg β/ tg α) < 1

Zauważmy dalej, że ponieważ wraz ze wzrostem podaży rośnie tg β natomiast ·tg α pozostaje niezmieniony, zatem współczynnik elastyczności podaży rośnie asymptotycznie do jedności

Krzywa o stałej elastyczności jednostkowej

Podaż o elastyczności jednostkowej ilustruje linia prosta wychodząca z początku układu niezależnie do tego, pod jakim kątem jest ona nachylona

C C

S

C1

S

C0 C1

C0

α) α)

Qs0 Qs1 Qs0 Qs1

Elastyczność na krzywej o rosnącym nachyleniu

W okresie krótkim krzywa podaży ma tradycyjny kształt linii nachylonej dodatnio, a to znaczy, że podaż zmienia się w tym samym kierunku co cena. Jednak krzywa podaży nie jest linią prostą jak na rysunku po lewej stronie, tylko staję się, jak to przedstawiono po prawej stronie poniższego rysunku coraz bardziej stroma.

Rys. krzywa podaży w okresie krótkim

C S C S

C1 ΔC

C0

ΔQs

Qs Qs

Qs0 Qs1 Qs0 Qs1

Taki kształt krzywej jest związane ze wzrostem kosztów dodatkowej produkcji, czyli kosztów krańcowych. Aby firmy chciały wytworzyć dodatkową produkcję jednakowym przyrostom produkcji towarzyszyć musi coraz większy przyrost ceny. Im bardziej rosną koszty, tym bardziej muszą rosnąć ceny, podczas gdy produkcja i podaż rosną, ale wolno Wynika z tego, że w krótkim okresie krzywa podaży ma nachylenie dodatnie, które w dodatku rośnie

Rys Krótkookresowa krzywa podaży

C

S

C2

C1

C0

Qs0 Qs1 Qs2

Im mniejsza produkcja, tym łatwiej przedsiębiorstwa zwiększają produkcję i podaż w odpowiedzi na wzrost ceny. Im bardziej płaska jest mierząca nachylenie krzywa tym bardziej elastyczna jest podaż. Ale kolejne jej wzrosty wymagają coraz większego wzrostu ceny, a to oznacza, ze podaż jest coraz mniej elastyczna.

Zależności te ilustruje zamieszczona powyżej krótkookresowa krzywa podaży SS dowolnej firmy. Przyjmijmy, że w punkcie wyjścia cenie C0 odpowiada podaż równa Qs0. Zwiększenie podaży do poziomu Qs1 wymaga wzrostu ceny do poziomu C1.

Efekty mnożnikowe, czyli jak wykorzystuje się szeregi

W ekonomii mamy często do czynienia z się efektami kumulującymi o charakterze mnożnikowym Na początek wyjaśnimy skąd się one biorą, jak przebiegają a następnie pokażemy jak można obliczyć siłę zachodzących w gospodarce zmian

Zacznijmy schematycznego przykładu pokazującego związek, jaki w warunkach niepełnego wykorzystania zdolności wytwórczych zachodzi miedzy zmianami poziomu wydatków inwes­tycyjnych a ruchem innych wielkości gospodarczych, takich jak poziom zatrudnienia i produkcji oraz dochodów i konsumpcji. Aby uniknąć nieporozumień, przyjmujemy, że inwestycje występują tu jedynie jako jeden z wydatków kształtujących łączne wydatki w gospodarcze Naszym zadaniem jest wytłumaczyć, dlaczego jeśli wydatki inwestycyjne wzrosną o pewną wielkość, to łączne wydatki wzrosną o dużo większą kwotę, czyli w sposób mnożnikowy. Przyjmiemy następujące założenia i dane wyjściowe:

1) gospodarka składa się z dwóch działów: dział I wytwarza dobra inwestycyjne, dział II produkuje dobra konsumpcyjne.

2) w obu działach występuje niepełne wykorzystania zdolności wytwórczych

3)) wychodzimy z ogólnego założenia, że całe zarobione w wyniku produkcji dochody Y są albo wydane na dobra konsumpcyjne K bądź oszczędzane Os co zapisujemy Y=K+Os, wszelki przyrost dochodu ΔY rozkłada się na ΔY=ΔK+ΔOs

4) zagregowana przeciętna stopa konsumpcji to stosunek wydatków konsumpcyjnych do całości dochodu K/Y

5) zagregowana krańcowa stopa konsumpcji, wskazująca, jaka część przyrostu dochodu jest wydatkowana na konsumpcję c=ΔK/ΔY. Natomiast zagregowana krańcowa stopa oszczędzania to s=ΔOs/ΔY

6 ) Ponieważ ΔY=ΔK+ΔOs zatem ΔY/ΔY=ΔK/ΔY+ΔOs/ΔY=1 a to oznacza że c+s =1

6) przyjmiemy, że krańcowa stopa konsum[opcji wynosi c=2/3 i jest równa przeciętnej stopie konsumpcji W tej sytuacji krańcowa stopa oszczędzania s= 1- 2/3= 1/3

7) w badanym okresie decyzje (zamówienia) inwestycyjne są takie, że wydatki inwestycyjna I w okresie t + 1 wzrosły w stosunku do okresu t o ΔI= 120 mld jednostek pieniężnych np. dolarów

W tej sytuacji w dziale I zwiększa się wykorzystanie aparatu produkcyjnego oraz zatrudnienie i w efekcie rośnie produkcja dóbr inwestycyjnych. Wartość przyrostu produkcji finalnej odpowiada przyrostowi dochodów brutto w tym dziale (tj. przyrostowi płac i zysków brutto na łączną sumę 120 mld dolarów. Ten przyrost, który nazwiemy roboczo pierwotnym wzrostem dochodu(zysków brutto i płac), jest równy:

ΔY0= ΔI=120

Część tego pierwotnego wzrostu dochodu zostaje przeznaczona na zakupy konsumpcyjne a część zostania zaoszczędzona. Zwiększone zapotrzebowanie na dobra konsumpcyjne może być zrównoważony dodat­kową produkcją dóbr konsumpcyjnych, ponieważ w dziale II istnieje niewykorzystany aparat wytwórczy, a na rynku pracy — nie zatrudnieni robotnicy.

Dodatkowa produkcja sprzedaż środków konsumpcji wygeneruje dodatkowe dochody, czyli płace i zyski w dziale wytwarzającym środki konsumpcji Dochody te powiększą zapotrzebowanie na dobra konsumpcyjne

Obliczmy zatem o ile wzrośnie popyt konsumpcyjny a w efekcie i odpowiadający mu przyrost dochodów brutto w dziale II Jego wysokość zależy jednocześnie od pierwotnego wzrostu ΔY1 dochodu oraz stopy konsumpcji, a więc wynosi.:

ΔY1= 120 *2/3=80

Ten wzrost możemy nazwać wtórnym wzrostem dochodu; co symbolicznie zapiszemy jako:

ΔY1= ΔI*c

Następnie część wtórnego wzrostu dochodu częściowo jest oszczędzana a częściowo kierowana na dalsze zakupy dóbr konsumpcyjne W warunkach ciągle nie w pełni zatrudnionych czynników produkcji spowoduje kolejny przyrost produkcji i dochodów w dziale II Jest to już wzrost trzeciego szeregu i wynosi on odpowiednio:

ΔY2= 120 * 2/3* 2/3 = 120 * (2/3) ²

Co ogólnie zapisujemy jako:

ΔY2= ΔI*c²

Ponadto ma miejsce kolejny przyrost dochodu:

ΔY3= 120* c³

Co ogólnie zapisujemy:

ΔY3 = ΔI*c³

Przyrostów tych może być „ n”, ostatni z nich wynosi:

ΔYn = ΔI*cⁿ

Aby obliczyć łączny przyrost produkcji i dochodu w okresie musimy zsumować przyrosty cząstkowe:

ΔY t+1 = 120 +120*2/3+120*(2/3)² +120*(2/3) ³+ 120*(2/3) ⁿ

Natomiast w wyrażeniu symbolicznym:

ΔYt+1 = ΔI + ΔI *c+ ΔI *c²........+ ΔI *cⁿ

Jeśli wyciągniemy przed nawias120 to otrzymamy:

ΔYt+1 = 120 [1 + 2/3)^{2 +} 2/3)³ + …+(2/3) ⁿ ]

Ogólnie zapisujemy to jako:

ΔYt+1= ΔI [1+c+c² +c³+.... +cⁿ ]

Algebraiczna wartość sumy wyrażeń zawartych w nawiasie kwadratowym wynosi:

1 1

[1+c+c² +c³+.... +cⁿ ] = -------- = -------

1- c s

Zauważmy dalej, ze jeśli 1>c>0, to ko1ejne przyrosty wydatków i dochodów ΔY stają się coraz mniejsze, dążąc do zera tworzą nieskończony postęp, sumę jego wyrażeń można obliczyć można posługując się formułą algebraiczną:

1

ΔY t+1= ΔI * --------

1 - c

Zauważmy, że tak obliczony przyrost dochodu jest większy od przyrosty inwestycji

ΔY t+1> ΔI

Wynika z tego, że:

ΔY t+1

------- >1

ΔI

Oznacza to, że łączny przyrost dochodu stanowi wielokrotność przyrostu wydatków inwestycyjnych

Wykorzystamy to spostrzeżenie, aby do naszej skrzynki z narzędziami wprowadzić nowe bardzo użyteczne w dalszych analizach pojęcie zwane mnożnikiem wydatków inwestycyjnych, który oznaczymy symbolem mi

Mnożnik inwestycyjny

Mnożnik to swojego rodzaju współczynnik określający rozmiary krańcowego wpływu, jaki wywiera zmiana jednej wielkości ekonomiczna na drugą, której ta pierwsza jest składnikiem. Relacja ta informuje nas, w jakiej proporcji wzrośnie dochód w stosunku do danej zmiany wielkości wydatków inwestycyjnych W naszym przykładzie dochód narodowy brutto powiększył się liczbowo jak następuje

ΔY t+1= mi * ΔIt

Gdzie wartość mnożnika to

1 1

mi = [1+c+c² +c³+.... +cⁿ ] = -------- = -------

1- c s

W ten sposób otrzymaliśmy symboliczny zapis mnożnika wydatków inwestycyjnych. Jak pamiętamy c+s=1 zatem 1-c =s , wynika z tego że mnożnik alternatywnie możemy zapisać jako 1/s.

Mnożnik inwestycyjny jest ilościowym ujęciem zjawiska pobudzania (bądź ograniczania) wydatków konsumpcyjnych za pomocą zmian poziomu wydatków inwestycyjnych. Dochody powstałe w trakcie wzrostu produkcji dóbr inwestycyjnych zwiększają popyt na dobra konsumpcyjne, co z kolei powoduje wzrost produkcji dóbr konsumpcyjnych i dodatkowe dochody, powiększające popyt konsumpcyjny. Jeżeli mnożnik wynosi mi, to zmiana poziomu wydatków inwestycyjnych równa ΔI wywoła zmianę poziomu dochodu narodowego o wielkość równą ΔI *mi, co stanowi wielkość popytowego efektu wydatków inwestycyjnych.

Jest to mnożnik Keynesowski, ale autorem, który pierwszy (w 1931 r.) wprowadził koncepcje mnożnika do teorii ekonomii, był jego uczeń R. F. Kahn Badając z inspiracji Keynesa wpływ robot publicznych na poziom działalności gospodarczej Kahn dowiódł, iż wzrost zatrudnienia przy robotach publicznych (zatrudnienie pierwot­ne) powoduje „mnożenie się” zatrudnienia w całej gospodarce. Jest tak, bo dodatkowe zatrudnienie —przez wzrost funduszu płac i popytu konsumpcyjnego — pociąga za sobą kolejne przyrosty zatrudnienia w gałęziach dóbr konsumpcyj­nych (zatrudnienie wtórne). Ilościowa relacja miedzy całkowitym wzrostem zatrudnienia a wzrostem zatrudnienia przy robotach publicznych, czyli relacja między całkowitym wzrostem zatrudnienia (pierwotne plus wtórne) a zatrudnieniem przy robotach publicznych określona została mianem mnożnik zatrudnienia,

Keynes przejął koncepcję mnożnika zatrudnienia by przedstawić ilościowy związek, który w warunkach niepełnego wykorzystania zdolności wytwórczych zachodzi między zmianami poziomu wydatków inwestycyjnych (ΔI) a zmianami rozmiarów globalnego popytu i dochodu narodowego (ΔY). Inwestycje w jego koncepcji występują tylko w roli czynnika kształtującego popyt.

W naszym przykładzie wartość mnożnika wydatków wynosi mw=3. Oznacza to, że wzrost wydatkowa inwestycyjnych o 120 dol wygenerował trzykrotnie większy wzrost dochodu.

ΔY t+1= mw* ΔI

ΔY t+1=120*3=360mld

Mechanizm mnożnika działa nie tylko „w gorę”. Jeśli wydatki inwestycyjne w t+1 są mniejsze niż w t (np ΔI=-120 mld dol.), to mechanizm mnożnika działa ,,w dół” i daje zwielokrotniony spadek globalnego popytu i dochodu narodowego (-120 mld dol*3=-360).

METODY I NARZĘDZIA STATYSTYKI

Wiele dziedzin nauki zajmuje się obserwacją otaczającego nas świata lub też posługuje się eksperymentem dla potwierdzenia swoich teorii. Takie badanie przebiega zazwyczaj według schematu: zebranie dużej ilości danych, ich analiza i interpretacja. Badaczowi potrzebny jest wtedy zestaw narzędzi - sprawdzonych metod, które umożliwią mu operowanie na dużych zbiorach danych. Tworzeniem i rozwijaniem takich użytecznych narzędzi zajmuje się właśnie statystyka. Statystyka przy pomocy danych liczbowych opisuje wszystkie najważniejsze dziedziny naszego życia.

Statystyka dostarcza metod i narzędzi opisu poszczególnych kategorii ekonomicznych, które umożliwiają przedstawienie rzeczywistość gospodarczą w formie liczb. Ma to olbrzymie znaczenie przy pomiarze natężenia różnych procesów i ich zmiany w czasie. Dzięki statystyce, wiemy, jak żyje przeciętny obywatel, czyli dowiadujemy się, jakie otrzymuje wynagrodzenie, ile wypija mleka, jakiej wielkości posiada mieszkanie, jak często chodzi do kina.

Statystyka to nauka, której przedmiotem zainteresowania są metody pozyskiwania, prezentacji, a przede wszystkim analizy danych opisujących zjawiska masowe. Jak podaje encyklopedia PWN pochodzące z łaciny pojęcie statystyka ma przynajmniej dwa znaczenie

1) Numeryczne dane dotyczące agregatów złożonych z pewnych jednostek.

2) Nauka zajmująca się zbieraniem, analizą i interpretacją tego typu danych.

W pierwszym znaczeniu statystyka jest utożsamiana z bazami danych liczbowych o obserwowanych zbiorowościach jednostek oraz o ich cechach statystycznych. W drugim obecnie jest utożsamiana z komputerowym przetwarzaniem baz danych liczbowych w postać ich syntetycznych charakterystyk liczbowych oraz w postać wnioskowania statystycznego w warunkach niepewności.

W ujęciu ogólnym statystyka jest więc dyscypliną nauki, która zajmuje się formułowaniem metod liczbowego przetwarzania indywidualnych informacji statystycznych w celu opisu i wnioskowania statystycznego. To ostatnie zajmuje się głównie procedurami estymacji (szacowania) parametrów oraz weryfikacji hipotez zerowych

Celem stosowania statystycznych metod opisu i wnioskowania jest stworzenie możliwości przeprowadzania rzetelnej diagnostyki statystycznych (jak jest i dlaczego tak jest) oraz wysoce prawdopodobnej predykcji statystycznej (jak by było przy spełnieniu określonych warunków?). Diagnostyka i predykcja statystyczna są określane jako analiza statystyczna.

Statystyka ma rozległe zastosowanie wszędzie tam, gdzie występują zjawiska i procesy masowe. Badając zjawiska masowe (np. produkcję, zatrudnienie, płace, wzrost) obserwuje się w rzeczywistości zdarzenia losowe, których rozmiary liczbowe (realizacje zmiennych losowych) podlegają zarówno działaniu przyczyn głównie (wywołujących zmienność systematyczną), jak i ubocznych (wywołujących zmienność przypadkową). Stosowanie określonych metod statystycznych (opisu i wnioskowania) na określonym polu ich użyteczności (struktura, korelacja, dynamika) umożliwiło powstanie specjalistycznych dyscyplin statystyki stosowanej, np. statystyki ekonomicznej, statystyki społecznej, statystyki medycznej, statystyki fizycznej, statystyki ludności

Krótka historia statystyki

( Hasła W Encyklopedii PWN)

Pierwotnie termin statystyka był używany na oznaczenie wiedzy o państwie. Swoje początki statystyka wywodzi z tradycji dokonywania spisów powszechnych, czyli zbierania informacji na temat ludności Poczynając od najdawniejszych spisów w Egipcie i Chinach, poprzez rzymskie cenzusy (spisy) i średniowieczne inwentaryzacje majątków feudalnych i kościelnych, najpierw słowny, a potem liczbowy spis statystyczny służył głównie jako narzędzie w rękach władców i rządów państw. Z pewnością posiadanie informacji na temat stanu ludności ułatwiało rozpoznawanie trendów i odpowiednie planowanie. Ślady pierwszego spisu można znaleźć w Księga Księdze Liczb, kiedy to Mojżesz wyprowadzał lud Izraela z Egiptu. Spisy powszechne, co potwierdza Nowy Testament, były również stosunkowo systematycznie przeprowadzane na terenie starożytnego Rzymu.

Prekursorami szerszego traktowania statystyki byli tzw. arytmetycy polityczni, a zwłaszcza w XVII w. wybitni przedstawiciele tego kierunku — J. Graunt i W. Petty). Posługując się stosunkowo prostymi narzędziami opisu statystycznego arytmetycy polityczni wykazywali, że w pozornie chaotycznych, przypadkowych zjawiskach masowych występują określone regularności (prawidłowości) Pozwoliło to sformułować pierwsze proste uogólnienia teoretyczne dotyczące statystyki (K. Davenant, 1695).Dzięki zapoczątkowaniu ery tabelaryzmu i arytmetyki politycznej, powstał pierwszy uściślony tabelaryczny opis Rosji z 1726-27 (J.K. Kirgiłow) oraz Danii z 1741 (J.P. Anchersen Jeszcze w połowie XIX w. termin statystyka oznaczał podany w tabelarycznej formie zbiór danych na temat stanu państwa.

Można przypuszczać, że w pewnym momencie posiadanie podstawowych danych stało się niewystarczające, szczególnie przy coraz szybciej rozwijającej się gospodarce światowej. Konieczne stało się nie tylko ulepszanie metod pozyskiwania danych, ale również ich opisu i analizy. Zbiegło się to w czasie z szybkim rozwojem metod matematycznych, szczególnie teorii prawdopodobieństwa wyjaśniająca mechanizm, w jakim ujawniają się prawidłowości statystyczne występujące w zjawiskach masowych. Rachunek prawdopodobieństwa stał się on podstawą współczesnej statystyki.

Jego rozwój zapoczątkowali w 2 połowie XVII w. B. Pascal i P. Fermat, którzy pierwsi uzasadnili matematycznie prawidłowości występujące w grach hazardowych. Sformułowane przez nich wstępne założenia i wnioski rozwijało wielu wybitnych teoretyków zwanych probabilistami. Sa to przede wszystkim J. Bernoulli, który u schyłku XVII w. pierwszy sformułował i uzasadnił tzw. prawo wielkich liczb. Stało się ono podstawą do udowodnienia przez A. de Moivre'a (koniec XVIII w.), P.S. de Laplace'a (pocz. XIX w.) oraz J.W. Lindberga i P. Levy'ego (lata 20. XX w.) tzw. lokalnego i centralnego twierdzenia rachunku prawdopodobieństwa.

W XVIII i XIX w. powstały ważne dla statystyki odkrycia teoretyczne , związane ze statystycznymi badaniami prowadzonymi metodą reprezentacyjną. Sformułowano wzór funkcji gęstości rozkładu normalnego zmiennej losowej ciągłej oraz rozkładu błędów losowych (Laplace i K.F. Gauss). Nastąpiło wyodrębnienie składnika systematycznego i przypadkowego występujących w procesach zw. zjawiskami masowymi (Gauss) oraz określono prawo rzadkich zdarzeń (S. Poisson).

Okres od końca XIX w. charakteryzował się wielką liczbą odkryć nowych metod i procedur badań statystycznych (parametrycznych i nieparametrycznych); duży udział w tworzeniu dorobku metodologicznego statystyki mieli polscy statystycy, m.in.: M. Fisz, Z. Hellwig, J. Neyman, H.D. Steinhaus, S. Szulc.

Współcześnie szczególnie wyraźne przyspieszenie rozwoju metod i procedur statystycznych badań wiąże się z szerokim zastosowaniem technik komputerowych. Dzięki temu rozwinęła się statystyka matematyczna

Jest to dział matematyki zajmujący się metodami wnioskowania o własnościach populacji na podstawie losowych prób z tej populacji; wnioskowanie to polega na szacowaniu różnych parametrów populacji (estymacji teoria) lub na weryfikowaniu, za pomocą odpowiednich statystycznych testów, różnych hipotez o tych populacjach; pewne jednolite podejście do statystyki matematycznej proponuje teoria decyzji statystycznych; ze statystyki matematycznej wyodrębniły się wyspecjalizowane zespoły metod rozwijane jako biometria, epidemiologia, ekonometria, statystyczna kontrola jakości, teoria niezawodności i in.

Dawniej ci, którzy chcieli korzystać z metod statystycz­nych, musieli nauczyć się wielu wzorów i sposobów ich stosowania. Ponownie dopadła ich zmora szkolnych trudności z nauką matematy­ki. Dziś wszystko to można osiągnąć bez uciekania się do specjalnych metod, Choć szczegóły obliczeń mogą być interesujące i przydatne ekonomista, jeśli chce, może się obyć bez ich znajomości: komputer osobisty, a nawet zwykły kalkulator wykona tę trudną pracę za niego Dlaczego więc statystyka miałaby być aż tak przydatna

Jak już powiedziano, główne zadania ekonomisty polega na właści­wej ocenie Aby była ona trafna, nie może opierać się na przeczuciach i domysłach, lecz na faktach Najbardziej powszechnymi i użyteczny­mi faktami są liczby, które jednak poddane nieumiejętnej obróbce mogą dostarczyć błędnych informacji Wprawdzie komputer bardzo przydaje się do wykonywania obli­czeń, musi jednak otrzymać od nas właściwe dane, a jego użytkownik musi wiedzieć, co i jaką metodę obliczeniową zastosować w konkretnej sytuacji?

Statystyka jest dziedziną bardzo rozległą i większość ekonomistów korzysta tylko z jej bardzo wąskiego wycinka. Zagadnienia mające największe zastosowanie dla ekonomisty to:

• Średnie

• Indeksy

• Prawdopodobieństwo

• Rozkład statystyczny

• Regresja

• Korelacja

Aby poznać te zagadnienia i sposoby obliczania równych niezbędnych w statystyce wielkości występujących i ich zastosowania, każdy może sięgnąć po dowolny podręcznik staty­styki dla studentów zarządzania wybierając z indeksu rzeczowego wymienione wyżej zagadnienia. Ułatwimy wam to zdanie i omówimy krótko niektóre z nich.

Średnie

Posługiwanie się szczegółowymi danymi bywa niekiedy bardzo kłopotliwe ze względu na nadmiar informacji W takich przypadkach z pomocą przychodzą nam wielkości średnie

Średnia arytmetyczna

Załóżmy, że w ciągu semestru dwaj studenci (Piotr i Paweł) uzyskali z matematyki następujące oceny (w dwudziestopunktowej skali):

	Rzeczywiste oceny w punktach	Średnia arytmetyczna
Paweł	3, 12, 5, 7, 8, 5, 5, 7, 14, 5	7,1
Piotr	7 , 6, 9, 7, 10, 9, 7, 7, 11, 12	8,5

Czy Paweł osiągał lepsze oceny od Piotra? Jeżeli szereg ocen jest długi. to zebrane informacje, bez żadnego przetworzenia, nie pozwalają udzielić jednoznacznej odpowiedzi na to pytanie. Trzeba zdefiniować kryterium, za pomocą, którego można by ocenić wyniki Piotra na tle wyników Pawła. Tradycyjnie przyjmowanym kryterium jest średnia arytmetyczna - prosta lub ważona

Średnia arytmetyczna prosta

Przykład:

Dla oceny poziomu Piotra i Pawła w zakresie matematyki można przyjąć następujące rozumowanie: suma ocen Pawła wynosi 71 punk­tów a Piotra 85 punktów. Jeżeli oceny każdego ze studentów były równomiernie rozłożone między wykonane zadania, to jaką ocenę można by było przyznać każdemu z nich ?

3 +12+ 5+ 7 +8 +5 +5 + 7 + 14 + 5 71

Paweł =---------------------------------------------------= ----- = 7,1

10 10

7 + 6 + 9 +7+ 10+ 9 + 7 + 7 +11 +12. 85

Piotr =--------------------------------------------------------= ----- = 8,5

10 10

Mówimy, że średnia arytmetyczna prosta (inaczej średnia nie ważona) z ocen Pawła wynosiła 7,1, a Piotra 8,5, skąd wynika, że wyniki Piotr były przeciętnie lepsze od wyników Pawła

Średnia arytmetyczna prosta w statystyce to suma wartości wszystkich jednostek zbiorowości statystycznej podzielona przez liczebność tej zbiorowości (tj. liczbę tych jednostek). Wzór na średnią arytmetyczną ma postać:

X1+X2 +.... +Xn

Sa = ----------------------------

n

gdzie: Sa - średnia arytmetyczna, X₁,X₂,...,X_n - poszczególne wartości pojedynczych jednostek zbiorowości statystycznej, n - ogólna liczebność badanej zbiorowości (tj. liczba wszystkich jednostek wchodzących w skład zbiorowości statystycznej).

Średnia arytmetyczna ważona

W badaniach statystycznych bardzo często wyznacza się średnie arytmetyczne ważone. Załóżmy, że otrzymane oceny odpowiadają dwóm rodzajom zadań, ocenianych jako mniej ważne (wykonane w domu) lub ważniejsze (rozwiązane w czasie egzaminu).

	Zadnia domowe	Zadania egzaminacyjne	Średnia ważona
Paweł	7, 8, 5, 5, 7, 14, 5	3 ,12 , 5	6,9
Piotr	7, 9, 10 ,7, 7, 11, 12	7 , 6 , 9	8,06.

Dla rozróżnienia znaczenia obu typów zadań można im przy wyznaczaniu średniej przydzielić różne „wagi". Można na przykład przyjąć, że jedno zadanie egzaminacyjne jest równoważne trzem zadaniom domowym. Prowadzi to do dwóch rodzajów wag: 1 dla zadań domo­wych i 3 dla zadań egzaminacyjnych. Przy wyznaczaniu średniej oceny dla każdego ze studentów weźmiemy pod uwagę różne wagi przyznane obu typom zadań:

1* (7+8+5+5+7+14+5)+3*(3+12+5)

Paweł: ----------------------------------------------- = 6,9

7+3*3 = 16

Piotr: 1*(7+9+ 10+7+7+ 11 + 12)+3*( 7+6+9 )

----------- ---------------------------------------- = 8,06.

7+3*3 = 16

Przyjmujemy, więc, że studenci rozwiązali jak gdyby 16, a nie 10 zadań, gdyż jedno zadanie egzaminacyjne równe jest trzem zadaniom domowym.

Ogólny wzór na średnią arytmetyczną ważoną zapisujemy jak poniżej

X1*W1 + X2* W2 + .... Xn*Wn

Sw = ------------------------------------------------

W1 + W2 + .... Wn

Gdzie Sw- średnia arytmetyczna ważona, X1+X2+....+Xn zaobserwowane wartości zmiennych, W1+ W2 + .... Wn wagi ,(współczynniki wagowe ).Wagi mogą być definiowane w różny sposób w zależności od rodzaju badania, częstości zachodzenia pwenego zjawiska ,wolumenu, wskaźnika udziału itp

Dlaczego interesujemy się średnimi?

Synteza informacji

Odwołanie się do średniej w celu scharakteryzowania danej populacji może wynikać z faktu, iż trudno jest wyciągać wnioski na podstawie zbyt dużego zbioru nieprzetworzonych danych. („Populacja" nie musi oznaczać zbioru ludzi. Może oznaczać zbiór dowolny elementów. Np.. można mówić o populacji 5 filiżanek, do których jest 5 spodeczków przeciętna liczba spodeczków na filiżankę wynosi 1.)

Jeżeli rozpatrujemy sytuację robotników we Polsce, to informacje o ich poziomie życia, wyposażeniu w dobra trwałego użytku, liczbie ich dzieci itd.. zajmowałyby setki i tysiące stron, podczas gdy wykorzystanie średniej pozwala opisać sytuację gospodarczą tej grupy społecznej za pomocą kilku liczb. Podobnie porównanie wielu różnych populacji na podstawie nieprzetwo­rzonych danych może sprawiać duże trudności, podczas gdy zestawienie wartości średnich pozwala wyciągnąć natychmiastowe wnioski.

Pułapki związane ze średnią arytmetyczną

Średnia arytmetyczna pomija rozproszenie danych

Inna cecha -średniej arytmetycznej, która jest przyczyną licznych błędów, wynika ze sposobu jej konstrukcji, który nie ujawnia roz­proszenia wartości składających się na średnią.

Powróćmy do przykładu wyznaczania prostej średniej arytme­tycznej na podstawie ocen z matematyki uzyskanych przez studenta Pawła.

Osoby	Oceny rzeczywiste	Oceny abstrakcyjne
Paweł	3, 12, 5, 7, 8, 5, 5, 7, 14, 5	7,1
Piotr	7 , 6, 9, 7, 10, 9, 7, 7, 11, 12	8,5

Rachunek sprowadza się do znalezienia takiej oceny, którą otrzymałby Paweł za każde z zadań, gdyby suma uzyskanych przez niego ocen równomiernie rozłożyła się między wszystkie rozwiązy­wane przez niego zadania. Przechodzimy więc od sytuacji A do sytuacji B. Na rysunku B różnice między ocenami z poszczególnych zadań znikają. Jeżeli odchylenia od wartości średniej są niewielkie, to wartość informacyjna średniej arytmetycznej jest duża; jeżeli są jednak duże, to część informacji zostaje pominięta.

Rys A oceny rzeczywiste Pawła Rys B oceny abstrakcyjne

14 14

13 * 13

12 * 12

11 11

10 10

9 9

8 * 8

7 * * 7 * * * * * * * * * *

6 6

5 * * * * 5

4 4

3 * 3

2 2

1 1

0

1 2 3 4 5 6 7 8 9 10 1 3 4 5 6 7 8 9 10

numer zadania numer zadania

Średnie arytmetyczne to wielkości, które nie mają rzeczywistych odpowiedników

Przeciętna liczba dzieci w rodzinach mieszkających w moim domu, wynosi 1,7, a każde mieszkanie zajmowane jest przez 3,6 osoby Można podać wiele przykładów takich wartości średnich, które nie mają rzeczywistego odpowiednika. Jeżeli razi nas ta nonsensowna, na pierwszy rzut oka, wartość cechy to dlatego, że zapominamy o tym, że celem tego miernika nie jest odzwierciedlenie pojedynczych przy­padków, lecz podanie pewnej ogólnej charakterystyki danej sytuacji.

Niemniej jednak podane przykłady świadczą o tym, że średnia arytmetyczna nie musi być wielkością najczęściej występującą

Średnia a przypadek indywidualny

Weźmy inny przykład, załóżmy, że dysponujemy następującymi infor­macjami:

• przeciętny dochód w populacji A wynosi 1000 zł na miesiąc.

• przeciętny dochód w populacji B wynosi 2000 zł na miesiąc.

Czy można na tej podstawie stwierdzić, że osoba należąca do populacji B ma dochód w przybliżeniu dwukrotnie większy od do­chodu osoby należącej do populacji A? Innymi słowy czy średnia arytmetyczna z dochodów odzwierciedla sytuację poszczególnych członków grupy? Odpowiedź na to pytanie wymaga dodatkowych informacji na temat składu każdej grupy.

Przyjmijmy dwa założenia, co do rozłożenia dochodów w populacji A i B.

Założenie 1:

Populacja A1	Populacja B1
Osoba 1 zarabia 1000	Osoba 1 zarabia 2000
Osoba 2 zarabia 1100	Osoba 2 zarabia 1900
Osoba 3 zarabia 900	Osoba 3 zarabia 2100
Osoba 4 zarabia 1000	Osoba 4 zarabia 2000

Przeciętny zarobek 1 000 Przeciętny zarobek 2 000

Założenie 2:

Populacja A2	Populacja B2
Osoba 1 zarabia 1000	Osoba 1 zarabia 10
Osoba 2 zarabia 1000	Osoba 2 zarabia 10
Osoba 3 zarabia 1000	Osoba 3 zarabia 10
Osoba 4 zarabia 1000	Osoba 4 zarabia 7970

Przeciętny zarobek 1 000 Przeciętny zarobek 2 000

Jeżeli przy założeniu 1 można rzeczywiście powiedzieć, że osoby z populacji B1 mają blisko dwukrotnie większe dochody niż osoby należące do populacji A1, to przy założeniu 2 jest to oczywisty fałsz. Trzy spośród czterech osób populacji B2 zarabiają sto razy mniej niż osoby z populacji A2, a jedna osoba z populacji B2 zarabia 7,97 razy więcej niż dowolna osoba z populacji A2. Oznacza to, że przy założeniu 1 średnia z dochodów w trafny sposób odzwierciedla sytuację każdej osoby należącej do populacji A1 i B1. Natomiast przy założeniu 2, odbiega ona daleko od opisu konkretnych sytuacji osób z populacji B2. Nie odpowiada ona sytuacji najbiedniejszych, których dochody są 200 razy mniejsze od wartości przeciętnej, ani też sytuacji osoby najbogatszej, której dochody są cztery razy wyższe niż dochód średni.

Inne centralne miary statystyczne

Dla porównania poziomu ocen z matematyki każdego ze studentów, można przeprowadzić inny rodzaj rozumowania niż ten, który przyjęto stosując średnią arytmetyczną, rozumianą jako kryterium oceny wiedzy.

Przyjmiemy, że obaj studencki przechodzili 10 testów Uzyskana z nich oceny zostały uporządkowane w poniższej tabeli według wysokości

	50 % ocen	50 % ocen	Dominanta	Mediana	Średnia arytmetyczna
Piotr	6, 7 , 7, 7, 7,	9, 9, 10, 11, 12	7	8	75:10 = 7,5
Paweł	3, 5, 5, 5, 5,	7, 7, 8, 12, 14	5	6	71:10 = 7,1

Średnia modalna (moda, dominanta)

Można na przykład postawić pytanie, jaka ocena uzyskiwana była przez obu studentów najczęściej? Jest to pytania o wartość modalną zwaną krótko modą lub dominantą, czyli najczęściej obserwowana wartość badanej cechy.

Liczba zadań Pawła

10

9

8

7

6

5

4 *

3 *

2 * *

1 * * * * *

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Otrzymana ocena

dominanta (moda ) mediana

Mediana

Można również oceniać poziom każdego studenta przypisując mu ocenę zwaną medianą (wartość środkowa), która dzieli zbiór zadań na dwie równoliczne grupy w taki sposób, że liczba zadań, za które student otrzymał niższe oceny, jest równa liczbie zadań, za które student otrzymał oceny wyższe od tej oceny.

Mediana odpowiada takiej wartości cechy Me. że liczba obserwacji mniejszych od Me jest równa liczbie obserwacji większych od Me

Mediana (zwana też wartością środkową lub drugim kwartylem) to w statystyce wartość cechy w szeregu uporządkowanym, powyżej i poniżej której znajduje się jednakowa liczba obserwacji.

W celu wyznaczenia mediany trzeba uporządko­wać wyniki obserwacji w rosnącym porządku

Aby obliczyć medianę ze zbioru n obserwacji, sortujemy je w kolejności od najmniejszej do największej i numerujemy od 1 do n Następnie, jeśli n jest nieparzyste, medianą jest wartość obserwacji w środku (czyli obserwacji numer (n+1)/2). Jeśli natomiast n jest parzyste, wynikiem jest średnia arytmetyczna między dwiema środkowymi obserwacjami.

W naszym przykładzie Piotr najczęściej, bo cztery raz otrzymał ocenę 7 W języku statystycznym średnia modalna dla Piotra wynosiła „7" Z kolei Paweł najczęściej, bo trzy razy otrzymał ocenę „5" Według kryterium średniej modalnej Piotr otrzymuje lepsze oceny niż Paweł

W przy­padku Piotra 50 procent jest niższych od 8 a 50 % wyższych od 8 Medianą z jego ocen jest „8" W przypadku Pawła 50% ocen jest niższych od 6 i 50% jest wyższych od 6. Innymi słowy medianą z ocen Pawła jest „6". Zgodnie z tym kryterium wyniki Piotra są lepsze od wyników Pawła

Niekiedy używane są też inne wersje mediany:

* Wersja, w której dla parzystego n zamiast średniej arytmetycznej losuje się jedną z dwóch obserwacji: numer Taka mediana nie wyprowadza wyniku poza zbiór dotychczasowych wartości.

* Mediana ważona, w której każda obserwacja ma przypisaną wagę

Którą z miar centralnych należy wybrać?

Wybór centralnej miary statystycznej zależy od tego, co chcemy pokazać. Mediana znalazła szerokie zastosowanie w statystyce jako średnia znacznie bardziej odporna na elementy odstające niż średnia arytmetyczna Jest to na ogół zaletą, choć czasem może być uważane za wadę szczególnie wtedy, gdy występują niw wpływające na jej wartość duże rozpiętości skrajnych obserwacji.

Średni dochód może być istotnym wskaźnikiem poziomu życia, jeżeli dochody nie są zbyt rozproszone w stosunku do średniej arytmetycznej. Dochód modalny odpowiada dochodowi i uzyskiwanemu najczęściej przez osoby tworzące daną populację i in­formuje o najczęściej spotykanej sytuacji. A dochód medialny in­formuje o minimalnym dochodzie, jaki osiąga bogatsza połowa osób. a także o dochodzie maksymalnym uzyskiwanym przez biedniejszą połowę osób.

Gdybyśmy mogli wy­brać kraj zamieszkania, w którym dochód przydziela się losowo z ogólnej pu­li dochodów istniejących w tym kraju, to czy wybralibyśmy kraj o najwyższym PKB na obywatela, czyli dochód średni? Nie znacznie większe zna­czenie miałaby dla was dochód medianowy, czyli wartość dzieląca daną populację na pół 50 proc. ludzi zarabia poniżej tej su­my, a 50 proc. powyżej. W miarę jak krzywa dystrybucji dochodów staje się coraz bardziej stroma, gdyż coraz większa część bogactwa znajduje się w rękach wą­skiej elity, mediana dochodów coraz bar­dziej spada poniżej średniej. Dlatego też np. w USA rośnie wprawdzie PKB na głowę, ale dochód medianowy na gospodarstwo domowe w rzeczywistości spada.

Pomiar nierówności

Ekonomia, jak również inne nauki społeczne, od dawna interesują się kwestią podziału dochodu w społeczeństwie i jego determinantami oraz analizują źródła powstających na tym tle nierówności.

W połowie 1998 r. przeciętne miesięczne wynagrodzenie nominalne brutto w Polsce wynosiło 1221 zł, a wynagrodzenie netto - 1021 zł. Po tzw. ubruttowieniu zarobków, w styczniu 1999 r. przeciętne wynagrodzenie brutto (powiększone o obowiązkową składkę na ubezpieczenia społeczne) wyniosło 1345 zł.

Wielkości przeciętne zacierają ogromne różnice w zarobkach różnych osób. Możliwe są bowiem sytuacje w których niewielka grupa gospodarstw domowych otrzymuje wysokie dochody zaś pozostałe, liczne gospodarstwa mają znikomy udział w globalnym dochodzie. Aby poznać sytuacje materialną pracowników, trzeba się zapoznać z rozkład dochodów.

Do prawidłowego zrozumienia ważnych kwestii dotyczących poziomu rozwoju społecznego i gospodarczego społecznego pokoju itd. niezbędne jest znajomość rozkładu dochodów w społeczeństwie Zagadnieniami tymi żywo zainteresowana jest także szeroko rozumiana opinia publiczna. We wrześniu 1997 r. rozkład miesięcznych zarobków brutto był następujący:

Rozkład zarobków w Polsce w 1997r
Przedział zarobków	Odsetek pełnozatrudnionych
do 500 zł	7,6%
500-700 zł	18,0%
700-900 zł	20,4%
900-1200 zł	23,1 %
1200-1500 zł	12,8%
1500-2000 zł	9,6%
powyżej 2000 zł	8,5%

Krzywa Lorenza

Szeroko stosowaną metodą analizy nierówności dochodowych i majątkowych w społeczeństwie jest tzw. krzywa Lorenza. Jest to narzędzie pozwalające w sposób wizualny przedstawić stopień nierówności w rozkładzie dochodów pomiędzy skrajnymi przypadkami. Krzywa ta pokazuje ona, jaka część dochodu (majątku) całego społeczeństwa przypada w udziale wyróżnionym według stopnia zamożności grupom badanych gospodarstw domowych. Aby ją wykreślić badaną populację dzieli się na kilka np. cztery (kwartyle), pięć (kwintyle), a niekiedy dziesięć (decyle) równych liczebnie grup gospodarstw domowych, Następnie porządkujemy je od najuboższych do najzamożniejszych. Sumując (kumulując) dochody w kolejnych grupach można porównać faktyczny rozkład dochodów z przypadkami skrajnymi.

Rozkład pracowniczych dochodów gospodarstw oraz dochodów gospodarstw chłopskich w Polsce w roku 1992
Kolejne 10% grupy dochodowe	Skumulowany procent gospodarstw	Procentowy udział gospodarstw pracowniczych w dochodzie	Procentowy udział gospodarstw chłopskich w dochodzie	Skumulowany procent dochodu
								Absolutna Absolutna Stan rzeczywisty Stan równość nierówność gospodarstwa rzeczywisty pracownicze chłopskie
Najniższe 10	10	4,1	3,2	10 0 4,1 3,2
Drugie 10 %	20	5,5	5,0	20 0 9,6 8,2
Trzecie 10 %	30	6,5	6,2	30 0 16,1 14,4
Czwarte 10%	40	7,5	7,2	40 0 23,6 21,6
Piąte 10 %	50	8,4	8,3	50 0 32,0 29,9
Szóste 10%	60	9,5	9,5	60 0 41,5 39,4
Siódme 10 %	70	10,7	11.0	70 0 52,2 50,4
Ósme 10 %	80	12,2	12,8	80 0 64,4 63,2
Dziewiąte 10 %	90	14,4	15,2	90 0 78,8 78,4
Najwyższe 10 %	100	21,2	21,6	100 100 100 100

Gdyby dochody były rozłożone równomiernie, wówczas każde 20% społeczeństwa) otrzymywałoby dokładnie 20% wytworzonego dochodu globalnego. Jest to całkowita równość w podziale dochodów.

Drugim skrajnym przypadkiem jest sytuacja, w której tylko jedna osoba (grupa) otrzymuje cały wytworzony dochód; jest to całkowita nierówność w podziale dochodów Pomiędzy tymi skrajnymi przypadkami znajduje się rzeczywisty podział dochodu w społeczeństwie. W rzeczywistości skrajne przypadki nie występują Dowodzą tego dane zawarte w tabeli poniżej

Przestawiony w tabeli rzeczywisty rozkład dochodu możemy przedstawić w postaci linii ciągłej. Aby ją wykreślić na osi poziomej układu współrzędnych odkładamy odsetek wszystkich gospodarstw domowych w kolejności od najuboższych do najbogatszych, natomiast na osi pionowej odsetek przypadających na nie dochodów do dyspozycji.

%dochodu Rys Krzywa Lorenza

100%

75%

50%

25%

45 ) % gospodarstw domowych

50 60 90 100%

Biegnąca z początku układu współrzędnych pod kątem 45 stopni linia zielona ilustruje doskonałą równość rozkładu dochodu. Na linii tej procentowy udział ludności dochodach odpowiada idealnej strukturze dochodów. Leżące na tej linii punkty przedstawiają sytuację, w której 10 % ludności otrzymuje 10% dochodu, 20% ludności otrzymuje 20% dochodu i tak dalej. Wraz z przesuwaniem się do góry po krzywej doskonałej równości udział ludności w dochodach społeczeństwa ogółem wzrasta w jednakowym tempie

Wychodząca z początku układu linia pionowa ilustruje całkowitą nierówność podziału dochodu w społeczeństwie Pokazuje ona sytuację, w której 100% dochodu przypada niewielkiemu ułamkowi wszystkich gospodarstw domowych. Obydwie te krzywe ilustrują zatem sytuację, która w praktyce nie występują

Pomiędzy tymi dwoma skrajnymi przypadkami: absolutnej równości i całkowitej nierówności dochodów występuje rzeczywisty stan rzeczy z nierównomiernym rozkładem dochodów Przedstawia go linia czerwona/ niebieska zwana krzywą Lorenza.

Nasza krzywa zaczyna się ona w początku układu współrzędnych, gdzie 0 % gospodarstw domowych osiąga 0 % całkowitego dochodu do dyspozycji a kończy się w prawym, górnym rogu diagramu, gdzie 100 % gospodarstw domowych otrzymuje w sumie 100% tego dochodu. Punktu na krzywej pokazują, jaka część wszystkich dochodów przypada danemu odsetkowi gospodarstw domowych Kształt krzywej Lorenza wskazuje na stopień nierówności. Im bardziej jest ona wypukła, tym dochody są bardziej zróżnicowane..

Krzywa Lorenza znajduje dość szerokie zastosowanie, gdyż pozwala zilustrować zróżnicowanie dochodów (majątku) w określonej grupie społecznej w skali całego kraju a nawet w skali międzynarodowej. Pozwala ona również określić rozkładu dochodów wewnątrz różnych grup społeczeństwa oraz dokonywanie porównań w czasie. Jest do tego przydatnym narzędziem do analizowania skutków redystrybucji podatkowej.

Współczynnik Gianiego

Innym narzędziem pomiaru nierówności miarą nierówności w społeczeństwie jest pole pomiędzy linią doskonałej równości i krzywą, a dokładniej jego udział w całości obszaru pod linią doskonałej równości. Stosunek to nazywany jest współczynnikiem Gianiego.

Dla doskonałej równości przyjmuje on wartość 0, natomiast w sytuacji doskonałej nierówności jego wartość wynosi 1 Jego wartość może być w różnych krajach i w różnych okresach różna. I tak w USA po spadku w latach 1950-1970 z 0,37 do poziomu 0,31 wzrósł on w okresie 1970 -1970 do poziomu ca 0,4 (Zob. B. Czarny Podstawy .. cyt wyd s. 312.)

Wskaźniki statystyczne

Analizowana zmienna ekonomiczna może być wyrażona w wartościach absolutnych bądź względnych. Wartości absolutne są wyrażone w konkretnych jednostkach miary np. w kilogramach, litrach, sztukach, złotówkach i bezpośrednio informują o poziomie (rozmiarach) zmiennej. Litry i kilogramy są nieporównywalne Litr mleka jest nieporównywalny z litrem benzyny Nawet jednak, gdy mamy do czynienia a wielkościami jednorodnymi porównanie wielkości wyrażonych w liczbach absolutnych nie pozwala wyciągać wniosków, co do względnej wartości obserwowanych zmian.

Wartości względne informują o stosunku, w jakim jedna wartość absolutna ma się do drugiej Wielkości stosunkowe określane są najczęściej mianem indeksów lub wskaźników. Statystyczny wskaźnik, oznaka, cecha przedmiotu lub zjawiska połączona z pewną inną jego cechą takim stałym związkiem, że wystąpienie jej pozwala statystycznie (bezwyjątkowo) stwierdzić obecność lub przewidzieć zaistnienie tej innej cechy.

W statystyce rozróżnia się trzy zasadnicze wskaźniki: natężenia, struktury, dynamiki.

Przez pojęcie wskaźnik natężenia rozumiemy stosunek dwóch różnych wielkości pozostających w pewnym związku logicznym, np. stosunek liczby ludności jakiegoś kraju do wielkości jego terytorium. Tego typu wskaźnikiem jest gęstość zaludnienia

Gdy badanie polega na porównaniu części badanej zbiorowości z całą zbiorowością, posługujemy się wskaźnikami struktury, które określają, jaką część całości stanowią wyróżnione elementy.

Wskaźnik dynamiki to stosunek wartości zmiennej zależnej w okresie badanym jej od wartości w okresie podstawowym. Jest to liczba względna charakteryzująca zmiany poziomu zjawiska zachodzące w czasie.

Wśród indeksów dynamiki rozróżnia się indeksy indywidualne (proste), oparte na zmianach jednej wielkości, oraz związane z obliczeniami dotyczącymi całej zbiorowości oraz indeksy zespołowe (agregatowe), oparte na zmianach zespołu wielu wielkości, związane z obliczeniami dotyczącymi zbiorowości cząstkowych.

Wskaźniki struktury

Porównując zmiany w czasie badanej kategorii ekonomicznej musimy wystrzegać się błędnej interpretacji posiadanych danych i odróżniać wielkości absolutne od względnych (procentowych). Np. wzrost liczby telewidzów oglądających programy danej stacji telewizyjnej nie musi oznaczać, że kanał ten powiększył swój udział w liczbie telewidzów oglądających programy emitowane przez wszystkie kanały. O tym informują nas wielkości względne Dla lepszego zrozumienia tego problemu posłużymy się hipotetycznym przykładem bezrobocia wśród mężczyzn i kobiet.

Załóżmy, że w wyjściowym roku 1990 w Europejskiej Unii Gospodarczej bez pracy pozostawało 20 mln kobiet i 30 mln mężczyzn.

Wartości absolutne w roku1995 Wartości względne w roku 2000

20 mln kobiet 20:50=0,4 = 40 %

30 mln mężczyzn 30:50=0,6 = 60 %

--------------------- ---------

Razem 50 mln osób 100 %

W roku 2000 bez pracy pozostawało już 27 mln kobiet i 33 mln mężczyzn

Wartości absolutne w roku 2000 Wartości względne w roku 2000

27 mln kobiet 27:60= 0,45= 45 %

33 mln mężczyzn 33:60= 0,55= 55 %

---------------------- --------

Razem 60 mln osób 100 %

W wielkościach absolutnych liczba bezrobotnych kobiet wzrosła w interesującym nas okresie o 7 mln, jednocześnie ich udział w liczbie bezrobotnych zwiększył się z 40 do 45%. Natomiast liczba bezrobotnych mężczyzn wprawdzie wzrosła o 3 mln osób, lecz ich udział w łącznej liczbie bezrobotnych zmniejszył się z 60 do 55 %,a więc spadł o 5 %.Czym można wytłumaczyć spadek udziałów mężczyzn i wzrost udziału kobiet w sytuacji, gdy obie wielkości rosły jednocześnie? Zrozumiemy to,gdy zapoznamy się pojęciem stopy (lub tempa) wzrostu.

Stopa wzrostu

Jeżeli badana zmienna ekonomiczna przyjmowała w różnym czasie odmienne wartości, to można obliczyć jej ( dodatnią lub ujemną) stopę wzrostu.

Stopa wzrostu to wyrażony w procentach stosunek przyrostu zmiennej do poziomu wyjściowego tej zmienne rozpatrywany w przedziale dwóch punktów czasowych. Matematycznie można to ująć następująco:

x₂ - x₁

Stopa wzrostu = ----------- *100%

x₁

gdzie: x₂ - wartość zmiennej w okresie końcowym

x₁ - wartość zmiennej w okresie początkowym

Wróćmy na moment do naszego przykładu z bezrobociem wśród kobiet i mężczyzn. Łatwo możemy obliczyć, że gdy łączne bezrobocie wzrosło o 60-50=10; to jego tempo wzrostu ogółem wyniosło 10:50*100%=25%. W tym samym czasie tempo wzrostu bezrobocia wśród mężczyzn wynosiło (33-30):30*100%=10%, zaś tempo wzrostu bezrobotnych kobiet wyniosło odpowiednio (27-20):20*100%=35% .

Jak z tego wynika bezrobocie wśród kobiet rosło szybciej niż mężczyzn ,dlatego też ich udział w całości bezrobocia powiększał się. Z kolei bezrobocie mężczyzn rosło wolniej, dlatego ich udział malał.

Gdyby bezrobocie mężczyzn i kobiet rosło w jednakowym tempie np. 25% oba udziały pozostałyby niezmienione.

Stopa wzrostu a zmiany stopy wzrostu

Ujętą w procentach stopę wzrostu lub spadku łatwo pomylić ze zmianami wyrażonymi w punktach procentowych. Pomyślmy o wzroście ceny o 1% i porównajmy go ze wzrostem tempa wzrostu ceny o 1 punkt procentowy.

Otóż wzrost o 1 punkt procentowy nie oznacza stopy zmiany, lecz zmianę stopy wzrostu np. z 5% do 6% (jednak równie dobrze może chodzić o zmianę z 10 % do 11% czy z 6 do 5%.

W ekonomii posługujemy się bardzo często stopę wzrostu przy analizie dynamiki takich zmiennych jak:, inflacja, konsumpcja, oszczędności, inwestycji, czy produkcja

Dla przykładu rozpatrzmy produkcję przedsiębiorstwa, której ilość mierzona w sztukach zmieniła się następująco w ciągu kolejnych 4 lat :

Rok	1995	1996	1997	1998
Produkcja	1578	2473	3144	3998

Z zamieszczonej powyżej tabeli wynika jednoznacznie, że produkcja firmy wzrastała każdego roku, lecz ocena rozmiarów tego wzrostu w stosunku do poziomu produkcji z poprzedniego roku nie jest taka prosta. Im więcej danych porównujemy ze sobą tym trudniej zorientować się o sile tych zmian. Jeżeli natomiast obliczymy stopy wzrostu produkcji w badanych okresach, to łatwo nam będzie ocenić rozmiary względnych zmian i porównać je ze sobą w czasie:

Rok	1995	1996	1997	1998
Stopa wzrostu	-	56,7%	27,1%	27,1%

W celu zilustrowania korzyści, jaka wynikła z wykorzystania stopy wzrostu rozpatrzmy inny przykład. Załóżmy, że chcemy porównać zmiany produkcji zboża w różnych krajach. Zestawienie absolutnych ilości wzrostu produkcji ma ograniczone znaczenie. Ten sam przyrost produkcji, wynoszący 10 mln ton w dwóch krajach A i B, ma różne znaczenie wobec różnych wielkości początkowej w obu krajach.

Jeżeli produkcja w kraju A wynosiła początkowo 100 mln. a w kraju B 1 000 mln to wysiłek produkcyjny obu krajów dla osiągnięcia przyrostu 10 mln ton nie jest identyczny. Dopiero informacji o stopach wzrostu pozwala ocenić i silę się zmiany produkcji z każdym kraju. Stopa wzrostu wyniosła w kraju A=10%, a w kraju B=1%, czyli była 10 - krotnie niższa niż w A.

Istnieją inne metody obliczania stopy wzrostu danej wielkości. Można ją również obliczyć wykorzystując do tego indeksy dynamiki. Oblicza się je zwykle w procentach w stosunku do wielkości danego zjawiska w okresie przyjętym za podstawowy.

Wskaźniki dynamiki

Są to liczby względne przedstawiające stosunek poziomu zjawiska w okresie badanym do poziomu zjawiska w okresie przyjętym za podstawowy przemnożymy przez 100.W praktyce wartość okresu przyjętego za podstawę czyli bazowego jest kwestią naszego wyboru. . Jeśli z jakiś powodów zmienimy okres bazowy zmienią się również wartości obliczanych indeksów

Klasyfikacja indeksów dynamiki

W praktyce stosowane dwa rodzaje wskaźników dynamiki są to: indeksy indywidualne ( proste) porównujące wartości jednej zmiennej w stosunku do sytuacji wyjściowej (bazowej) oraz indeksy zespołowe (agregatowe) oparte na zmianach zespołu wielu wielkości, związane z obliczeniami dotyczącymi zbiorowości cząstkowych. Ponadto indeksy dzielimy na jednopodstawowe i łańcuchowe

Indeksy indywidualne (proste)

Dysponując wartościami analizowanej zmiennej w różnych okresach czasu, możemy tabelarycznie przedstawić szereg czasowy, opisujący np. ogólne spożycie piwa a hektolitrach w hipotetycznym kraju:

Lata	1955	1960	1965	1970
Spożycie piwa w hektolitrach	262,7	275,8	368,8	469,1

Dla niewprawnego analityka dane te mogą być mało czytelne. Nie uwidaczniają one ani wyraźnie przyrostów absolutnych ani względnych (procentowych) zmian spożywanych ilości w kolejnych okresach. Usuniemy te niedogodności, gdy dla kolejnych lat obliczymy indeksy dynamiki, czyli wskaźniki opisujące zmiany określonej wielkości w czasie. Obliczamy je według ogólnej formuły zapisanej wzorem poniżej:

Wartość zmiennej w badanym roku

----------------------------------------------- * 100

Wartość zmiennej w roku bazowym

Indeksy dynamiki występują w dwóch postaciach. Jeśli dane z kolejnych okresów porównujemy do tej samej wielkości bazowej (stałej podstawy) posługujemy się tzw. indeksem jedno podstawowymi. Indeks dla okresu bazowego wynosi 100. Jeżeli natomiast porównujemy ze sobą danymi z każdego kolejnego okresu, kiedy indeks dla rok przedniego wynosi 100, to posługujemy się tzw. indeksem łańcuchowych

W pierwszym przypadku otrzymaną wartość wskaźnika odnosimy do jednego okresu bazowego (niekoniecznie musi być to okres poprzedni). W drugim zaś każdą kolejną wielkość porównujemy z wielkością uzyskaną w poprzednim okresie.

Indeksy o stałej podstawie ( jednopodstawowe)

Biorąc za punkt wyjścia dane dotyczące konsumpcji piwa obliczmy indeksy jednopodstawowe dla kolejnych lat. Jako rok bazowy przyjmujemy rok 1955 Oto otrzymane wyniki

- dla roku 1955 indeks wynosi 100 (262,7/262,7) * 100 = 100

- dla roku 1960 indeks wynosi 105 (275,8/ 262,7) *100 = 105,0

- dla roku 1965 indeks wynosi 140,4 (368,8 / 262,7) *100 = 140,4

- dla roku 1970 indeks wynosi 178,6 (469,1/ 262,7) *100 = 178,6

Wszystkie obliczone powyżej indeksy możemy zgrupować w poniższej tabeli

Rok	1955	1960	1965	1970
Spożycie ogółem - rok bazowy 1955	100,0	105,0	140,4	178,6

Nie operując konkretnymi wartościami spożycia piwa w poszczególnych latach, możemy dokonać analizy jej zmian na przestrzeni 4 kolejnych lat wykorzystując jedynie wskaźniki rokiem przyjętym jako bazowy jest rok 1955; w stosunku do niego odnosić będziemy zmiany konsumpcji zachodzące w kolejnych latach

Indeksy dynamiki a tempo wzrostu

Dysponując indeksem zmiany danej wielkości w pewnym okresie, możemy łatwo obliczyć liczone w procentach tempo zmian. Wielkość tę otrzymujemy przez odjęciu od uzyskanego wskaźnika wartości wskaźnika bazowego (100). Oznacza to, że zmiana wartości absolutnej wskaźnika obrazuje względną (procentową) zmianę badanej zmiennej.

Jeżeli obliczony wskaźnik wynosi np. 90 oznacza to, że wartość zmiennej spadła o 10 % w stosunku do jej wartości z roku bazowego (90 - 100 = - 10% ).

Jeżeli zaś obliczony wskaźnik wynosi np. 120 oznacza to, że wartość zmiennej wzrosła o 20 % w stosunku do okresu bazowego (120 - 100 = + 20%)

A teraz, odwołując się do danych w tabeli, obliczmy procentowe zmiany konsumpcji piwa w badanym okresie w stosunku do okresu bazowego:

- w roku1960 spożycie wzrosło o 5% w porównaniu z 1955 ( 105 - 100 = 5%)

- w latach 1955 - 1965 wzrosło o 40,4% (140,4 - 100 = 40,4 %_)

- w roku 1970 w porównaniu do 1959 wzrosła o 78,6 % r ( 178,6 - 100 = 78,6%)

Rok	1955	1960	1965	1970
Spożycie ogółem - rok bazowy 1960	267,5; 275,8* 100=95,2	100	368,8;275,8*100-133,7	469,1;275,8*100=170,0

Oczywiście przyjmowany do badania rok bazowy może być dowolnym rokiem; wybór uzależniony jest od celu prowadzonej analizy. Załóżmy, że obecnie interesują nas zmiany konsumpcji piwa w stosunku do roku 1960 i to on będzie przyjęty za podstawę obliczeń (100). Sposób przeliczania jest bardzo prosty - obecnie stałym mianownikiem jest wartość spożycia z roku 1960 zaś licznik tworzą kolejne wartości konsumpcji z lat 1955, 1960 i 1970. Nasza tabela będzie więc przedstawiała się następująco:

Powyższe przekształcenia mogą być przeprowadzone także na wartościach samych indeksów, bez wykorzystania absolutnych wartości wydatków gospodarstw domowych.

Lata	1955 = 100	1960 = 100
1959	100	95,2, = ( 100/ 105 ) * 100
1960	105	100
1965	140,4	133,7 = ( 140,4 / 105 ) * 100
1970	178,6	170,0 = ( 178,6 / 105 ) * 100

W powyższym przypadku kolejne wartości wskaźników ilustrują zmiany wartości wydatków konsumpcyjnych w stosunku do stałej podstawy - roku przyjętego za bazowy (w naszym przykładzie najpierw roku 1959 a potem rok 1960). Nie uwidaczniają one jednak zmian interesującej nas zmiennej z roku na rok. Do tego celu służą indeksy łańcuchowe

Indeksy łańcuchowe

Indeksy łańcuchowe są wskaźnikami ilustrującymi zmiany interesującej nas wartości odnoszone do poprzedniego okresu. W takiej sytuacji każdy poprzedni rok (miesiąc, dzień itp.) przyjmujemy za bazowy - zmiennym będzie zatem zarówno licznik, jak i mianownik wzoru 1.1. Przeanalizujmy to na naszym hipotetycznym przykładzie:

Rok	1955	1960	1965	1970
Spożycie w hektolitrach	262,7	275,8	368,8	469,1

A teraz obliczmy indeksy łańcuchowe

Rok	1955	1960	1965	1970
Spożycie ogółem w cenach stałych rok poprzedni = 100	100	105 = 275,8 / 262,7 ) *100	133,7 = ( 368,8 /275,8 ) *100	127,1=(469,1/368,8) *100

Gdy od indeksu łańcuchowego odejmiemy 100 otrzymamy tempo wzrostu badanej wielkości w stosunku do okresu poprzedniego

Indeksy łańcuchowe a jednopodstawowe

Przekształcenie indeksów łańcuchowych we wskaźniki o stałej podstawie jest bardzo proste i następuje według zasady:

Przeanalizujmy to na naszym przykładzie:

Na skutek zaokrągleń, wskaźniki dynamiki o podstawie 1955 = 100 obliczone w powyższych tabelach dwiema metodami często przyjmują nieco odmienne wartości (np. dla roku 1970 o 0,2).

Lata	Spożycie ( rok poprzedni = 100)	Spożycie ( rok 1955 = 100 )
1955	100,0	100,0
1960	105,0	105,0 = ( 105 *100 ) / 100
1965	133,7	140,4 = ( 133,7 * 105 ) / 100
1970	127,1	178,4 = ( 127,1 * 140,4 ) / 100

Proste indeksy dynamiki są bardzo praktycznymi w narzędziami w ręku ekonomisty Po pierwsze umożliwiają one ustalenie i porównanie tempa wzrostu badanych wielkości w kolejnych okresach. Po drugie, ponieważ są to wartości względne, pozwalają porównywać ze sobą wielkości wyrażonych w różnych nieporównywalnych ze sobą jednostkach fizycznych Jednakże są one nieprzydatne, gdy mamy do czynienia z agregatami.

Indeksy zespołowe (agregatowe)

W tym przypadku agregatów stosuje się indeksy agregatowe. Ponieważ ich wartość zależy między innymi od struktury agregatu, są to najczęściej indeksy ważone. Wagami są udziały poszczególnych części składowych w całości tworzonego przez nie agregatu.

Agregacja wielkości ekonomicznych:

Istnienie ogromnej ilości dóbr i usług powoduje, że w życiu gospodarczym rzadko posługujemy się pojedynczymi wielkościami naturalnymi, natomiast bardzo często odwołujemy się do miar syntetycznych, czyli agregatów. Agregacja to ogólny termin określający łączenie się mniejszych cząstek w większe. Agregaty to połączone w jedną całość za pomocą jednej wspólnej jednostki miary zbiory składające się przynajmniej dwóch niejednorodnych elementów.

W ekonomii najczęściej stosowanym narzędziem agregacji są istniejące na danym obszarze ceny dóbr i usług Agregacyjna funkcja ceny umożliwia mierzenie nakładów i efektów danego przedsięwzięcia, co tworzy warunki do przeprowadzenia rachunku ekonomicznego. Dzięki temu zamiast ogromnej ilości mierników wyrażonych w wielkościach fizycznych można posługiwać się niewielką ilością syntetycznych mierników wartościowych Nie ma jednak róży bez kolców. Jak się niebawem przekonamy stosowanie cen i mierników wartościowych stwarza ogromne trudności metodologiczne?

Jaka obliczamy wartość agregatów?

W badaniach statystycznych posługujemy się agregatami o zmiennej zawartości i strukturze np. Produkt Krajowy Brutto i stałej zawartości i strukturze czyli tzw. koszykami

Zacznijmy od agregatów o zmiennej wielkości i strukturze. Najprościej jest oprzeć się na przykładzie liczbowym Dotyczy on wartości produkcji sprzedanej przez firmę BETA w roku 1990 oraz w roku 1995.

Przyjmijmy, że przedsiębiorstwo nasze wytwarza dwa nie dodawalne do siebie produkty: zeszyty i segregatory. Aby ustalić łączną wielkość produkcji, musimy sprowadzić je do wspólnej podstawy wartościowej. W tym celu musimy fizyczne ilości zeszytów i segregatorów przemnożyć przez ich ceny rynkowe i uzyskane wartości obu produktów do siebie dodać. Otrzymany w ten sposób agregat nazwiemy wartością produkcji sprzedanej Obliczmy ja posługując się danymi zawartymi w tabeli poniżej.

	Cena sprzedaży w 1990 r	Cena sprzedaży w 1991 r	Sprzedane ilości w 1990r	Sprzedane ilości w 1991r	Wartość sprzedaży w 1990 r	Wartość sprzedaży w 1991r
Zeszyty	5	7	100	100	5* 100= 500	7*100= 700
Segregatory	8	10	200	160	8* 200 = 1600	10*160= 1600
RAZEM					2100	2300

Z przeprowadzonych na podstawie danych w tabeli obliczeń wynika, że licząc w bieżących cenach rynkowych w roku 1990 firma sprzedała produkcję wartości 2100 zł. Natomiast w roku 1991 wartość produkcji sprzedanej wyniosła 2300 zł

Indeksy zespołowe (agregatowe)

Znając wartość agregatów w obu badanych okresach możemy bez trudu obliczyć indeks zagregowanej wartości produkcji. Wystarczy porównać ze sobą wartości w obu okresach i uzyskany wynik pomnożyć przez sto

2300zł:2100zl*100=109,5

Czy jednak na podstawie tego wyniku możemy wnioskować, że produkcja firmy w wyrażeniu fizycznym wzrosła o:

109,5- 100=9,5%

Otóż nic bardziej błędnego! Z tabeli wynika, że produkcja i sprzedaż zeszytów pozostała na tym samym poziomie prosty indeks dla zeszytów wynosi zatem dla obu okresów 100: 100*100=100, zatem tempo wzrostu fizycznej wielkości to 100- 100=0%

Z kolei produkcja i sprzedaż segregatorów spadła z 200 do 160. Indeks prosty dla fizycznych wielkość segregatorów wynosi 160:200*100=80, zatem produkcja segregatorów spadła w badanym okresie o 80-100=-20%

Skąd w takim razie wziął się równy 109,5 indeks zagregowanej wartości i dodatnie 9,5% tempo wzrostu produkcji?

W naszym przypadku jedynym sprawcą wzrostu wartości sprzedaży jest wzrost użytych do agregacji cen,

Cena zeszytów wzrosła 7zł-5 zł=2zł. Prosty indeks cen zeszytów wyniósł zatem w tym czasie

7zł:5zł *100=140

co oznacza , że zeszyty zdrożały w tym czasie o 140-100= 40%

Cena segregatorów wzrosła 10zł- 8zł=2zł zatem prosty indeks cen dla segregatorów w wyniósł badanym okresie

10zl :8zł *100=125

co oznacza że cena segregatorów wzrosła o 125- 100= 5%.

Z przedstawionych w przykładzie danych widać jednak wyraźnie, że zmiany absolutne wartości nominalnej produkcji i zmiany względne wartości agregatu o 109,5-100=9,5% wynikały tylko i wyłącznie że wzrosty poziomu użytych do obliczeń cen sprzedaży..

Posługując się wyłącznie wartościowym miernikiem produkcji w postaci nominalnej, możemy dojść do błędnego wniosku, że produkcja przedsiębiorstwo BETA w badanym okresie wzrosła.

Od czego zależy zmiana wartości agregatu

Nasze dane dotyczą agregatu wyrażonego w formie wartościowej. Zmieniają się one pod wpływem przynajmniej trzech czynników:

- zmian fizycznych rozmiarów (zmian ich wolumenu)

- zmiany poziomu ceny, które powiększają lub pomniejsza ją wyłącznie ich wartość pieniężną a nie fizyczną

- osobny problem to zmiany struktury agregatu

Analizują, zatem dokonujące się w czasie zmiany wartości agregatu musimy brać pod uwagę wpływ, jaki wywiera na ich wartość zmiany poziomu agregujących je cen. Aby zatem móc określić faktyczną zmianę wyrażonej wartościowo kategorii musimy odróżnić od siebie wielkości nominalne i realne.

Wielkości nominalne to wartości wyrażone w cenach bieżących, czyli obecnie obowiązujących na rynku). Przedstawiają one zatem wartość zmiennej ekonomicznej, której poziom zmierzono został pieniądzem o sile nabywczej z okresu, do którego się ona odnosi.

Wielkości realne to wartości wyrażone w cenach stałych a więc w cenach z interesującego nas okresu minionego, który uznamy za bazowy. Inaczej mówiąc przedstawiają one wartości zmiennej ekonomicznej, mierzonej pieniądzem o sile nabywczej z jednego okresu, przyjętego przez nas za bazowy.

Produkcja w wyrażeniu realnym

Ponieważ w naszym przykładzie rosnące ceny sztucznie zawyżają wzrost wartości produkcji postaramy się ten wpływ wyeliminować. Dzięki temu staną się one porównywalne

W tym celu obliczamy wartość agregatów w obu analizowanych latach w jednakowych cenach albo z roku 1990 albo z roku 1991

	Cena sprzedaży w 1990 r	Cena sprzedaży w 1991 r	Sprzedane ilości w 1990r	Sprzedane ilości w 1991r	Wartość sprzedaży w 1990 r	Wartość sprzedaży w 1991r
Zeszyty	5	7	100	100	500	500
Segregatory	8	10	200	160	1600	1280
RAZEM	-	-	-	-	2100	1780

Przyjmijmy, że okresem bazowym jest rok 1990. Przeliczona po tych cenach wartość produkcji w roku 1991 wynosi

Wartość produkcja zeszytów w 1991 w cenach stałych 100 sztuk *5 zł = 500 zł

Wartość produkcja segregatorów w 1991 w cenach stałych 160 sztuk * 8 zł = 1 280 zł

Razem 1 780 zł

Z powyższego wynika, że łączna produkcja w roku 1991 wyrażona w porównywalnych cenach z roku 1990 wynosiła 1780 zł a zatem w rzeczywistości (realnie) nie wzrosła, lecz spadła o 1780zł - 2100zł =- 320zl .

Aby obliczyć wskaźnik produkcji realnej musimy porównać ze sobą produkcje realną w obu badanych okresach. Wynosi on

1780: 2100 *100=84,76

Procentowy spadek realnej produkcji możemy obliczyć jako 84,7-100= -15,2% Do identycznego wyniku dojedziemy porównując przyrost produkcji realnej z jej wielkością początkowa -320zł: 2100zł *100% = -15,2%.

Względne zmiany cen mogą zniekształcić obraz

Dla celów naszej analizy wybraliśmy ceny z roku 1990 zobaczymy, czy identyczne wyniki uzyskam, gdy obliczenia przeprowadzimy w cenach z roku 1991

	Cena sprzedaży w 1990 r	Cena sprzedaży w 1991 r	Sprzedane ilości w 1990r	Sprzedane ilości w 1991r	Wartość sprzedaży w 1990 r	Wartość sprzedaży w 1991r
Zeszyty	5	7	100	100	700	700
Segregatory	8	10	200	160	2000	1600
RAZEM					2700	2300

Produkcja zeszytów w 1991 w cenach stałych 100 sztuk *7 zł = 700 zł

Produkcja segregatorów w 1991 w cenach stałych 160 sztuk * 10 zł = 1 600 zł

Razem 2 300 zł

Z powyższego wynika, że łączna produkcja w roku 1991 wyrażona w porównywalnych cenach z roku 1991 wynosiła 2 300 zł a zatem w rzeczywistości(realnie) nie wzrosła, lecz spadła o 2400- 2700 =-400zł.

Procentowy spadek realnej produkcji możemy obliczyć porównując przyrost produkcji realnej z jej wielkością początkowa -400: 2 700 *100% = -14,8%.

Aby obliczyć wskaźnik produkcji realnej musimy porównać ze sobą produkcje realną w obu badanych okresach a uzyskany wynik pomnożyć przez 100. Wynosi on

2 300: 2 700*100= 85,2

Różnica wyników jest spowodowana tym, że użyte dla obliczeń ceny wartości agregatu ceny zmieniły się w różnym tempie. Posługując się danymi z powyższego przykładu możemy bez trudu obliczyć proste indeksy cen dla każdego ze sprzedawanych przez firmę wyrobów. Indeks cen zeszytów wynosi 7:5*100=140 natomiast indeks cen segregatorów wyniósł odpowiednio 10:8*100=125. Wynika z tego ze w okresie 1990-1991 oba wyroby nie drożały w jednakowym tempie Zeszyty zdrożały o 40 % zaś segregatory mniej bo tylko o 25 %.

Indeksy zmian przeciętnego poziomu cen

W statystyce często operuje się pojęciem średniego tempa wzrostu. Czy aby je ustalić wystarczy obliczyć średnią arytmetyczną, to znaczy dodać do siebie tempa cząstkowe i podzielić je przez dwa. Czy średnie tempo wzrostu obu cen wyniosło (40+25):2= 32,5 % ?

Otóż nie, ale istnieją bardziej subtelne i precyzyjne metody, które uwzględniają nie tylko zmiany cen i ilości, ale również zmiany udziału poszczególnych produktów w tworzeniu agregatu W efekcie otrzymujemy wskaźnik zmiany przeciętnego poziomu cen w danym okresie.

Indeksy cen ważone

Wartość fizycznego wolumen w danym roku możemy obliczyć oddzielnie w cenach bieżących (wartość nominalna) i w cenach stałych (wartość realna). Jeśli teraz nominalną wartość w cenach bieżących podzielimy przez realną wartość w cenach stałych i uzyskany wynik pomnożymy przez 100, to wyniku tych operacji otrzymamy indeks zmian przeciętnego poziomu cen. Jego wartość informuje nas w jakim stopniu zmiany wartości agregaty spowodowany został tylko i wyłącznie zmianami cen. Jest to zatem wskaźnik przeciętnego wzrostu cen. Syntetycznie zapisujemy to jak poniżej

Wartość nominalna agregatu

--------------------------------------- * 100

Wartość realna agregatu

W naszym przykładzie liczbowym nominalna wartość produkcji zeszytów i segregatorów w roku 1991 wynosiła 2300 zł, natomiast realna wartość produkcji w tym okresie wyniosła tylko 1780 zł Wstawiając te dane do wzoru powyżej obliczamy wskaźnik przeciętnego wzrostu cen, w badanym okresie wynosił.

2300:1780 *100=129,2

Aby obliczyć średnie tempo wzrostu cen od indeksu odejmujemy 100 W naszym przykładzie wynosi ono 129,2-100=29,2 %, a nie jak obliczyliśmy na podstawi średniej arytmetycznej ( 40+25):2= 35 %

W zależności od rodzaju stosowanych agregatów zmiany ogólnego poziomu cen mierzymy albo przy pomoce delatorów, w których zmieniają się ilości i ceny albo przy pomocy koszyków , gdzie ilości pozostają stałe

Deflatory

Gdyby analizowana firma sprzedawała trzy produkty nasz wskaźnik obejmowałby trzy ceny, gdy cztery to uwzględnilibyśmy cztery ceny itd. Im więcej produktów i cen uwzględniamy w naszym wskaźniku, tym dokładniej tak obliczany wskaźnik informuje nas o zmianie ogólnego poziomu cen.

Można wyobrazić sobie agregat, w którym uwzględnia się wartość wszystkich wytwarzane w gospodarce produktów. Wskaźnik zmian nominalnej wartości tego agregatu informowałby o zmianach poziomu cen wszystkich sprzedawanych dóbr i usług a zatem dysponowalibyśmy wskaźnikiem zmian przeciętnego poziomu cen w skali całej gospodarki.

Tego typu wskaźnikami będziemy posługiwać się w analizach makroekonomicznych gdzie przedmiotem analizy są duże służące do badania i określania stanu aktywności gospodarczej całej gospodarki agregaty Takim bardzo pojemnym agregatem z zmiennej strukturze jest Produkt Globalny (PG), liczony jako sumą wartości wszystkich wytworzonych w danym okresie dóbr i usług

Jeżeli porównamy ze sobą produkt globalny nominalny, czyli liczonym w cenach bieżących (licznik) z tym produktem globalnym realnym, czyli tym samym fizycznym produktem, ale liczonym w cenach stałych z okresu bazowego(mianownik), to w wyniku dzielenia otrzymamy najogólniejszy makroekonomiczny wskaźnik zmian poziomu cen zwany deflatorem produktu globalnego

n

Produkt globalny nominalny ΣQi*Ci1

i=1

Def PG= ------------------------------------*100= -------------*100

n

Produkt globalny realny ΣQi*Ci0

i=1

Gdzie:

Qi- ilości dóbr i usług

Ci0 -ceny w okresie bazowym

Ci1-ceny w okresie bieżącym

Trochę mniej pojemny jest Produkt Krajowy Brutto (PKB), który liczony jako suma wartości wszystkich wytworzonych na terenie danego kraju dóbr finalnych Do agregatu tego nie wlicza się dóbr pośrednich, to znaczy tych, które w badanym okresie zostały wytworzone, ale były poddane dalszemu przetwarzaniu a zatem zostały w badanym okresie całkowicie fizycznie zużyte do wytwarzania innych dóbr.

Jeżeli przy obliczaniu wskaźnika przeciętnego wzrostu cen posługujemy się agregatem Produktu Krajowego Brutto, wówczas uzyskujemy wskaźnik przeciętnego wzrost nazywamy deflatorem produktu krajowego brutto Wskaźnik ten cechuje mniejszy stopień szczegółowości

PKB nominalny ΣQfi*Ci1

Def PKB= -------------------------*100 =- -----------------*100

PKB realny ΣQfi*Ci0

Gdzie

Qi- ilości dóbr i usług finalnych

Ci0 -ceny w okresie bazowym

Ci1-ceny w okresie bieżącym

Podobne deflatory możemy obliczyć dla zagregowanej wartości konsumpcji inwestycji itp. Wymienione powyżej indeksy ograniczają swoje badania do określonego w nazwie rodzaju dóbr ( konsumpcyjnych, produkcyjnych i wszystkich dóbr finalnych).

Cechą charakterystyczną deflatorów jest duża ilość dóbr i usług wchodzących oraz zmienność ich udziałów w całości stanowiących podstawę ich obliczeń agregatów

Im więcej dóbr i usług obejmuje użyty do pomiaru agregat, tym dokładniej informuje o zmianie ogólnego poziomu cen. Jednakże im większy agregat tym obliczanie zmian ogólnego poziomu cen za pomocą wymaga więcej czasu pracy i pieniądz jest kosztowniejsze Dlatego w praktyce stosuje się inne mniej skomplikowane i bardziej rutynowe metody pomiaru Są one oparte na badaniu zmian wartości wybranych dóbr, które są zgrupowane w tzw. koszykach.

Wskaźniki cen oparte na koszykach

Zmiany ogólnego poziomu cen oblicza się również przy pomocy indeksów bazujących na stałych koszykach Najczęściej stosowane to indeks cen dóbr konsumpcyjnych ( ang consumer price index CPI), indeks cen hurtowych i indeks cen produkcyjnych

Wskaźnik cen detalicznych (WCD)

Indeksy cen dóbr konsumpcyjnych służy przede wszystkim do pomiaru zmian kosztów utrzymania są to a to zatem indeksy kosztów utrzymania (ang. cost of living index) Najważniejszy z nich jest wskaźnik cen detalicznych (WCD) Obliczamy go nie dla całego PKB a tylko dla opracowanego dla okresu bazowego stałego koszyka zawierającego reprezentatywne dla przyzwyczajeń i gustów społeczeństwa dobra i usługi Wchodzące w skład koszyka dobra ustalana Główny Urząd Statystyczny

Zmiany cen detalicznych w kolejnych latach powodują wzrost lub spadek wartości tego koszyka Indeks cen detalicznych dla danego okresu obliczamy, gdy podzielimy jego wartość z tego okresu przez wartość z okresu bazowego a uzyskany iloraz pomnożymy przez sto.

Wynik większy od stu informuje, że przeciętny poziom cen wzrósł (inflacja) mniejszy, że zmalał (deflacja). Gdy od wartości indeksu odejmiemy sto dowiemy się jaka była stopa czyli inaczej (tempo) inflacji (ang inflation rate) lub deflacji. Indeks ten jest narzędziem umożliwiającym mierzenie zmiany siły nabywczej pieniądza, zmian kosztów utrzymania, umożliwia również przeliczanie wartości nominalnych na realne i na odwrót Kształtowanie się tego wskaźnika może zatem stanowić podstawę dla podejmowania decyzji, co do zmiany (rewaloryzacji) płac i świadczeń społecznych

Poniższy oparty na danych z tabel przykład pokazuje w uproszczony sposób zasady obliczania tego wskaźnika w dla jakiegoś dowolnego okresu czasu

Konsumpcja całkowita	Wartość wydatków w roku I w zł	Wartość wydatków w roku II w zł	Indeks cen w I roku Rok I - bazowy	Proste indeks cen dla II roku
Kawa	10 kg*5zł/k g= 50 zł	10kg*5,5zł/kg= 55zł	100	(55:50)*100= 110
Chleb	30 kg*2,5zł/kg = 75 zł	30kg*2,5 zł /kg = 75zł	100	75:75*100= 100
Mięso	10 kg*12,5zł/kg 125 zł	10kg* 15 zł kg = 150zł	100	15:12,5*100= 120
Razem	250 zł	280zł

Załóżmy, że przeciętny konsument pan Kowalski cały swój dochód przeznacza na zakup tylko trzech dóbr konsumpcyjnych. W roku wyjściowym kupuje 10 kg kawy płacąc 5zł za kilogram, 30 kg chleba po 2,5 złotego i 10 kg mięsa po 12,5 zł za kilogram. Łatwo obliczyć, jego całkowite wydatki na poszczególne dobra w roku bazowym. Kawa kosztuje go 50 zł, chleb 75 zł a mięso 125 zł Łącznie wydaje, więc 250 zł.

Załóżmy, że w roku drugim płaci za te same ilości kawy 55 zł, chleba 75 zł, a mięsa 150 zł. Na podstawie posiadanych informacji możemy obecnie bez trudu zbudować tabelę, która pomoże nam obliczyć wskaźniki zmian cen poszczególnych towarów oraz wskaźnik wzrostu przeciętnego poziomu cen wszystkich kupowanych przez Kowalskiego dóbr.

Z dokonanych obliczeń wynika, że w ciągu dwóch kolejnych lat, cena kawy wzrosła o 10 %, ceny chleba pozostały bez zmian, zaś ceny mięsa wzrosły o 20 %.

Pytanie jednak brzmi, o ile procent w ciągu tego okresu zmieniła się wartość nabywanego koszyka konsumpcyjnego złożonego z trzech dóbr (kawy, chleba i mięsa)? Inaczej mówiąc, o ile procent wzrosły przeciętnie ceny wszystkich dóbr i usług konsumpcyjnych? Odpowiedź na to pytanie pozwoli nam ustalić, jak zmieniły się koszty utrzymania pana Kowalskiego? Do uzyskania właściwej odpowiedzi posłużymy się dwiema metodami.

Pierwsza z nich polega na obliczeniu procentowych zmiany wartości tego samego niezmienionego pod względem ilościowym koszyka zakupów Kowalskiego.

Koszt koszyka konsumpcyjnego w I roku wynosił: 50 zł+75 zł+125 zł = 250 zł. Natomiast koszt tego samego koszyka w II roku wynosił: 55 zł + 75 zł + 150 zł = 280 zł.

W takiej sytuacji indeks wzrostu kosztów utrzymania wynosi: ( 280 / 250) x 100 = 112, co oznacza wzrost jego wartości o 112-100=12 %.

Spożycie	Udział w całości wydatków	Wskaźniki wzrostu cen	Iloczyny wskaźników wzrostu cen i wagi	Indeksy cząstkowe
Kawa	50:250=0,2	110	110*0,2	22
Chleb	75:250=0,3	100	100*0,3	30
Mięso	125:250=0,5	120	120*0,5	60
RAZEM				112

Drugi sposób bazuje na wykorzystaniu znajomości wag poszczególnych produktów w całości wydatków Kowalskiego i indeksów zmian cen tych produktów . Chcąc przedstawić zmiany ogólnego poziomu cen konsumpcyjnych musimy objąć swoją analizą wszystkie nabywane przez konsumentów dobra i usługi. Należy pamiętać jednak, że wydatki na poszczególne towary mają różne znaczenie w budżecie poszczególnych rodzin.

Udziały wydatków na poszczególny produkt dla konsumenta w globalnych wydatkach gospodarstwa domowego przedstawiają ich ważność W naszym rachunku są to tzw. wagi. Łatwo obliczyć, że w roku bazowym na kawę wydawał on 20%, swoich dochodów, na chleb 30 %, zaś wydatki na wyroby mięsne stanowiły 50 %

Aby obliczyć średnie dla wszystkich dóbr tempo wzrostu cen, musimy od obliczonego jako średnia ważona indeksu kosztów utrzymania w drugim roku wynoszącego 112 odjąć wynoszący 100 indeks z roku pierwszego. Otrzymana różnica to nic innego tylko przeciętne tempo wzrostu cen w badanym okresie wszystkich branych pod uwagę dóbr

Wzrost cen kawy i mięsa nie wpłynęły jednakowo na sytuację pana Kowalskiego. Zmianę całkowitych kosztów utrzymania obliczymy w następujący sposób: wartość indeksu cen każdego z nabywanych dóbr mnożymy przez udział tego towaru w całkowitych wydatkach pana Kowalskiego, a otrzymane iloczyny dodajemy do siebie. Obliczany w ten sposób indeks kosztów utrzymania wynosi:

110 * 0,2 + 100 * 0,3 + 120 * 0,5 = 22 + 30 + 60 = 112

Z przeprowadzonych w ten sposób obliczeń wynika, że spowodowane wzrostem cen koszty utrzymania wzrosły o 112- 100= 12 %.

Wpływ zmiany wag na wartość indeksu

Wartość indeksu ważonego determinowana jest nie tylko zmianą wartości samych zmiennych (np. cen), ale także wagami. To one decydują o wartość wskaźników cząstkowych tworzących syntetyczny wskaźnik np. kosztów utrzymania. Gdy struktura konsumpcji i wydatków jest inna, inna będzie również wartość indeksu kosztów utrzymania.

Jeżeli w wydatkach pana Nowaka, kawa i chleb zajmują po 10% w całkowitych wydatkach, zaś pozostałe 80% przypada na zakupy mięsne, to jego wskaźnik kosztów utrzymania przyjmie wartość (110*0,1+100*0,1+120*0,8)=117. Koszty utrzymania mięsożernego Nowaka wzrosły bardziej niż Kowalskiego, bo aż 17%. Wynika z tego, że każdy z nas w zależności od indywidualnych gustów i upodobań kształtujących naszą konsumpcję w różny sposób odczuwa zmiany ogólnego poziomu cen

Deflator kontra wskaźnik kosztów utrzymania

Wydawać by się mogło, że wskaźnik cen detalicznych jest w stosunku do deflatora równoważną miarą zmian ogólnego poziomu cen Okazuje się, że obie metody nie prowadzą do identycznych wyników.

Po pierwsze, deflator obejmuje wszystkie dobra i usług finalne wyprodukowane w gospodarce w ciągu roku (czołgi, tramwaje, szynka, piwo), Pokazuje więc on nie tylko zmiany cen dóbr konsumpcyjnych, ale i inwestycyjnych oraz ceny towarów nabywanych przez rząd, wyłączając jednak dobra importowane. Stosując deflator posługujemy się zatem dużo szerszym agregatem , mamy wiec do czynienia z lepszy narzędziem pomiaru zmian ogólnego poziomu cen.

Z kolei przy obliczeniach wskaźnika cen detalicznych uwzględnia się tylko ceny niektórych dość arbitralnie wybranych dóbr i usług towar6w nabywanych wyłącznie przez konsumentów; pomija się zatem ceny dóbr nabywanych przez rząd (czołgi, tramwaje) i dóbr inwestycyjnych nabywanych przez firmy budynki maszyny surowce itp. Jednak, w przeciwieństwie do deflatora, w zmianach wartości WCD uwzględnione zostają zmiany cen dóbr importowanych, zakupywanych przez gospodarstwa domowe.

Po wtóre, techniki obliczania obu indeksów są różne. Indeks cen kon­sumenta bazuje na tzw. stałym koszyku dóbr bazowych. W każdym roku dobra wchodzące do tego koszyka są przemnażane przez ceny obowiązujące w danym roku. W ten sposób uzyskuje się informacje, ile wydano na ten sam koszyk w kolejnych latach. Przez porównanie z wydatkiem na ten koszyk w roku bazowym uzyskuje się informację o zmianach WCD Koszyk jest ten sam; zmianie u1egają ceny, a zatem przy tego rodzaju obliczeniach w zasadzie nie uwzględnia się wpływu zmian struktury zakupów na zmianę ogólnego poziomu cen.

Zmiany produktów reprezentantów ilości dóbr w koszyku, a co zatem i struktury koszyka są wprawdzie dokonywane, ale przeprowadzane są co kilka lat.

Inaczej sprawa wygląda przy deflatorze. Tutaj koszyk ulega co roku zmia­nie, a ceny są stałe (okresu bazowego). Deflator jest ściśle, zwią­zany z PKB, a ten wykazuje zawsze towary i usługi nabyte w bie­żącym, a nie bazowym roku. Stąd też towary konstytujące bieżący PKB to nowy koszyk dóbr przyjmowany do obliczeń. Przemnażany jest on przez ceny roku bieżącego (nominalny PKB) oraz ceny roku bazo­wego (realny PKB), a ten mówi, ile zaplaci1ibyśmy za tegoroczny PKB, gdyby obowiązywały ceny z roku bazowego). Zestawiając ze sobą te dwie wartości, otrzymujemy delator PKB. Obliczając ·deflator uwzględniamy, co roku inne wielkości fizyczne produkcji poszczególnych dóbr, a zatem uwzględniamy również wpływ zmiany jej struktury na zmiany ogólnego poziomu cen.

Na zakończenie zauważmy, że ponieważ WCD konstruowany jest w oparciu o stały koszyk, jest on dzięki temu mniej pracochłonny i dlatego też jest stosowany w dużo szerszym zakresie aniżeli deflator PNB. Wskaźnik WCD ma szerokie zastosowanie. Jest narzędziem indeksacji, zmienną obserwowaną przez decydentów gospodarczych i politycznych, na której opierają oni antycykliczne programy ekonomiczne. Poza tym WCD jest wykorzystywany przez związki zawodowe do tzw. korekty kosztów utrzymania. Najogólniej mówiąc jest on stosowany wszędzie tam, gdzie rośnie ogólny poziom cen, a zatem gdy zachodzi konieczność przeliczenia wielkości nominalnych na realne

Wielkości nominalne i realne

Wiele danych opisujących gospodarkę w szczególności dotyczy to różnego rodzaju agregatów jest wyrażonych w formie wartościowej. Ich zmiany wynikają zatem nie tylko ze zmian ich fizycznych rozmiarów(wolumenu) ale również ze zmian poziomu cen, którymi posługujemy się przy obliczaniu ich wartości. Analizują zatem dokonujące się w czasie zmiany pewnych kategorii ekonomicznych, takich jak chociażby: wartość produkcji, wartość wielkość kosztów, poziom dochodów społeczeństwa, czy wartość generowanych przez sektor prywatny zysków i wielu innych, musimy brać pod uwagę wpływ, jaki wywiera na ich wartość zmiany poziomu agregujących je cen .

Aby zatem móc określić faktyczną zmianę wyrażonej wartościowo kategorii musimy odróżnić od siebie wielkości nominalne i realne.

Wartości nominalne to wartości wyrażone w cenach bieżących ( obecnie obowiązujących na rynku). Przedstawiają one zatem wartość zmiennej ekonomicznej, której poziom zmierzono został pieniądzem o sile nabywczej z okresu, do którego się ona odnosi.

Wartości realne to wartości wyrażone w cenach stałych a więc w cenach z interesującego nas okresu minionego, który uznamy za bazowy. Inaczej mówiąc przedstawiają one wartości zmiennej ekonomicznej, mierzonej pieniądzem o sile nabywczej z jednego okresu m, przyjętego przez nas za bazowy.

Wskaźniki zmiany cen a siła nabywcza jednostki pieniądza

Siła nabywcza pieniądza, realna wartość pieniądza, to ilość dóbr i usług, którą można zakupić za określoną jednostkę pieniężną.

Jak mierzymy silę nabywczą jednostki pieniężnej?

Siłę nabywczą jednostki pieniężnej i jej zmiany można wyrazić w wielkościach absolutnych podając kolejno ilości każdego dobra jaką możemy w danym momencie kupić za jednostkę pieniądza. Dla lepszego zrozumienia, jak się to robi posłużymy się tabelą poniżej.

	Ceny			Siła nabywcza złotówki
	Rok bazowy 1995	1996	Wskaźnik ceny	1995	1996
Benzyna	1 zł/l	1,2 zł/l	1,2:1*100=120	1zł = 1l	1zł =0,8(3) l.
Mięso	10 zł/kg	8,0 zł/kg	8: 10*100= 80	1 zł =10dk	1zł =12,5 dk

Przyjmijmy, że w okresie bazowym 1995 cena benzyny wynosiła 1 zł/l.. Siła nabywcza jednej złotówki, mierzona ilością benzyny, jaką można było za nią kupić, wynosiła w tym okresie

1 zł.=1 litr

W roku 1996 cena ta wzrosła do 1,2 zł/l. W nowych warunkach za jedną złotówkę możemy było kupić mniej bo tylko

1zł :1,2 zł/l = 0,8(3)l.

Wzrost ceny benzyny spowodował zatem w badanym okresie spadek siły nabywczej jednej złotówki liczonej ilością litrów jakie można z nią kupić

Do identycznych ustaleń dojdziemy wykorzystując obliczony poniżej indeks ceny benzyny.

1,2 zł/l :1 zł/l *100=120 (zdrożała o 120-100=+20%)

Jeśli teraz jedną złotówkę z roku 1996 podzielimy przez niego a uzyskany wynik i przemnóżmy przez 100

(1zł:120 )*100=0,8(3) zł

to otrzymany w ten sposób wynik informuje nas, że za jedna złotówka z roku 1996 można kupić tyle benzyny co za 0,8(3) złotówki w roku 1995, a zatem siła nabywcza złotówki w 1996 spadła i stanowi obecnie tylko 0,8(3) siły nabywczej złotówki z przed zmianą cen czyli z roku1995.

Z powyższej tabeli tabelki wynika również, że w roku 1995 cena mięsa wynosiła 10 zł/kg , ale w następnym1996 roku nie wzrosła tylko spadła do 8 zł/kg. Mierzona ilością mięsa siła nabywcza złotówki wynosiła w 1995 r

10 zł= 1kg

1 zł= 10dkg

Natomiast w roku 1996 ilość mięsa, jaką można było za nią kupić wynosiła

8 zł= 1 kg

1 zł= 12,5 dkg

Spadek ceny mięsa spowodował zatem wzrost siły nabywczej jednej złotówki wyrażonej ilościach mięsa jaka można z nią kupić

Do identycznych wniosków dojdziemy, gdy posłużymy się wskaźnikiem zmiany ceny mięsa

8zł :10zł *100= 80 (staniało 80-100 = -20 % )

Dzieląc jedną złotówkę przez wskaźnik zmiany ceny mięsa otrzymujemy

(1 zł : 80 ) * 100=1,25zł

Otrzymany wynik informuje że za jedna złotówka z roku 1996 można kupić tyle samo mięsa, co w roku 1995 za 1,25 zł. .

Mierzona mięsem siła nabywcza złotówki wzrosła i stanowi obecnie 1,25 siły nabywczej złotówki z przed zmiany cen. Inaczej mówiąc licząc w mięsie jedna złotka z roku 1996 była warta tyle, co 1,25 zł w roku ubiegłym

Siła nabywcza jednostki pieniężnej jest zatem odwrotnością wskaźnika zmiany ceny danego dobra przemnożoną przez 100. Gdy wskaźnik ten rośnie siła nabywcza maleje. Na odwrót, gdy wskaźnik cen malej siła nabywca jednostki pieniężnej rośnie

Siła nabywcza jednostki pieniężnej a wskaźnik ogólnego poziomu cen

W obu przypadkach operowaliśmy koszykami składającymi się tylko z jednego dobra( albo benzyny albo mięsa) Realną siłę nabywczą złotówki 25 i jej zmiany mierzyliśmy przy pomocy tylko jednego dobra. Zauważmy jednak, że uzyskane w ten sposób informacje swą sprzeczne ze sobą Siła nabywcza pieniądza spada, gdy do pomiaru posługujemy się cenami benzyny, ale rośnie, gdy obliczamy ją w mięsie

A co robić jak mierzyć siłę nabywczą pieniądza w realnym świecie, w którym mamy do czynienia z ogromną ilością dóbr i usług, z których jedne drożeją inne w tym samym czasie tanieją, a ceny jeszcze innych pozostają niezmienione

W realnym świecie odwołujemy się nie do poszczególnych cen tylko do agregatowych wskaźników, np: wskaźnik cen detalicznych lub deflatora pokazujących zmiany ogólnego poziomu cen Siłę nabywczą jednostki pieniężnej Sn ustalamy dzieląc jedną złotówkę przez ten wskaźnik

1zł 1 zł

Sn= -------- ; lub Sn= ----------

WCD def

Z przedstawionego wzoru wynika ze ogólny poziom cen odzwier­ciedla odwrotność poziomu siły nabywczej. Wzrost ogólnego wskaźnika cen oznacza odpo­wiedni spadek siły nabywczej pieniądza, natomiast spadek ogólne­go wskaźnika cen powoduje odpowiedni wzrost siły nabywczej pieniądza.

W ujęciu statycznym (w określonym momencie) jest ona wyznaczona przez ceny towarów, w ujęciu dynamicznym (w czasie) zmiany siły nabywczej pieniądza są odwrotnie proporcjonalne do zmian wskaźnika ogólnego poziomu cen (stopy inflacji wzrost poziomu cen obniża siłę nabywczą pieniądza, spadek cen zwiększa ją. Dlatego miernikiem siły nabywczej pieniądza jest odwrotność wskaźnika ogólnego poziomu cen.

Wskaźniki cen a przeliczanie wartości nominalnych na realne i na odwrót

Znając dla badanego okresu wielkość deflatora lub innego wskaźnika zmiany ogólnego poziomu cen np. wskaźnika cen detalicznych itp., możemy bez trudu dowolną wartość nominalnej przeliczyć na realną.

Otrzymamy to mnożąc interesującą nas wartości nominalnej z danego okresu przez realną wartość złotówki, którą obliczamy dzieląc jednostkę pieniężna przez wskaźnik cen. Ponieważ siła nabywcza złotówki jest odwrotnością wskaźnika cen, zatem aby zatem jakąkolwiek wielkość nominalną przekształcić w realną musimy podzielić ją przez wskaźnik cena uzyskany wynik pomnożyć przez 100.

Wielkość nominalna

Wielkość realna = ------------------------- * 100

Wskaźnik cen

W poprzednich paragrafach zapoznaliśmy się z mierzeniem produkcji realnej na poziomie przedsiębiorstwa. Wróćmy na moment do naszego do naszego przykładu z zeszytami i segregatorami, Wskaźnik cen wynosi129 ,nominalna wartość produkcji w 1991 wynosi 2300 Mając te dane łatwo możemy obliczyć realną wartość produkcji i sprzedaży w 1991 .Wynosi ona :

(2300 zł :129)*100=1780 zł

Tę samą metodę można zastosować do obliczenia wartości realnego PKBr, gdy znamy np. wartość nominalnego PKBn ( np., 600 mld zł) oraz wartość deflatora def PKB ( np.120). Produkt realny obliczamy posługując się poznaną formułą

PKBn 600 mld

PKBr= ---------------* 100 = ---------- *100=500 mld

def PKB 120

Rzecz oczywista, że gdy znamy wartość deflatora i realnego PKB możemy bez trudu obliczyć wartość nominalnego PKB

PKBn=( Def :100 ) *PKBr=1,20* 500 mld=600 mld

Jeżeli do obliczeń posługujemy się deflatorem, wówczas siła nabywcza pieniądza odzwierciedla najbardziej ogólny wskaźnik cen.. Znajduje on zastosowanie przy obliczania realnej wartość agregatów, które są sumą wytworzonej w danym okresie produkcji takich jak: przedstawiony już Produkt Krajowy lub Narodowy, czy też bliźniaczych tożsamych z nimi agregatów, Dochód Krajowy albo Narodowy, które są sumą wszystkich zarobionych w danym okresie dochodów, to znaczy: płac, procentów, czynszów, rent i zysków.

Jeżeli jednak chcemy poznać realną wartość agregatów cząstkowych, przedstawiających poziom poszczególnych dochodów np: płace zyski, czynsze, renty, czy odsetki, inaczej mówiąc, gdy chcemy obliczać realne dochody, musimy zastosować bardziej szczegółowe metody pomiaru i obliczenia oparte na wskaźnikach cząstkowych, jak np. wskaźnik kosztów utrzymania, cen detalicznych, cen hurtowych. Dopiero tak przeprowadzone obliczenia wykazują zmiany siły nabywczej dochodów i ka­pitałów poszczególnych grup i warstw społeczeństwa.

Dochody nominalne i realne

Ludzie często ulegają iluzji pieniądza sądząc, że jeśli stojąca do ich dyspozycji ilość rośnie, to ich sytuacja ekonomiczna poprawia się, natomiast pogarsza się, kiedy maleje. Wynika to z fakty, iż nie dostrzegają różnicy między wielkościami nominalnymi i realnymi. Szczególnie wyraźnie zjawisko to występuje w przypadku dochodów pieniężnych.

Jednak we współczesnym świecie mamy w zasadzie do czynienia ze zjawiskiem stałego wzrostu ogólnego poziomu. W warunkach permanentnej inflacji ocena swojej sytuacji na podstawie dochodów nominalnych musi prowadzić do błędnych wniosków. Inflacja jak już wiemy zmniejsza siłę nabywczą pieniądza, a zatem to, że mamy więcej pieniędzy nie znaczy, że możemy za nie więcej kupić. Aby zatem mieć prawidłowe rozeznanie w swojej sytuacji powinniśmy obok wielkości nominalnych posługiwać się nie tylko wielkościami nominalnymi, ale również umieć liczyć wielkości realne.

Dochody nominalne to ilości pieniądza otrzymywane przez właścicieli czynników wytwórczych: płace, renty, czynsze, procenty i zyski. Dochody realne to ilości dóbr i usług, jakie można za nie kupić.

Płaca nominalna i realna

Złóżmy, że otrzymujemy stale i niezmiennie dochód, np. płacę w wysokości Vn=1 000zł miesięcznie. Czy za te pieniądze będziemy w stanie kupić zawsze tę samą ilość dóbr i usług konsumpcyjnych? To zależy od cen nabywanych przez nas dóbr i usług. Jeśli w całym interesującym nas okresie pozostają one niezmienione, czyli gdy wskaźnik cen jest równy 100, to siła nabywcza złotówki nie zmienia się, płaca nominalna i realna są identyczne. Jeżeli jednak, co jest niestety smutną rzeczywistością, ceny kupowanych przez nas produktów rosną, siła nabywcza złotówki spada i za nasze dochody nominalne możemy realnie kupić coraz, mniej. W tej sytuacji nasza płaca realna maleje, choć płaca nominalna pozostaje bez zmian.

Jak przeliczamy pacę nominalną na realną ?

Aby obliczyć poziom płacy realnej Vr danym okresie musimy obliczyć się nabywczą dzisiejszej złotówki w stosunku do złotówki przed zmianą cen i uzyskaną wielkość przemnożyć przez płacę nominalną. Jeżeli wskaźnik ogólnego poziomu cen jest większy od 100 i wynosi np. WCD=I20, to obecna siła nowej złotówki wynosi:

(1zł :120 )*100=0,8(3) zł.

złotówki z okresu bazowego Płaca realna w przeliczeniu na złotówki okresu wyjściowego

Vr=1 000* 0,8(3)= 833 zł

Identyczny wynik uzyskamy, gdy płacę nominalną podzielimy przez wskaźnik ogólnego poziomu cen np. indeks cen detalicznych WCD, a uzyskany wynik pomnożymy przez sto.

Vn 1 000 zł.

Vr= ---------*100 = ------------*100=833 zł

WCD 120

Jeżeli np. w interesującym nas okresie płaca nominalna Vn= 1 000 zł. i pozostaje na niezmienionym poziomie, natomiast wskaźnik WCD=120 to nasza płaca realna wynosi obecnie Vr=(1000:120)*100=833.

Wynika z tego, że wzrost ogólnego poziomu cen wpływa, ujemnie na poziom płac realnych a spadek cen dodatnio

Zbadajmy, co działoby się z płacami realnymi, gdyby dwudziestoprocentowemu wzrostowi cen towarzyszył dwudziestoprocentowy wzrost płacy nominalnej.

1000+20%*1000 1200

Płaca realna =-----------------------*100 =-----------* 100=1000

120 120

Wynika z tego, że wzrost cen neutralizuje pozytywne skutki wzrostu płac nominalnych a zatem nie każdy wzrost płacy nominalnej prowadzić musi jednoznacznie do wzrostu płacy realnej. Gdy ceny rosną w takim samym tempie jak płace nominalne płaca realna pozostaje, niezmieniona.

Aby płaca realna rosła płaca nominalna musi rosnąć szybciej od wzrostu cen. Aby zatem obliczyć, czy i o ile płace realne rosną musimy tempo wzrostu płacy nominalnej skorygować o tempo wzrostu cen

Jako przykładem posłużmy się danymi dotyczącymi przeciętnego wynagrodzenia miesięcznego netto w Polsce w latach 1996 - 1997.

Dane:

Średnie miesięczne wynagrodzenie w 1996 710, 46 zł

Średnie miesięczne wynagrodzenie w 1997 872, 91 zł

Wskaźnik wzrostu cen (1996-1997) 114,9

Stopa inflacji za lata 1996 - 1997 14,9%

W roku 1996 wynosiło nominalne wynosiło 710, 46 zł, zaś rok później 872,91 zł. Na podstawie tych danych ( wartości nominalnych) obliczamy wskaźnik wzrostu wynagrodzenia (872,91:710,46)*100 = 122,9 Oznacza to, że przeciętne wynagrodzenie nominalne wzrosło w badamy okresie ( o 22, 9 % ) .

Aby obliczyć, czy o ile i jak zmieniło się wynagrodzenia realne musimy w pierwszej kolejności obliczyć wynagrodzenia realne w 1997 r

Vn 872,91

Vr= ---------*100=- ---------- -*100=759,72

WCD 114,9

Znając poziom płac realnych w obu okresach możemy obliczyć indeks ich zmian

(759,72 zł: 710, 46 zł)*100=106,9

Z obliczeń wynika, że płace realne wzrosły w ciągu badanego okresu nie, o 22,9 % lecz jedynie o 6,9%.Identyczne rezultaty uzyskanym posługując się formuła na obliczenia tempa wzrostu

ΔVr=759,72 zł -710, 46 zł =49,26zł

ΔVr /Vr =49,26zł: 710, 46 zł*100=6,9%

Podobny, choć mniej dokładny wynik uzyskamy, gdy dysponujemy tylko informacjami o tempach wzrostu pałac nominalnych i tempie wzrostu cen.. Wystarczy od tempa wzrostu płac nominalnych odjąć tempo wzrostu cen

22,9%- 14,9% =8%

Dokładny wynik uzyskamy dopiero wtedy, gdy zastosujemy poniższą formułę

100+22,9

-------------- *100=106,9

100+14,9

W analogiczny sposób obliczamy zachowanie się w warunkach inflacji pozostałych dochodów jednym z dochodów są płacone przez banki odsetki od pożyczonego kapitału pieniężnego. Ich wysokość wyznaczona jest przez poziom stopa procentowa. Ze względu na znaczenie tej kategorii przyjrzyjmy się bliżej pojęciu nominalnej i realnej stopy procentowej

Nominalna i realna stopa procentowa

W ekonomii musimy umieć odróżnić nominalną i realną stopę procentową od udzielonych pożyczek. Nominalna stopa procentowa informuj zarówno udzielającego jak i zaciągającego pożyczkę o ile procent powiększa się zwracana ilość pieniądza. Jest to ważna, ale niewystarczająca informacja.

Udzielający pożyczki chciałby np. wiedzieć czy otrzymana z procentem kwota pozwoli mu kupić więcej niż przed jej udzieleniem, czyli czy udzielenie pożyczki przyniesie mu realną korzyść, czy nie zdąży się, że kupi za nią mniej, czyli czy nie grozi mu strata. Więcej pożyczkodawca chce wiedzieć nie tylko czy, ale o ile więcej konkretnych dóbr i usług będzie mógł kupić. Jeśli przewidywana ilość jest zbyt mała może nie wyrazić chęci udzielenia pożyczki.

Pożyczkobiorca z kolei musi wiedzieć, czy będzie w stanie sprostać wymaganiom pożyczkobiorcy, czy to, co na tej pożyczce zyska starczy mu, by ją zwrócić z procentem i jeszcze na tym zadawalająco zarobić.

Oba podmioty muszą, zatem w swoich kalkulacjach uwzględnić zmiany siły nabywczej pożyczanego pieniądza muszą, zatem powinni oni operować nie nominalną a realną stopą procentową,

Najprostszą metodą ustalania poziom realnej stopy procentowej jest odjęcie od stopy nominalnej tempa wzrostu cen. Jeżeli nominalna stopa procentowa wynosi R=15%, zaś stopa inflacji odpowiednio Π=10% to realna stopa inflacji Rr=15%-10%=5%.

Bardziej wyszukana i precyzyjniejsza metoda polega na obliczeniu wskaźnika zmiany wielkości nominalnej pożyczanego pieniądza. W tym celu do nominalnej stopy procentowej R=15% dodajemy 100. Uzyskany w ten sposób wskaźnik dzielimy przez wskaźnik wzrostu cen, który obliczamy dodając do 100 stopy inflacji Π=10% Uzyskany iloraz mnożymy przez sto i od uzyskanego w ten sposób wskaźnika odejmujemy sto.

15% +100 115

--------------- = ---- -- *100 = 104,5 -100=4,5%

10% +100 110

W identyczny sposób możemy obliczać realne wielkości i dynamikę pozostałych dochodów, czyli zysków, czynszów i rent

Zwróćmy wagę na fakt, że stopa procentowa podobnie jak inne( poza zyskiem) dochody jest nie tylko dochodem, ale jest ukształtowaną na rynku finansowym ceną wypożyczenia kapitału pieniężnego. Oznacza to, że rozróżnienie na wielkości nominalne i realne rozciągnąć można na wszystkie ceny

Latem 2004 r. przez media światowe i polskie przetoczyła się fala nerwowych, a niekiedy wręcz panikarskich spekulacji na temat wzrostu cen ropy naftowej i jego wpływu na gospodarkę światową oraz poszczególnych krajów i regionów. Warto jednak spojrzeć na wahania cen ropy naftowej w perspektywie historycznej. Jeżeli policzyć skumulowaną inflację przez 14 lat, jakie dzielą nas od 1990 roku (np. we Francji 25 proc.), to okaże się, że ropa naftowa w cenach stałych jest dziś tańsza niż na początku lat 90. Jeżeli cofniemy się jeszcze dalej, do krytycznego roku 1979, to okaże się, że po to, by osiągnąć cenę porównywalną z ówczesną, ropa naftowa powinna dziś kosztować pomiędzy 90 a 100 dolarów za baryłkę.

Zob A. Koźmiński : Gra na emocjach Rzeczpospolita 02.10.04 Nr 232

Nominalne i realne zmiany cen

W analizach mikroekonomicznych przyjmujemy najczęściej, że cena interesującego nas dobra zmienia się tylko i wyłącznie pod wpływem zmian warunków rynkowych, natomiast nie uwzględniamy zmian będących efektem inflacji. Inaczej mówiąc prowadzimy analizę przy założeniu stałości ogólnego poziomu cen. W tych komfortowych warunkach, aby obliczyć jej procentowe zmiany wystarczy dwa poziomy, porównać ze sobą, otrzymany wynik przemnożyć przez sto w ten sposób otrzymujemy prosty indeks. Aby obliczyć zmiany procentowe, czyli tempo wzrosty lun spadku ceny danego dobra od wystarczy indeksu odjąć 100. Inny sposób polega na przemnożeniu przez sto wyniku porównaniu przyrostu ceny z jej wyjściowym poziomem.

Te dwa proste sposoby pozwalają ustalić czy i o ile procent zmieniła się cena interesującego nas wyrobu. Jednakże uzyskana w ten sposób informacja jest w niektórych sytuacja nie wystarczające. Posługując się tylko nią możemy ulec zjawisku iluzji pieniądza, czyli pomylić wzrost ogólnego poziomu cen będącego rezultatem inflacji ze wzrostem ceny interesującego nas dobra. Współczesny świat, to świat inflacji, czyli nieustannego wzrostu wszystkich cen. W świecie inflacji rosną wprawdzie ceny przeciętne tym nie wszystkie ceny rosną w takim samym stopniu. Jedne rosną wolniej zaś inne szybciej.. Aby zapobiec powstającym wskutek iluzji pieniądza nieporozumieniom, wprowadzimy do naszej skrzynki z narzędziami kategorią ceny realnej.

Deflator

CA= 125 Wskaźnik zmiany ceny dobra A dla roku 1995

C1 =120 Wskaźnik ogólnego poziomu cen dla roku 1995

CB =105 Wskaźnik zmiany ceny dobra B dla roku 1995

C0 =100 Wskaźnik ogólnego poziomu cen w bazowym roku 1990

1990 1995 Czas

Powyższy rysunek pozwoli nam lepiej wytłumaczyć to dość abstrakcyjne pojęcie. Z przedstawionych na nim danych wynika, że mierzony deflatorem ogólny poziom cen dla okresu wyjściowego 1990 C0= 100 wzrósł w roku 1995 do poziomu C1 = 120. Inaczej na to patrząc średni poziom cen podniósł się o 120-100= 20%. W tym samym okresie indeks prosty ceny dobra A wyniósł CA=125,czyli jego cena wzrosła o 25%,natomiast prosty indeks ceny dobra B wyniósł CB=105,czyli jego cena wzrosła o 5%

Istnieje prosty, ale niezbyt dokładny sposób ustalenia czy i o ile cena danego wyroby rośnie lub spada w porównaniu z cenami innych wyrobów. Możemy to ustalić odejmując od wartości prostego wskaźnik zmiany ceny danego dobra wartość mierzącego inflację wskaźnik zmiany ogólnego poziomu cen np. deflatora. Otrzymany wynik informuje, czy i o ile procent zmieniła się cena w porównaniu ze zmianami ogólnymi poziomu cen. W naszym przykładzie cena dobra A wzrosła realnie o 125-120=5% natomiast cena dobra B realnie spadała o 105-120=-15%.

Cena realna jest to kategoria ekonomiczna, która informuje nas, czy i o ile cena badanego wyrobu zmieniła się w stosunku do zmian ogólnego poziomu cen. Obliczmy ją jako stosunek prostego indeksu ceny danego dobra do wskaźnika wzrostu ogólnego poziomu cen np., wskaźnika wzrostu cen detalicznych, wskaźnika kosztów utrzymania, czy znanego na już wskaźnika wzrostu wszystkich cen, czyli deflatora a uzyskany w ten sposób wynik mnożymy przez sto

CAn

CAr= ------ * 100

def

Inaczej mówiąc jest wskaźnik realnej zmiany ceny badanego dobra. Jeżeli wartość prostego indeksu jest większa od wskaźnika ogólnego poziomu cen, uzyskana wielkość stosunkowa jest większa od jedności a po przemnożeniu przez sto uzyskujemy wskaźnik o wartości większej od stu .Tak wartość wskaźnika oznacza to,że cena interesującego nas dobra wzrosła szybciej niż wzrósł ogólny poziom cen. Oznacz to, że jego cena realna jego wzrosła lub inaczej mówiąc, że dobro to staje się w porównaniu z innymi droższe. Jeżeli natomiast wskaźnik zmiany ceny analizowanego dobra jest mniejszy od wskaźnika ogólnego poziomu cen jego cena rośnie wolniej od wzrostu ogólnego poziomu cen, jego cena realna spada, czyli staje się ono w porównaniu z innymi tańsze.

Nominalny i realny kurs wymiany walut

Jedną z cen jest kurs wymiany walut. Kurs wymiany walut jest rynkową cena waluty obcej wyrażonej w walucie krajowej lub cena waluty krajowej wyrażonej w walucie obcej. Na zakończenie tego podrozdziału wprowadzimy jeszcze jedno ważne rozróż­nienie dotyczące kursu walutowego. Chodzi o kurs nominalny i kurs realny. W tabeli kursów wymiany na początku rozdziału przedstawiono kursy wymiany nie uwzględniające zmian poziomu cen krajowych i zagranicznych. Są to kursy nominalne tj. wyrażoną w jednostkach pieniądza o wartości nominalnej bieżącej relacji wymiennej dwóch walut.

W ekonomii a szczególnie w makroekonomii posługujemy się często pojęcie realnego kursu wymiany walut. Aby obliczyć kursy realne musimy złotówkę i walutę zagraniczną w wyrażeniu nominalnym sprowadzić do ich realnej wartości z wybranego okresu bazowego.

Realny kurs walutowy jest to kurs nominalny skorygowany o zmiany cen (stopę inflacji) w kraju i za granicą. W sposób bardziej sformalizowaną definicję realnego kursu walutowego można zapisać następująco:

Ck

Kr = -----------• Kn.

Cz

gdzie:

Kr — kurs realny

Ck — wskaźnik wzrostu cen (inflacji ) towarów krajowych (np. w Polsce),

Cz — wskaźnik wzrostu cen(inflacji ) towarów w kraju, do którego porównujemy walu­tę krajową (np. do dolara w USA),

Kn — nominalny kurs krajowy, np. złotego do dolara.

Jeś1i np. ceny towarów wzrosły w Polsce w 1999 r. o 10%, a ceny towarów amerykańskich wzrosty tylko o 2%, zaś nominalny kurs złotego do dolara wy­nosił na początku 1999 r. 3,90 zł/$ , wówczas pod koniec 1999 r. realny kurs dolara wzrosłby do 4,20 zł/$

110

Kr= ------* 3,90 =4,20

102

Wykorzystana literatura

Begg D. i inni :Ekonomia PWE1993 t1

Bremond J.,Salort M.: Odkrywanie ekonomii. PWN 1994.

Bowden E. Bowden J: Ekonomia. Nauka zdrowego rozsądku Fundacja Innowacja Warszawa 2002 Dodatek matematyczny

Chiang A,C. : Podstawy ekonomii matematycznej PWE 1994

Czarny B. i inni: Podstawy ekonomii. PWE 1998

Czarny E., Nojszewska E.: Mikroekonomia PWE 1997

Domańska E.:Wokół interwencji państwa w gospodarkę PWN 1992

Encyklopedia Internetowa „Wiem” Portal ONET

Encyklopedia Internetowa „Interia ”Portal Wirtualna Polska

Garbicz M. : Wartość pieniądza w czasie SGH. Maszynopis powielany

Kuznetz S.: Wzrost gospodarczy narodów. Produkt i struktura produkcji Warszawa 1976

Matkowski Z.: Podstawy ekonomii. Mikroekonomia. WSZ i P im. B. Jańskiego 1999

Morris M. : Poradnik świeżo upieczonego menedżera Amber 2001

Nasiłowski M: System rynkowy Podstawy mikro-i makroekonomii. Key Text 2000

Nojszewska E.: Podstawy ekonomii. Wydawnictwa Szkolne i Pedagogiczne 1995

Nojszewska E. Szamrej Z :Mikroekonomia Kurs podstawowy) Fundacja Naukowa Taylora Zeszyty SGH 1991

Okólski M., Timofiejuk I: Statystyka ekonomiczna, Warszawa 1978;

Varian H.R.: Mikroekonomia Kurs średni, ujęcie nowoczesne PWE 1999 Dodatek matematyczny

Wiszniewski Z.: Mikroekonomia współczesna Syntetyczne ujęcie Centrum Edukacji i Rozwoju Biznesu Warszawa 1994

Zienkowski L. : Jak oblicza się dochód narodowy, Warszawa1971;

UNO. A System of National Accounts and Supporting Tables, New York 1952

PODSUMOWANIE I SYNTEZA

1. Aby zrozumieć, jak funkcjonuje gospodarka, potrzebujemy zarów­no teorii, jak i faktów. Nie ma żadnego pożytku z faktów bez porząd­kującej je teorii Teoria mówi nam, jakich faktów musimy szukać celu uzyskania prawidłowej odpowiedzi. Bez teorii zginęlibyśmy w powodzi informacji. Ale teoria nie poparta faktami staje się nie uzasadnionym niczym twierdzeniem.

2 Dane lub fakty empiryczne są niezbędne z dwóch powodów. Ujawniają one zależności, które powinniśmy wytłumaczyć. Ponadto, po sformułowaniu przez nas teorii, możemy posłużyć się danymi w celu weryfikacji naszych hipotez i kwantyfikacji efektów, jakie owe hipotezy implikują

3. Jedną z metod ekonomii jest obserwacja procesu gospodarowania. Polega ona między innymi na analizowaniu goto­wych zestawów liczbowych danych statystycznych dostarczanych przez wyspecjalizowane instytucje państwowe i międzynarodowe. Niektórzy ekonomiści jednak na własną rękę zbierają informacje o gospodarce.

3. Zebrane dane statystyczne przedstawiamy zwykle na kilka sposobów Najczęściej w postaci tablic i wy­kresów. Tablice służą do prezentowania danych w łatwo zrozumiałej formie.

4. Zawarte w tablicach dane statystyczne przedstawia się najczęściej w postaci szeregów czasowe lub prze­krojowych.

5. Szeregi czasowe to zbiór danych opisu­jące wartości określonej zmiennej ekonomicznej w różnych, najczęściej kolejnych, okresach. Prezentujemy je w formie wykresu ( np. liniowego lub słupkowego).Ich zaletą jest łatwość odczytania tendencji rozwojowej zmiennej. Ceną tego jest jednak utrata części informacji szczegółowych

6. Szeregi przekrojowe (ang. cross-section) odnoszą się do tego samego momentu i przedstawiają dane charakteryzujące różne jednostki np. osoby lub grupy osób należące do określonej populacji.Wygodną metodą ich prezentacji są np. wykresy kołowe.

7. Wykresy ułatwiają wyznaczenie tendencji rozwojowej określonej zmiennej, analizę struktury pewnych zjawisk oraz badanie zależności za­chodzących między różnymi zmiennymi Wykresy są często przydatne do konstruowania modeli

8. Wiele zmiennych zawartych w tabelach powiązane są ze sobą w sposób funkcyjny. Zależności funkcyjne przedstawiamy albo w postaci w postaci wzorów algebraicznych albo wizualnie w postaci wykresów

10. Chcąc ujawnić związek między zmiennymi, ekonomiści posługują się wy­kresami punktowymi. Parom zmiennych odpowiadają wówczas punkty wy­kresu. Zależność odkryta za pomocą wykresu punktowego może być liniowa lub nieliniowa. Osobno należy zbadać kierunek związku przyczynowo-skut­kowego, który może towarzyszyć korelacji statystycznej.

11. Zależność funkcyjna pomiędzy zmiennymi ekonomicznymi może być liniowa lub nieliniowa. Osobno należy badać kierunek zmian oraz siłę związku stopa zmian

12. Chcąc ujawnić związek funkcyjny między zmiennymi, ekonomiści posługują się wy­kresami punktowymi. Parom zmiennych odpowiadają wówczas punkty wy­kresu.

13. Wykres punktowy ukazuje zależność między dwiema zmiennymi przedstawionymi graficznie w układzie współrzędnych za pomocą nanie­sionych nań punktów o odpowiednich wartościach. Jeżeli punkty połączymy jedną wspólną linią, otrzymamy wykres liniowy

14. Wykresy planimetryczne ( dwuwymiarowe) pokazują zależność między dwiema zmiennymi przy założeniu pozostałych wielkości nie zmienionych ( klauzula ceteris paribus). Stosu­jąc tę metodę prezentacji zależności między zmiennymi, unikamy typo­wego dla przestrzeni dwuwymiarowej problemu pozostałych wielkości nie zmienionych.

15. Jeżeli chcemy uchylić założe­nie o stałości którejś z tych pozostałych wielkości, musimy przesunąć krzywą lub linię na wykresie.

16. Posługiwanie się dużą ilością danych szczegółowych bywa kłopotliwe. Z po­mocą przychodzą wtedy wielkości średnie. Na przykład, średnia arytmetyczna to suma wszystkich wartości zmiennej podzielona przez liczbę tych wartości. Posługiwanie się średnimi wygładza wahania analizowanej zmiennej.

17. Do oceny średnich rezultatów stosowane są również inne miary jak np. wartość modalna czy mediana

18. Wartości absolutne zmiennej wyrażone w konkretnych fizycznych jednostkach bezpo­średnio informują o jej poziomie. Informacji o stosunku absolutnej wielkości % zmiany zmiennej do jej poziomu z poprzedniego okresu dostarczają wartości względne

19. Wskaźnik to liczba pozostająca w takiej proporcji do stu, jak zmienna z okresu, do którego odnosi się wskaźnik, do zmiennej z wybranego arbitral­nie okresu bazowego. Wskaźniki wyrażają wartości względne w odniesieniu do wielkości bazowej. Posługiwanie się wskaźnikami pozwala szybko rozpo­znawać kierunek i rozmiary analizowanych zmian.

20. Wskaźniki (indeksy) wyrażają względne wartości danej zmiennej odniesione do pewnej wartości przyjętej za podstawę. Najczęściej stosowane są wskaźniki: natężenia struktury i dynamiki.

21. Wskaźniki opisujące udziały poszczególnych wielkości w całości to wskaźniki struktury

22. Wskaźniki opisujące zmiany określonej wielkości w czasie noszą nazwę indeksów dynamiki. Wskaźników dynamiki dzielimy na proste ( indywidualne) zespołowe ( agregatowe)

23. Wskaźniki indywidualne stosujemy dla badania dynamiki pojedynczych zmiennych

24 Wskaźniki agregatowe stosujemy, gdy mamy do czynienia z wartością wielu zmiennych dodanych do siebie

25 Wiele wskaźników odnosi się do średnich wyprowadzonych dla wielu zmiennych

26. Indeksy dynamiki dla agregatowe obliczamy porównując ze sobą wartości agregatów w obu okresach, a uzyskany wynik mnożymy przez 100.Tem[po wzrost wartości agregatu obliczamy odejmując od indeksu 100. Dodatnie tempo wystąpi wtedy,gdy wartość indeksu jest większa od 100

27. Na zmianę wartości agregatu wpływają jednoczenia zmiana fizycznych ilości (wolumenu) oraz zmiana cen używanych do agregacji. Wartość agregatu zmienia się( nawet gdy fizyczne ilości pozostają takie same), gdy w badanym okresie zmienią się ceny .Gdy ceny rosną wartość agregatu rośnie wraz z nimi i na odwrót. Stawia to pod znakiem zapytania informację o rzeczywistych zmianach agregatu

28. Aby wyeliminować wpływ zmiany cen na wartość agregatu,należy wartość agregatów w obu okresach obliczyć w tych samych cenach.Ceny te nazywanym stałymi lub bazowymi

29. Jeżeli wartość agregatu z okresu bieżącego podzielimy przez wartość agregatu z i okresu stanowiącego podstawę porównań, to otrzymamy oczyszczony z wpływu cen wskaźnik realnej zmiany agregatu

30. Wartość agregatu może być wyrażona w cenach bieżących ( nominalna) lub w cenach z okresu bazowego (realna).

31. Jeżeli wartość nominalną agregatu podzielimy przez jego wartość realną a uzyskany wynik pomnożyć przez 100, to otrzymamy wskaźnik przeciętnego wzrostu cen dóbr wchodzących w skład agregatu

32. W analizach makroekonomicznych posługujemy się bardzo dużymi agregatami Agregat, który obejmuje wszystkie wyprodukowane w danym okresie dobra i usługi nazywany jest produktem globalnym PG. Wskaźnik przedstawiający zmiany ogólnego poziomu cen dóbr wchodzących w jego skład nazywany jest deflatorem PG Podobne deflatory można obliczać dla innych dużych agregatów

33. Wartość tego wskaźnika informuje o zmianach przeciętnego poziomu cen z uwzględnianiem wagi jak w agregacie maja poszczególne elementy, a zatem jest on obliczany jako średnia ważona

34. Wskaźniki przyjmują niekiedy formę średniej ważonej innych wskaźników. Jest tak m.in. w przypadku wskaźnika przeciętnego poziomu cen detalicznych towarów konsumpcyjnych. W tym przypadku wpływ cząstkowych wskaź­ników wzrostu poszczególnych cen na poziom wskaźnika syntetycznego powinien być proporcjonalny do udziału wydatków na dane dobro w całości wydatków konsumentów na wszystkie dobra. Dzięki temu wskaźnik syn­tetyczny dobrze informuje o zmianach kosztów utrzymania.

35. W praktyce gospodarczej używane są inne wskaźniki średnioważone cen oparte na koszykach. Jest nim m.in. wskaźnik przeciętnego poziomu cen detalicznych ( WCD) towarów konsumpcyjnych.

36. Wskaźnik cen detalicznych (WCD) ilustruje zmiany cen wszystkich towarów kupowanych przez gospodarstwa domowe. We wskaźniku tym cena każdego towaru jest ważona udziałem tego towaru w budżecie typowego gospodarstwa domowego.

37. We wskaźniku tym wpływ cząstkowych wskaź­ników wzrostu poszczególnych cen na poziom wskaźnika syntetycznego jest być proporcjonalny do udziału wydatków na dane dobro w całości wydatków konsumentów na wszystkie dobra. Dzięki temu wskaźnik syn­tetyczny dobrze informuje o zmianach kosztów utrzymania.

38. Wskaźnik cen detalicznych wyraża ogólną tendencję zmian cen towarów i usług nabywa­nych przez gospodarstwa domowe.

39.Jeżeli od wartości tego wskaźnika odejmiemy 100,to otrzymana różnica informuje nas o tempie wzrostu cen, czyli o stopie inflacji

40. Roczna procentowa zmiana wskaźnika cen detalicznych jest po­wszechnie stosowaną miarą inflacji, tj. stopy zmian cen.

41. Siła nabywcza jednostki pieniądza oznacza ilość dóbr konsumpcyjnych, którą przeciętnie można za nią nabyć.

42. Zmienna ekonomiczna jest zmienną nominalną, jeśli jej poziom zmierzono w jednostkach pieniądza o sile nabywczej z okresu, do którego zmienna ta się odnosi, a zmienną realną, jeśli jej poziom zmierzono w jednostkach pieniądza o ustalonej sile nabywczej z jednego, wybranego okresu.

43. Nominalne lub bieżące wartości zmiennych to wartości obliczane według cen występujących w okresie, kiedy pomiar zmiennej miał miejsce. Realne lub stałe wartości zmiennych to wartości obliczane metodą korygowania wartości nominalnych w taki sposób, aby wyelimi­nować wpływ zmian cen (inflacji).

44. Dochód nominalny to suma otrzymywanych pieniędzy. Dochód realny kontowaniem

45. Ceny realne (względ­ne, inaczej relatywne) są miarą względnej rzadkości dóbr w gospodarce. Cena realna to cena nominalna podzielona przez wskaźnik cen i przemnożona przez 100

46 Aby obliczyć wartość przyszłą posługujemy się procentem składanym

47 Dla obliczenia wartości zaktualizowanej wykorzystujemy metodę dyskonta

48 Im wyższa stopa procentowa i im dłuższy czas tym współczynniki dyskonta mniejszy, tym niższa jest wartość zaktualizowana

49 W warunkach inflacji przewidywana stopa inflacji zmniejsza wartość współczynników dyskonta a tym samym wartość zaktualizowaną

Wykorzystana literatura

Begg D. i inni :Ekonomia .PWE1993 t 1 roz.2

Bremond J.,Salort M. :Odkrywanie ekonomii .PWN 1994.

Bowden e. Bowden .J Ekonomia .Nauka zdrowego rozsądku Fundacja Innowacja Warszawa 2002 Dodatek matematyczny

Chiang A,C. Podstawy ekonomii matematycznej PWE 1994 roz.2

Czarny B. i inni :Podstawy ekonomii. PWE 1998 roz.2

Encyklopedia Internetowa „ Wiem „ONET

Encyklopedia Internetowa „Interia „ Wirtualna Polska

Garbicz M. Wartość pieniądza w czasie SGH Maszynopis powielany

Matkowski Z.: Podstawy ekonomii. Mikroekonomia. WSZiP im. B. Jańskiego 1999 roz.13

Morris M. Poradnik świeżo upieczonego menedżera Amber 2001

Nasiłowski M. System rynkowy Podstawy mikro-i makroekonomii. Key Text 2000 roz.15 s 338

Nojszewska E.: Podstawy ekonomii. Wydawnictwa Szkolne i Pedagogiczne 1995

Nojszewska E. Szamrej Z :Mikroekonomia Kurs podstawowy) Fundacja Naukowa Taylora Zeszyty SGH 1991 Dodatek

Varian H.R. Mikroekonomia Kurs średni ,ujęcie nowoczesne PWE 1999 Dodatek matematyczny

Wiszniewski Z. Mikroekonomia współczesna Syntetyczne ujęcie Centrum Edukacji i Rozwoju Biznesu Warszawa 1994 roz. 1

ENCYKLOPEDIA INTERNETOWA

Agregacja (aggregation) (łac. aggregatio - gromadzenie się) proces łączenia (skupiania) elementów w całość lub danych w zbiory mniej liczne, dzięki czemu otrzymuje się tzw. dane uogólnione lepiej charakteryzujące dany proces czy zjawisko. Dokonując agregacji należy dążyć do tego, aby strata informacji zawartych w danych pierwotnych była jak najmniejsza. Agregacja danych jest bardzo ważnym procesem w analizie systemowej. Jest ona szeroko stosowana w ekonomii, gdzie operuje się wartościami zagregowanymi (np. agregatami wartościowymi). Działaniem odwrotnym do agregacji jest dysagregacja (dekompozycja).

Dane statystyczne pierwotne, informacje statystyczne uzyskane bezpośrednio od badanych jednostek w trakcie badań statystycznych:

a) planowanych przez organa statystyki państwowej,

b) przeprowadzanych przez instytucje i osoby zajmujące się zawodowo statystyką,

c) mających wyraźnie sprecyzowany przedmiot badania, określoną jednostkę oraz technikę badania.

Danych pierwotnych dostarczają spisy, rejestry, ankiety itp.

Dane statystyczne wtórne, dane uzyskiwane bez przeprowadzania specjalnych badań statystycznych. Powstają w toku pracy różnych instytucji, które nie zajmują się zawodowo statystyką, np. wszelkiego rodzaju ewidencje prowadzone w urzędach, sądach w celach dokumentalnych, dane księgowości, wykazy wymiaru podatków, rejestry dochodzeń policyjnych itp. Odzwierciedlają najczęściej jedynie formalny stan prawny.

DECYL [łac.], statyst. kwantyl rzędu i/10, gdzie i = 1, ..., 9.

Deflator cen (produktu narodowego brutto) (price deflator), przelicznik obejmujący zmiany cen wszystkich wytworzonych w danym okresie dóbr i usług finalnych, tj. dóbr konsumpcyjnych, inwestycyjnych, surowców, produktów przemysłowych, produktów rolnych itp. Deflator cen produktu narodowego brutto wyraża koszt nabycia dóbr i usług finalnych uwzględnionych w tym produkcie w wybranym roku w stosunku do kosztu nabycia tych samych pozycji w roku podstawowym (bazowym). Zastosowanie deflatora cen umożliwia porównywanie wartości względnych (realnych), a nie absolutnych (nominalnych) i powoduje, że zmiany produktu narodowego brutto w czasie odzwierciedlają zmiany rzeczywistej produkcji, a nie zmiany poziomu cen.

Dyskonto,

1) odwrotność procentu składowego. Technika pozwalająca określić aktualną wartość przyszłych (oczekiwanych) dochodów. Polega na przemnożeniu tych dochodów w kolejnych latach przez współczynnik dyskontowy a_t = 1/(1+r)^t.

Znajduje zastosowanie m.in. w rachunku ekonomicznej efektywności inwestycji i procesach wyceny kapitału.

2) potrącenie odsetek przy zakupie papieru wartościowego (np. weksla) przed upływem terminu jego płatności.

Operacje dyskontowe są jednym z rodzajów czynnych operacji bankowych. Przy obliczaniu wartości kupowanego weksla wykorzystuje się podany wyżej współczynnik.

3) różnica pomiędzy wysokością zobowiązania płatnego w przyszłości i ceną, po jakiej wierzyciel odstępuje je przed terminem spłaty. Różnica ta stanowi kwotę odsetek przypadającą następnemu wierzycielowi za okres od chwili nabycia do momentu spłaty zobowiązania. Podstawą obliczenia dyskonta jest istniejąca w danym kraju stopa dyskontowa

Funkcja (function) Zbiór (zakres) potencjalnych (możliwych), zwykle powtarzalnych, typowych i sformalizowanych proceduralnie działań, wyodrębnionych ze względu na ich zawartość treściową (rodzaj) oraz na ich zrelatywizowanie do określonego celu lub jego części (zadania).

W znaczeniu potocznym funkcja oznacza określoną pracę, obowiązki, które ktoś ma wykonać a także stanowisko, które ktoś zajmuje

GŁÓWNY URZĄD STATYSTYCZNY, GUS naczelny organ statystyki państwowej w Polsce; utworzony 1918, wznowił działalność 1945, działa przy Radzie Ministrów; do podstawowych zadań GUS należy prowadzenie badań statystycznych dotyczących życia społeczno-gospodarczego, koordynacja sprawozdawczości statystycznej w kraju, prowadzenie spisów powszechnych i gromadzenie dokumentacji statystycznej dot. kraju i zagranicy, udostępnianie danych, w tym publikacje z zakresu statystyki (m.in. Roczniki statystyczne).
GŁÓWNY URZĄD STATYSTYCZNY (GUS), nacz. organ statystyki państw. w Polsce, utworzony 1918; jego organizatorem był L. Krzywicki; po przerwie w działalności, w okresie II wojny świat. 1945 reaktywowany jako centr. organ administracji państw. w zakresie statystyki; działania GUS obejmują przede wszystkim: prowadzenie statyst. badań życia gosp., społ. i kult. oraz opracowywanie i ogłaszanie wyników tych badań, przeprowadzanie spisów powszechnych; GUS zbiera, opracowuje i ogłasza wyniki badań w zakresie statystyki międzynar., bierze udział w pracach organizacji międzynar. w dziedzinie statystyki; prowadzi badania nauk. w zakresie metodologii statystyki; publikuje m.in. „Rocznik Statystyczny” oraz „Mały Rocznik Statystyczny”, „Wiadomości Statystyczne” i „Zeszyty Statystyki Polskiej”.

Indeks, liczba względna charakteryzująca zmiany poziomu zjawiska zachodzące w czasie. Indeks oblicza się zwykle w procentach w stosunku do wielkości danego zjawiska w okresie przyjętym za podstawowy.

Rozróżnia się indeksy indywidualne (proste), oparte na zmianach jednej wielkości, związane z obliczeniami dotyczącymi całej zbiorowości oraz indeksy zespołowe (agregatowe), oparte na zmianach zespołu wielu wielkości, związane z obliczeniami dotyczącymi zbiorowości cząstkowych.

Indeks cen (price index), procentowy wskaźnik zmiany przeciętnego poziomu cen w danym okresie. W statystyce oblicza się trzy rodzaje tego wskaźnika: indeks cen konsumpcyjnych (detalicznych), indeks cen hurtowych i indeks cen produkcyjnych. Indeks cen konsumpcyjnych jest najczęściej stosowaną miarą inflacji, która określa tzw. stopę inflacji (inflation rate) wyrażającą zmiany poziomu cen i mierzoną właśnie wskaźnikiem cen lub deflatorem.

Indeks kosztów utrzymania (cost of living index), miara poziomu siły nabywczej pieniądza w danym okresie czasu. Za podstawę indeksu cen służy stały "koszyk towarów" opracowany dla rynku bazowego przez Główny Urząd Statystyczny. Koszyk ten jest reprezentatywny dla przyzwyczajeń i gustów społeczeństwa. Wzrosty cen w danym roku porównywane są do poziomu cen roku bazowego. Indeks ten służy do porównań cen dóbr i usług nabywanych przez standardowe gospodarstwo pracownicze dla pokrycia potrzeb życiowych. Kształtowanie się tego wskaźnika może stanowić podstawę dla podejmowania decyzji co do zmiany (rewaloryzacji) płac i świadczeń społecznych.

Indeksacja (indexation), zastrzeżenie wobec płac i innych umów, na mocy którego wartości nominalne są często dostosowywane do zmian któregoś wskaźnika cen i utrzymywana jest realna wartość postanowień umowy.

Indeksacja płac jako proces ciągłego dostosowywania płac do wzrostu cen i kosztów utrzymania spełnia głównie funkcje dochodowe i ochronne. Jej podstawą jest indeks wzrostu cen artykułów i usług nabywanych przez ludność. Indeksacja może być wprowadzona na mocy ustawy, której celem jest ochrona dochodów przed inflacją.

W znaczeniu ogólnym termin "indeksacja" oznacza pewien system powiązania płac, cen, stóp procentowych itp. w postaci indeksu, powodujący automatyczny wzrost lub spadek tych kategorii.

Indeksacja, system (procedura) przywiązywania płac, cen, stóp procentowych itp. do danego indeksu. Powoduje tym samym automatyczny wzrost lub spadek wyżej wymienionych kategorii. Stosowana przy określaniu poziomu dochodów w celu zmniejszenia poziomu uciążliwości inflacji.

Kapitalizacja (z łaciny capitalis - główny), gromadzenie kapitału w celu późniejszego wykorzystania go do osiągnięcia jakiegoś celu działalności gospodarczej.

Kapitalizacja odsetek, powiększanie podstawy naliczania odsetek od pieniędzy złożonych na rachunku bankowym. Odsetki nie wybrane przez klienta po określonym okresie oszczędzania zostają dopisane do kwoty podstawowej, wpłaconej na początku i suma kwoty początkowej plus odsetki od niej stanowią w następnym okresie podstawę do naliczania nowych odsetek.

Kwantyl, mat., statyst. parametr służący do opisu: 1) populacji — taka liczba x_q, że 100 % elementów danej populacji ma wartość badanej cechy nie większą od x_q; 2) rozkładu prawdopodobieństwa — taka liczba x_q, że prawdopodobieństwo przyjęcia przez daną zmienną losową wartości nie większej od x_q jest równe q; w obu przypadkach mówi się o k. rzędu q (0 < q < 1); zob. też decyl, kwartyl, mediana.

KWARTYL, statyst. kwantyl rzędu 0,25 (dolny k.) lub 0,75 (górny k.).

LEIBNIZ GOTTFRIED WILHELM (1646-1716), niem. filozof i matematyk; od 1673 czł. Tow. Król. w Londynie; założyciel (1700) Akad. Nauk w Berlinie; od 1700 czł. Akad. Nauk w Paryżu; od 1667 pracował w służbie dyplomatycznej Palatynatu. Leibniz był twórcą koncepcji filoz., wg której świat jest zbiorem monad, tj. substancji niematerialnych, niepodzielnych, pozbawionych części, a więc nie podlegających oddziaływaniom zewn., niezdolnych do wzajemnej komunikacji i spontanicznych w zachowaniu; monady, różniące się między sobą doskonałością (zdolnościami poznawczymi), tworzą strukturę hierarchiczną — od najniższych (ciała org.) do monady najwyższej (Bóg); działanie monad jest uporządkowane dzięki „harmonii wprzód ustanowionej”, którą stwórca świata założył w jego budowie. W zakresie badań logicznych Leibniz wysunął pomysł matematyzacji logiki, pojmowanej przezeń jako rodzaj rachunku, i postulował stworzenie uniwersalnego języka symbol. (ideograficznego) oraz sformułował zasadę racji dostatecznej; w matematyce odkrył (niezależnie od I. Newtona) rachunek całkowy i rachunek różniczkowy, zapoczątkował teorię styczności krzywych i teorię obwiedni, sformułował wiele pojęć matematycznych. W pracy Wzorzec dowodów politycznych (1669, wyd. pol. 1843, wyd. 2 1969) zajął się problematyką elekcji króla w Polsce w okresie bezkrólewia 1668-69. Główne prace filozoficzne Leibniz'a: De la tolérance des religions (1692), Nowe rozważania dotyczące rozumu ludzkiego (1704, wyd. 1765, wyd. pol. 1955), Essais de Théodicée sur la bonté de Dieu, la liberté de l'homme et l'origine du mal (1710), Zasady natury i łaski (1714, wyd. 1718) i Monadologia (1714), wyd. pol. w zbiorze pism filoz. Wyznanie wiary filozofa (1969).

S. CICHOWICZ Filozof i istnienie, Warszawa 1970;

M. GORDON Leibniz, Warszawa 1974;

K. KRAUZE-BŁACHOWICZ Leibniz, Białystok 1992

LICZB WIELKICH PRAWA, mat. twierdzenia teorii prawdopodobieństwa orzekające, że jeżeli pewna zmienna losowa X ma wartość oczekiwaną równą µ, to średnia arytmetyczna (X₁ + X₂ +... + Xn)/n niezależnych obserwacji X₁, X₂,..., X_n tej zmiennej losowej jest dla wielkich n w przybliżeniu równa µ. Szczególnym przypadkiem prawa wielkich liczb jest twierdzenie głoszące, że częstość, z jaką dane zdarzenie pojawia się w długim ciągu doświadczeń, jest w przybliżeniu równa prawdopodobieństwu tego zdarzenia. Najprostsze prawo wielkich liczb pojawiło się po raz pierwszy 1713 w pracach Jakoba Bernoulliego i orzekało, że jeżeli p jest prawdopodobieństwem pewnego zdarzenia losowego A oraz nA jest liczbą tych, spośród n, niezależnych eksperymentów (pomiarów, obserwacji), w których zdarzenie A wystąpiło, to dla każdej dodatniej liczby ε prawdopodobieństwo zdarzenia losowego — polegającego na tym, że częstość nA/n zdarzenia A różni się od p o więcej niż ε — dąży do zera, gdy liczba n eksperymentów rośnie do nieskończoności. Jest to jednocześnie najprostszy przykład tzw. słabego prawa wielkich liczb. Mocne prawo wielkich liczb w powyższej sytuacji orzekają, że z prawdopodobieństwem 1 częstość nA/n dąży do p (E. Borel, 1909). We współcz. teorii prawdopodobieństwa są znane różne uogólnienia prawa wielkich liczb.

Marshall Alfred (1842-1924), ekonomista i filozof angielski. Przedstawiciel kierunku subiektywistycznego (Neoklasyczna szkoła anglo-amerykańska). Absolwent uniwersytetu w Cambridge, wykładowca ekonomii na uniwersytecie w Bristolu, od 1883 profesor, a od 1885 kierownik katedry ekonomiki w King's College w Cambridge. Rozwinął teorię popytu, wprowadził do niej pojęcie elastyczności. Dokonując syntezy teorii popytu i podaży wyjaśnił współzależności pomiędzy popytem, podażą oraz działanie mechanizmu rynkowego. Rozwinął teorię podziału dochodu narodowego i teorię pieniądza, stając się twórcą dochodowej teorii pieniądza.

Autor cennych prac, m.in.: Ekonomika przemysłu (wspólnie z żoną - 1879), Zasady ekonomiki (1890), Przemysł i handel (1919), Pieniądz, kredyt i wymiana (1923).

MARSHALL Alfred (1842-1924)

ekonomista ang., prof. uniw. w Cambridge; współzał. British Economic Association (późniejsze Royal Economic Society); nawiązywał do dorobku klasycznej ekonomii angielskiej (A. Smith, D. Ricardo), zapoczątkował w ekonomii kierunek neoklasyczny; opracował i szeroko stosował metodę równowagi cząstkowej, analizował związek zachodzący pomiędzy podażą, popytem i ceną uznając, że popyt i podaż określają cenę, która ostatecznie wyrównuje obie te wielkości; wielkość popytu zależy, zdaniem M., od użyteczności krańcowej danego dobra, wielkość podaży od kosztów produkcji, które można sprowadzić do krańcowego wynagrodzenia czynników produkcji (pracy, kapitału, ziemi i organizacji); M. opracował "prawo elastyczności popytu", określające zależność zmian popytu pod wpływem zmian ceny. Poglądy M. wywarły silny wpływ na dalszy rozwój ekonomii. Gł. prace: Zasady ekonomiki; Industry and Trade; Money, Credit and Commerce.

Mediana, wartość środkowa, wartość cechy w szeregu uporządkowanym, powyżej i poniżej której znajduje się jednakowa liczba obserwacji. Mediana jest to wartość środkowa obserwacji w szeregu. Aby ją ustalić, dodajemy do liczby obserwacji 1 i sumę tę dzielimy przez 2.

Mediana [łac.] (wartość środkowa), mat., statyst. kwantyl rzędu 0,5, czyli: liczba znajdująca się w środku uporządkowanego niemalejąco zbioru n zaobserwowanych wartości danej cechy (gdy n jest liczbą parzystą — średnia arytmetyczna 2 środkowych wyrazów) oraz dla zmiennej losowej X — liczba x spełniająca warunek P (X ≤ x) = 1/2

Metoda reprezentacyjna, metoda statystyczna polegająca na wylosowaniu z badanej zbiorowości (Populacji) jej części (czyli próby) i oszacowaniu na podstawie danych próby parametrów populacji. Stosowana jest przede wszystkim w statystyce społecznej i ekonomicznej. Znajduje zastosowanie w tych przypadkach, gdy wyczerpujące badanie statystyczne jest niemożliwe lub zbyt kosztowne do przeprowadzenia, a na podstawie badania metodą reprezentacyjną można uzyskać wystarczająco dokładne oszacowanie parametrów populacji.

Modalna wartość, moda, dominanta, wartość najczęstsza statystycznie, parametr charakteryzujący rozmieszczenie (położenie) populacji. Dla rozkładu umiarkowanie asymetrycznego wartość modalną Mo oblicza się z przybliżonego wzoru Mo≈3Me-2m, gdzie: Me - mediana, m - wartość średnia badanej populacji.

Odsetki, dochód otrzymany przez pożyczkodawcę za rezygnację z dysponowania pożyczonym kapitałem; cena, jaką musi zapłacić pożyczkobiorca za możliwość uzyskania kapitału i swobodnego nim dysponowania.

Oprocentowanie, procent, forma dochodu od kapitału pożyczkowego, uzyskiwanego przez właścicieli kapitału w postaci pieniężnej z tytułu jego udostępnienia (pożyczenia) innym użytkownikom. Wysokość tego dochodu uzależniona jest od wartości pożyczki oraz od poziomu stopy procentowej.

POCHODNA FUNKCJI, mat. jedno z podstawowych pojęć rachunku różniczkowego: niech y = f(x) oznacza funkcję ciągłą i określoną w przedziale (a, b); jeśli argumenty x oraz x + Δx (Δx — przyrost) należą do przedziału (a, b) i jeśli istnieje granica [f(x + Δx) - f(x)]/Δx, to granicę tę nazywa się pochodną funkcji f(x) w punkcie x i oznacza symbolem f '(x) lub df(x)/dx; wyrażenie [f(x + Δx) - f(x)]/Δx nazywa się przy tym ilorazem różnicowym, a pochodną df(x)/dx ilorazem różniczkowym; geometrycznie pochodna funkcji f(x) przedstawia nachylenie stycznej, czyli tangens kąta α, który styczna do wykresu funkcji y = f(x) w punkcie P (x, f(x)) tworzy z dodatnim kierunkiem osi odciętych (osi x-ów); w różnych punktach pochodna f '(x) może mieć różne wartości, a więc odpowiadająca jej styczna do wykresu — różne nachylenia względem osi odciętych.

Jeśli funkcja y = f(x) ma w każdym punkcie pewnego przedziału pochodną, to mówi się, że funkcja ta jest w tym przedziale różniczkowalna, np. funkcja y = sin x jest różniczkowalna w przedziale (-∞, +∞) i jej pochodna wynosi cos x, w zapisie: (sin x)' = cos x; jeśli w danym przedziale funkcja jest różniczkowalna, to jest w nim ciągła, ale nie na odwrót (np. funkcja y = |x| jest ciągła w przedziale (-1, +1), ale nie ma pochodnej w zerze); jeśli w jakimś przedziale (a, b) pochodna f '(x) jest dodatnia (ujemna), to w tym przedziale funkcja f(x) jest rosnąca (malejąca); miejsca na osi odciętych, w których pochodna równa się zeru (f '(x) = 0), nazywają się punktami stacjonarnymi; o tym, jaki charakter ma dany punkt stacjonarny, decyduje druga (ewentualnie czwarta, szósta itd.) pochodna f ''(x), mianowicie: jeśli w danym punkcie stacjonarnym x₀ druga pochodna, f ''(x₀), jest dodatnia (ujemna), to w tym punkcie jest minimum (maksimum); jeśli zaś f ''(x₀) = 0, ale f '''(x₀) ≠ 0 (lub któraś dalsza pochodna rzędu nieparzystego jest różna od zera), to punkt P (x₀, f(x₀)) jest punktem przegięcia. Pochodne mają liczne zastosowania prakt., m.in. pomagają badać przebiegi różnych funkcji. W przypadku funkcji dwóch lub więcej zmiennych niezależnych wprowadza się pojęcie pochodnych cząstkowych względem każdej ze zmiennych niezależnych; np. funkcja u = x²y + y²z + z² x ma pochodne cząstkowe I rzędu: ∂u/∂x = 2xy + z², ∂u/∂y = x² + 2yz, ∂u/∂z = y² + 2zx, a pochodne II rzędu ∂ ²u/∂y² = 2z, ∂²u/∂z² = 2x, ∂²u/∂z ∂x = ∂²u/∂ x∂z = 2z itd.; pochodne typu ∂ ²u/∂x∂y, ∂ ³u/∂x∂y∂z, ∂³u/∂x ²∂z nazywają się pochodnymi mieszanymi; pochodne cząstkowe pozwalają również znajdować lokalne maksima i minima funkcji wielu zmiennych, przy czym sprawa jest tu nieco bardziej złożona.

Populacja,

1) w biologii grupa osobników tego samego gatunku (w obrębie której możliwa jest wymiana genów), zasiedlająca pewien obszar, izolowana barierami (genetycznymi, geograficznymi, etologicznymi) od innych podobnych grup, posiadająca specyficzne właściwości, takie jak liczebność populacji, zagęszczenie, tempo rozrodczości i śmiertelności, rozkład wiekowy (demografia) oraz sposób rozmieszczenia w przestrzeni.

2) wszyscy mieszkańcy w danym kraju albo na danym terenie. W szerokim rozumieniu każdy zbiór (nie tylko ludzi), z którego można pobrać próbę do badania.

PRAWDOPODOBIEŃSTWA RACHUNEK dział matematyki zajmujący się modelami probabilistycznymi, służący do badania zjawisk losowych i dostarczający sposobów obliczania prawdopodobieństw zdarzeń; podstawowym pojęciem r.p. jest prawdopodobieństwo przypisane zdarzeniom i spełniające określone aksjomaty, przy czym prawdopodobieństwa zdarzeń złożonych znajdujemy na podstawie znajomości prawdopodobieństw prostszych zdarzeń (tzw. elementarnych) o danych (w rozważanym modelu) prawdopodobieństwach. Jeśli wynikiem zdarzenia losowego w badanym modelu jest liczba (lub zespół liczb) to mamy do czynienia ze zmienną losową i jej rozkładem (prawdopodobieństw rozkłady); rozkład zmiennej losowej w pewnym stopniu opisują takie parametry jak: wartość średnia (przeciętna lub oczekiwana) oraz wariancja, a dokładnego opisu dostarcza dystrybuanta zmiennej losowej (jeśli jest znana dla danego zjawiska). Ważnym działem r.p. jest dział poświęcony tzw. twierdzeniom granicznym, opisujący rozkłady sum zmiennych losowych przy wzrastającej liczbie składników sumy; badanie tych twierdzeń zwróciło uwagę na fakt powszechnego występowania w przyrodzie rozkładu normalnego. Punktem wyjścia do stworzenia r.p. były próby zastosowania matematyki do gier hazardowych;.

PROCENT jedna setna (1/100) jakiejś wielkości, zwykle oznaczana symbolem %. (ekon.) 1. dochód z zainwestowanego kapitału pożyczkowego; 2. wynagrodzenie wierzyciela za odstąpienie na określony czas prawa dysponowania określoną kwotą pieniężną; 3. cena usługi świadczonej pożyczkobiorcy przez pożyczkodawcę w zamian za prawo do korzystania w ustalonym z góry okresie z danej sumy środków pieniężnych; 4. koszt operacji finansowej (z punktu widzenia pożyczkobiorcy), zależny gł. od wielkości pożyczonej kwoty i czasu dysponowania nią oraz wysokości przyjętej stopy procentowej; rozróżnia się: P. ZWYKŁY (PROSTY), stanowiący oprocentowanie wyłącznie kapitału początkowego, tj. bez powiększania tego kapitału o dochód uzyskany z niego w kolejnych okresach obliczeniowych; oraz P. SKŁADANY, który uzyskuje się przez naliczanie oprocentowania nie tylko względem kapitału początkowego, ale także kapitalizowanej sumy odsetek z kolejnych okresów obliczeniowych, np. po roku do kapitału podstawowego dolicza się ustalony w umowie dochód roczny z tego kapitału, a powstała w ten sposób kwota stanowi podstawę obliczenia dochodu po upływie następnego roku.

Procent składany, sposób oprocentowania kapitału, polegający na naliczaniu odsetek w kolejnych okresach umownych (najczęściej stosowane to: miesiąc, kwartał, pół roku i rok) od wartości kapitału początkowego powiększonego o kwotę odsetek należnych za okres poprzedni, czyli przy uwzględnieniu kapitalizacji odsetek.

Matematyczna formuła procentu składanego dla rocznego okresu kapitalizacji ma postać: K_n = K_o (1+r)ⁿ, gdzie: K_n - wartość kapitału po n latach, K_o - początkowa wartość kapitału, r - roczna stopa oprocentowania, n - okres, dla którego oblicza się procent składany.

Formuła ta pozwala obliczyć wartość kapitału, np. oszczędności w banku, którą będziemy dysponować po n latach lokując dziś kwotę K_o, przy rocznej stopie oprocentowania r. Przy okresie kapitalizacji krótszym od roku formuła procentu składanego przyjmuje postać: K_n,m = K_o(1+r/m)^nm, gdzie m jest liczbą okresów umownych mieszczących się w roku.

Redyskonto,

1) powtórne potrącenie odsetek od terminowych papierów wartościowych, których termin płatności jeszcze nie minął, przy zakupie ich przez bank centralny od banków handlowych, które wcześniej dokonały operacji ich dyskonta. Podstawą redyskonta jest ustalana przez bank centralny stopa redyskontowa, będąca jednym z narzędzi regulowania podaży pieniądza.

2) operacja zakupu przez bank centralny od banków handlowych terminowych papierów wartościowych przed upływem terminu ich wykupu przez wystawcę. Banki handlowe dokonują operacji redyskonta w celu zwiększenia swoich rezerw gotówkowych.

Reprezentatywna próba, część dużej zbiorowości statystycznej wylosowana zgodnie z określonymi zasadami matematycznymi. Ma takie same cechy, jak duża zbiorowość.

Reprezentacyjna metoda statystyczna, metoda szacowania wielkości liczbowych charakteryzujących zbiorowość statystyczną na podstawie wylosowanej lub wybranej części tej zbiorowości (tzw. próby reprezentatywnej).

Metoda ta, jako nie dość dokładna, znajduje zastosowanie wtedy, gdy badanie pełne jest zbyt kosztowne lub długotrwałe.

RÓWNANIE, mat. jedno z podstawowych pojęć mat.; równaniem nazywa się warunek zapisany w postaci równości, nakładany na niewiadome obiekty mat. (liczby, macierze, funkcje, operatory itp.); w zależności od natury niewiadomych obiektów mówi się o równaniach liczbowych, np.
, równaniach macierzowych, np.

,

równaniach funkcyjnych, np. f(x, y) = f(x) + f(y),

i równaniach operatorowych. Każdy obiekt, który spełnia rozważany warunek, nazywa się rozwiązaniem równania; równanie może mieć jedno lub wiele rozwiązań (również nieskończenie wiele), może też w ogóle nie mieć rozwiązań; rozwiązać równanie oznacza znaleźć wszystkie jego rozwiązania. Równaniem o jednej niewiadomej x jest równość dwu funkcji f(x) = g(x), rozważanych we wspólnej dziedzinie; równaniem o n niewiadomych x₁, x₂,..., x_n jest równość postaci f(x_1, x₂,..., x_n) = g(x₁, x₂,..., x_n). Rozważa się również układy równań, np. m równań z n niewiadomymi. Jeśli w równaniu f(x) = g(x) obie funkcje są wielomianami, to takie równanie nazywa się algebraicznym (m.in. równanie liniowe, kwadratowe, dwukwadratowe, sześcienne, diofantyczne), a jeśli któraś z funkcji jest przestępna, to równanie nazywa się przestępnym (m.in. równanie wykładnicze, logarytmiczne, trygonometryczne). W geometrii analitycznej równania interpretuje się jako określone zbiory punktów, np. równanie x² + y2 = 1 przedstawia okrąg o środku w punkcie (0, 0) i promieniu 1, równanie x + y + z = 1 przedstawia płaszczyznę, równanie x² + y² + z² = 9 przedstawia sferę o promieniu 3 i środku w punkcie (0, 0, 0). Każde dwa równania, które mają ten sam zbiór rozwiązań, np. sin x = 0 oraz |cos x| = 1, są równaniami równoważnymi

Siła nabywcza pieniądza, realna wartość pieniądza, ilość dóbr i usług, którą można zakupić za określoną jednostkę pieniężną. W ujęciu statycznym (w określonym momencie) jest ona wyznaczona przez ceny towarów, w ujęciu dynamicznym (w czasie) zmiany siły nabywczej pieniądza są odwrotnie proporcjonalne do zmian wskaźnika ogólnego poziomu cen (stopy inflacji): wzrost poziomu cen obniża siłę nabywczą pieniądza, spadek cen zwiększa ją. Dlatego miernikiem siły nabywczej pieniądza jest odwrotność wskaźnika ogólnego poziomu cen.

STATYSTYKA [łac.], pojęcie o przynajmniej 2 znaczeniach (M.G. Kendall i W.R. Buckland):

1) Numeryczne dane dotyczące agregatów złożonych z pewnych jednostek.

2) Nauka zajmująca się zbieraniem, analizą i interpretacją tego typu danych: w pierwszym znaczeniu statystyka jest utożsamiana z bazami danych liczbowych o obserwowanych zbiorowościach jednostek oraz o ich cechach statyst., w drugim obecnie jest utożsamiana z komputerowym przetwarzaniem baz danych liczbowych w postać ich syntet. charakterystyk liczbowych oraz w postać wnioskowania statyst. w warunkach niepewności. W ujęciu ogólnym statystyka jest więc dyscypliną nauki, która zajmuje się formułowaniem metod liczbowego przetwarzania indywidualnych informacji statyst. w celu opisu i wnioskowania statyst.; to ostatnie zajmuje się gł. procedurami estymacji (szacowania) parametrów oraz weryfikacji hipotez zerowych. Celem stosowania statyst. metod opisu i wnioskowania jest stworzenie możliwości przeprowadzania rzetelnej diagnostyki statyst. (jak jest i dlaczego tak jest?) oraz wysoce prawdopodobnej predykcji statyst. (jak by było przy spełnieniu określonych warunków?); diagnostyka i predykcja statyst. są określane jako analiza statystyczna. Umowną typologię analizy statyst. wg kryteriów formalno-statyst. oraz zakresowo-przedmiotowych zawiera tabela. Statystyka ma rozległe zastosowanie wszędzie tam, gdzie występują zjawiska i procesy masowe; badając zjawiska masowe (np. produkcję, zatrudnienie, płace, wzrost) obserwuje się w rzeczywistości zdarzenia losowe, których rozmiary liczbowe (realizacje zmiennych losowych) podlegają zarówno działaniu przyczyn gł. (wywołujących zmienność systematyczną), jak i ubocznych (wywołujących zmienność przypadkową). Stosowanie określonych metod statyst. (opisu i wnioskowania) na określonym polu ich użyteczności (struktura, korelacja, dynamika) umożliwiło powstanie specjalistycznych dyscyplin statystyki stosowanej, np. statystyki ekonomicznej, statystyki społecznej, statystyki medycznej, statystyki fizycznej, statystyki ludności Pierwotnie termin statystyka był używany na oznaczenie wiedzy o państwie; poczynając od najdawniejszych spisów w Egipcie i Chinach, poprzez rzym. cenzusy (spisy) i średniow. inwentaryzacje majątków feud. i kośc., najpierw słowny, a potem liczbowy spis statyst. służył gł. jako narzędzie w rękach władców i rządów państw. Prekursorami szerszego traktowania statystyki byli tzw. arytmetycy polityczni, a zwł. w XVII w. wybitni przedstawiciele tego kierunku — J. Graunt i W. Petty. Posługując się stosunkowo prostymi narzędziami opisu statyst. arytmetycy polit. wykazywali, że w pozornie chaotycznych, przypadkowych zjawiskach masowych występują określone regularności (prawidłowości). Tak powstał pierwszy uściślony tabelaryczny opis Rosji z 1726-27 (J.K. Kirgiłow) oraz Danii z 1741 (J.P. Anchersen); zapoczątkowano erę tabelaryzmu i arytmetyki polit. oraz sformułowano pierwsze proste uogólnienia teoret. dotyczące statystyki (K. Davenant, 1695). U podstaw współczesnej statystyki leży teoria rachunku prawdopodobieństwa, wyjaśniająca mechanizm, w jakim ujawniają się prawidłowości statyst. występujące w zjawiskach masowych. Rozwój teorii rachunku prawdopodobieństwa zapoczątkowali w 2 poł. XVII w. B. Pascal i P. Fermat, którzy pierwsi uzasadnili matematycznie prawidłowości występujące w grach hazardowych; sformułowane przez nich wstępne założenia i wnioski rozwijało wielu wybitnych teoretyków rachunku prawdopodobieństwa (probabilistów), przede wszystkim J. Bernoulli, który u schyłku XVII w. pierwszy sformułował i uzasadnił tzw. prawo wielkich liczb; stało się ono podstawą do udowodnienia przez A. de Moivre'a (koniec XVIII w.), P.S. de Laplace'a (pocz. XIX w.) oraz J.W. Lindberga i P. Levy'ego (lata 20. XX w.) tzw. lokalnego i centralnego twierdzenia rachunku prawdopodobieństwa. W XVIII i XIX w. powstały ważne dla statystyki odkrycia teoret., związane ze statyst. badaniami prowadzonymi metodą reprezentacyjną. Sformułowano wzór funkcji gęstości rozkładu normalnego zmiennej losowej ciągłej oraz rozkładu błędów losowych (Laplace i K.F. Gauss), nastąpiło wyodrębnienie składnika systematycznego i przypadkowego występujących w procesach zw. zjawiskami masowymi (Gauss) oraz określono prawo rzadkich zdarzeń (S. Poisson). Okres od końca XIX w. charakteryzował się wielką liczbą odkryć nowych metod i procedur badań statyst. (parametrycznych i nieparametrycznych); duży udział w tworzeniu dorobku metodologicznego statystyki mieli pol. statystycy, m.in.: M. Fisz, Z. Hellwig, J. Neyman, H.D. Steinhaus, S. Szulc. Współcześnie szczególnie wyraźne przyspieszenie rozwoju metod i procedur statystycznych badań wiąże się z szerokim zastosowaniem technik komputerowych. W Polsce badania statyst. są prowadzone przede wszystkim przez Główny Urząd Statystyczny, który koordynuje całokształt spraw związanych ze statystyką państwową (publ.).

M. FISZ Rachunek prawdopodobieństwa i statystyka matematyczna, Warszawa 1969;

J.E. FREUND Podstawy nowoczesnej statystyki, Warszawa 1971;

M.G. KENDAL, W.R. BUCKLAND Słownik terminów statystycznych, Warszawa 1986;

A. LUSZNIEWICZ Statystyka ogólna, Warszawa 1987;

C.R. RAO Statystyka i prawda, Warszawa 1991;

J. JÓŹWIAK, J. PODGÓRSKI Statystyka od podstaw, Warszawa 1992.

STATYSTYCZNE BADANIE, obejmuje 4 etapy: programowanie badania, obserwację statyst., opracowanie danych, analizę statystyczną.

Podstawą programowania jest specyfikacja jego ogólnych i szczegółowych celów, od których zależy sposób definiowania zbiorowości statyst. (generalnej lub próby losowej) oraz zakres obserwowanych cech ilościowych i jakościowych. Ważną czynnością etapu programowania badań statystycznych jest konstrukcja makiet tablic wynikowych (prostych i złożonych), wybór sposobów kontroli (eliminacji błędów) baz danych, określenie zakresu ich publikacji (udostępniania użytkownikom) itp. Na etapie tym jest niezbędna ścisła współpraca merytoryczna statystyków ze specjalistami w innych dziedzinach.Proces zbierania danych statyst. jest nazywany obserwacją empiryczną. Do najczęściej spotykanych jej form zalicza się obserwacje spisowe, bieżącą rejestrację oraz inne techniki (np. monitoring) o charakterze i przeznaczeniu specjalnym. Spisem statystycznym nazywa się liczbową charakterystykę badanej zbiorowości jednostek oraz wartości zmiennych cech statyst. w ściśle określonym momencie i na ściśle określonej przestrzeni; spis statyst. może być badaniem jednorazowym, powtarzanym lub nie powtarzanym okresowo; typowymi przykładami są coroczne spisy rolne oraz realizowane raz na ok. 10 lat powszechne spisy ludności i mieszkań; do obserwacji spisowych należy zaliczyć także ankietowe badania warunków bytu (poziomu i jakości życia) ludności (gospodarstw domowych), zw. mikrocenzusami społecznymi. Bieżąca rejestracja statystyczna jest prowadzona przez określone podmioty (przedsiębiorstwa, instytucje) w sposób ciągły i służy ich potrzebom oraz statystyce państw. (w Polsce GUS); o ile dane liczbowe bieżącej rejestracji statyst. są podstawowym źródłem wiedzy o zjawiskach i procesach gosp. kraju i jego regionów, o tyle gł. źródłem wiedzy o zjawiskach i procesach społ.-demograf. są obserwacje spisowe, a zwł. mikrocenzusy społ. i monitoring ludności (gospodarstw domowych). Badania o charakterze specjalnym ciągłe lub okresowe to np. obserwacje budżetów domowych, budżetów czasu, strefy ubóstwa itp.; często są one oparte na technikach ankietowo-retrospektywnych, samorejestracji i wywiadach uzupełniających; do technik tych można zaliczyć także tzw. szacunki statystyczne. Opracowywanie danych statystycznych, czyli ich przetwarzanie, jest zazwyczaj poprzedzone formalną i merytoryczną kontrolą zapisów liczbowych w bazach danych, ich symbolizacją (kodowaniem) i grupowaniem ze względu na podstawowe cechy statyst. o znaczeniu typologicznym oraz zaliczaniem jednostek zbiorowości w układach prostych (ze względu na jedną cechę) i w układach złożonych (ze względu na 2 i więcej cech); najpopularniejszą procedurą komputerowego przetwarzania danych statyst. jest pakiet Statgraphics; po wprowadzeniu danych indywidualnych i po dodatkowych operacjach (zakładanie, dzielenie i uaktualnianie zbiorów) pakiet ten oferuje m.in. następujące możliwości przetwarzania danych: metody opisu statyst., estymację i testowanie hipotez statyst., funkcje rozkładów zmiennych, analizę wariancji, analizę regresji, procedury analizy szeregów czasowych, analizę danych jakościowych.

Zasadniczym celem statystycznych badań jest analiza statystyczna, czyli integralnie traktowany opis statyst. i wnioskowanie statystyczne. Opis statyst. dotyczy zbiorowości generalnych (wszystkie jednostki) lub zbiorowości próbnych (wylosowane jednostki); wnioskowanie statystyczne dotyczy przypuszczeń o zbiorowościach generalnych, formułowanych na podstawie wyników uzyskanych z badań reprezentacyjnych; są one przenoszone na zbiorowości generalne na określonym poziomie precyzji statyst. (ufności oraz istotności). Metody wnioskowania statyst. są stosowane, gdy brakuje możliwości lub uzasadnienia, aby prowadzić pełną obserwację wszystkich jednostek tworzących zbiorowość generalną; istnieje możliwość, a nawet konieczność losowego doboru (na podstawie odpowiedniego schematu losowej lokalizacji) części jednostek zbiorowości generalnej, tworzących próbę losową i spełniających określone warunki zgodności strukturalnej względem zbiorowości generalnej. Próba losowa jest reprezentatywna, jeżeli jej struktura, ze względu na interesujące cechy statyst., jest co najwyżej losowo różna od struktury zbiorowości generalnej; pojęcie reprezentatywności prób losowych jest względne i odnosi się wyłącznie do tych cech statyst., które były podstawą konstrukcji operatu oraz schematu losowania jednostek. W praktyce badań statyst. metodą reprezentacyjną (np. w badaniach budżetów domowych prowadzonych przez GUS) chodzi o istotnie większą od przyjętej w losowaniu liczbę cech statyst., dlatego próby zw. doskonale reprezentatywnymi nie występują.

S. SZULC Metody statystyczne, Warszawa 1968;

M. KRZYSZTOFIAK Liczby, tablice, wykresy, Warszawa 1971;

R. KULCZYCKI Teoria i praktyka badania statystycznego, Warszawa 1971;

R. ZASĘPA Metoda reprezentacyjna, Warszawa 1972;

J. PODGÓRSKI Statystyka z komputerem. Pakiet „Statgraphics”, Warszawa 1993.

STATYSTYKA MATEMATYCZNA, dział matematyki zajmujący się metodami wnioskowania o własnościach populacji na podstawie losowych prób z tej populacji; wnioskowanie to polega na szacowaniu różnych parametrów populacji (estymacji teoria) lub na weryfikowaniu, za pomocą odpowiednich statystycznych testów, różnych hipotez o tych populacjach; pewne jednolite podejście do statystyki matematycznej proponuje teoria decyzji statystycznych; ze statystyki matematycznej wyodrębniły się wyspecjalizowane zespoły metod rozwijane jako biometria, epidemiologia, ekonometria, statystyczna kontrola jakości, teoria niezawodności i in.

Stopa dyskontowa, stopa procentowa stosowana w rachunku zaktualizowanej wartości przyszłych strumieni pieniężnych (płatności, dochodów). Praktyczne zastosowanie znajduje ona najczęściej w operacjach dyskonta terminowych papierów wartościowych (np. weksli), a także w niektórych metodach rachunku efektywności inwestycji oraz wyceny wartości kapitału rzeczowego i finansowego (w tym przypadku jej poziom jest przyjmowany przez zespół dokonujący tych rachunków, zazwyczaj w ujęciu wielowariantowym, w zależności od sytuacji na rynku kredytowym).

Wysokość stopy dyskontowej jest ustalana przez banki komercyjne dokonujące dyskonta terminowych papierów wartościowych i jest zawsze wyższa od stopy redyskontowej banku centralnego

STOPA PROCENTOWA stosunek sumy odsetek należnych w określonej jednostce czasu, np. przez rok (tzw. stopa roczna) do wartości kapitału (pożyczki, lokaty itp.), zwykle wyrażany w procentach; jest jednostkową ceną usługi płaconą przez pożyczkobiorcę pożyczkodawcy.

Stopa procentowa, wielkość mierzona procentowo wyrażonym stosunkiem kwoty, którą płaci się za użytkowanie kapitału pieniężnego do wielkości tego kapitału, najczęściej ustalana na okres roku.

Stopę procentową ustalają banki i określa ona, jaką sumę należy zapłacić za udzieloną przez niego pożyczkę lub jaką kwotę płaci bank klientowi za to, że przechowuje on swoje oszczędności w tym banku. Stopa procentowa w bankach komercyjnych oscyluje wokół poziomu ustalonego przez bank centralny. Jeżeli stopa procentowa wzrasta, to maleje popyt na kredyty, a wzrasta skłonność do oszczędzania i odwrotnie. Ustalanie przez bank centralny stopy procentowej jest jednym ze sposobów realizacji polityki monetarnej kraju. Wzrost stopy procentowej powoduje, że pieniądz odpływa z rynku do banków, co oznacza, że podaż pieniądza maleje i zmniejsza się ryzyko inflacji.

Średnia wartość, (przeciętna wartość), w statystyce miara przeciętnego poziomu mierzalnej cechy jednostek zbiorowości statystycznej. W zależności od celu badań lub rodzajów zbiorowości statystycznych do ich charakterystyki stosuje się wiele odmian średniej wartości.

Ich ogół dzieli się na średnie matematyczne, wśród których najczęściej stosowane są: średnia arytmetyczna, średnia geometryczna i średnia harmoniczna oraz średnie pozycyjne - dominanta i mediana.

Średnia arytmetyczna prosta , w statystyce suma wartości wszystkich jednostek zbiorowości statystycznej, podzielona przez liczebność tej zbiorowości (tj. liczbę tych jednostek). Wzór na średnią arytmetyczną ma postać:

X1+X2+.... +Xn

Sa = ----------------------------

n

gdzie: Sa - średnia arytmetyczna, x₁,x₂,...,x_n - poszczególne wartości pojedynczych jednostek zbiorowości statystycznej, n - ogólna liczebność badanej zbiorowości (tj. liczba wszystkich jednostek wchodzących w skład zbiorowości statystycznej).

Średnia arytmetyczna ważona

X1*W1 + X2* W2 + .... Xn*Wn

Sw = ------------------------------------------------

W1 + W2 + .... Wn

Gdzie Sw- średnia arytmetyczna ważona , X1+X2+.... +Xn zaobserwowane wartości zmiennych , W1 + W2 + .... Wn wagi ,(współczynniki wagowe ).Wagi mogą być definiowane w różny sposób w zależności od rodzaju badania ,częstości zachodzenia pwenego zjawiska ,wlumenu, wskaźnika udziału itp

Średnia geometryczna, w statystyce miara przeciętnego poziomu wartości cechy jednostek zbiorowości statystycznej używana dla cech przyjmujących wyłącznie wartości dodatnie.

Średnia geometryczna z dwóch liczb dodatnich jest pierwiastkiem kwadratowym z ich iloczynu. Ogólnie średnią geometryczną definiuje się jako pierwiastek N-tego stopnia z iloczynu wszystkich N wartości cechy:

Sg=

(X1 + X2 + X n)

gdzie: Sg - średnia geometryczna , x₁,x₂,...,x_N - wartości cechy jednostek n-elementowej zbiorowości.

Średnia harmoniczna, w statystyce rodzaj średniej wartości cechy jednostek zbiorowości statystycznej w przypadku cech nierealnych przyjmujących wyłącznie wartości dodatnie (lub wyłącznie ujemne). Średnia harmoniczna jest odwrotnością średniej arytmetycznej obliczonej z odwrotności wartości cechy:

n

Sh= ----------------

n 1

Σ ----

i=1 Xi

gdzie: Sh - średnia harmoniczna x_i = x₁,x₂,...,x_n - wartości cechy n-elementowej zbiorowości.

Średnia kwadratowa, w statystyce pierwiastek kwadratowy ze średniej arytmetycznej kwadratów wartości jednostek zbiorowości statystycznej:

( X1
+ X2
+ Xn
)

Sk= -------------------------

n

gdzie: Sk - średnia kwadratowa, x₁,x₂,...,x_n - poszczególne wartości pojedynczych jednostek zbiorowości statystycznej, n -

ogólna liczebność badanej zbiorowości.

Statystyka, nauka zajmująca się ilościowymi metodami badania prawidłowości zjawisk (procesów) masowych. Jej celem jest poznanie występujących prawidłowości, ich ilościowe wyrażenie oraz wyodrębnienie w nich składnika systematycznego i przypadkowego. Wyróżnia się statystykę opisową i statystykę matematyczną.

Pierwsza zajmuje się metodami zbierania i prezentacji informacji statystycznych i ich sumarycznego opisu przy wykorzystaniu takich parametrów, jak miary średnie oraz miary dyspersji. Druga, oparta na rachunku prawdopodobieństwa, umożliwia uogólnienie wyników badań, ocenę stopnia dokładności i wiarygodności wyników. Statystyka znajduje obecnie zastosowanie w wielu naukach, zarówno technicznych, jak i społecznych.

Statystyczne badania, zespół czynności zmierzających do uzyskania, za pomocą metod statystycznych, informacji charakteryzujących zbiorowość objętą badaniem (zbiorowość statystyczną).

Etapami badań statystycznych są:

1) obserwacja statystyczna,

2) opis (statystyczne grupowanie),

3) analiza (statystyczna analiza).

Wyróżnia się badania pełne (obejmujące wszystkie jednostki wchodzące w skład zbiorowości), badania częściowe (nie wyczerpujące, obejmujące tylko część zbiorowości, czyli próbę wybraną w odpowiedni sposób. n.p. badania reprezentacyjne, badania monograficzne, badania ankietowe).

Statystyka społeczno-gospodarcza,

1) dziedzina działalności polegająca: na organizowaniu i przeprowadzaniu statystycznych badań całokształtu zjawisk społeczno-gospodarczych, na analityczno-liczbowym opisie wyników tych badań oraz na formułowaniu wniosków i prognoz.

2) zbiór informacji liczbowych (danych statystycznych) dotyczących masowych zjawisk społeczno-gospodarczych.

Statystyczny wskaźnik( indeks), oznaka, cecha przedmiotu lub zjawiska połączona z pewną inną jego cechą takim stałym związkiem, że wystąpienie jej pozwala statystycznie (bezwyjątkowo) stwierdzić obecność lub przewidzieć zaistnienie tej innej cechy.

W statystyce rozróżnia się trzy zasadnicze statystyczne wskaźniki: natężenia, struktury, dynamiki.

Przez pojęcie "wskaźnik natężenia" rozumiemy stosunek dwóch różnych wielkości pozostających w pewnym związku logicznym, np. stosunek liczby ludności jakiegoś kraju do wielkości jego terytorium. Gdy badanie polega na porównaniu części badanej zbiorowości z całą zbiorowością, posługujemy się wskaźnikami struktury, które określają, jaką część całości stanowią wyróżnione elementy. Wskaźnik dynamiki to stosunek wartości zmiennej zależnej w okresie badanym jej od wartości w okresie podstawowym.

Statystyczny materiał, wyniki obserwacji przeprowadzonej wyłącznie w celach statystycznych (pierwotny statystyczny materiał). Do badań statystycznych wykorzystuje się również wtórny statystyczny materiał, tj. dane zebrane do celów niestatystycznych, np.: karty robocze, listy płac, dane z rachunkowości przedsiębiorstwa, karty zdrowia prowadzone przez lekarzy itp.

Statystyka matematyczna, nauka o budowie reguł wnioskowania o właściwościach badanej zbiorowości statystycznej na podstawie danych dotyczących części tej zbiorowości, wybranej w sposób losowy.

Statystyczne cechy, właściwości, którymi odznaczają się jednostki wchodzące w skład badanej zbiorowości.

STATYSTYCZNA ANALIZA badanie i interpretacja zebranego materiału statystycznego w celu ujawnienia w nim określonych prawidłowości i związków oraz formułowanie na ich podstawie wniosków; obejmuje analizę struktury, dynamiki, natężenia i współzależności.

STATYSTYCZNE BADANIE , opis statystyczny badanie zbiorowości statystycznej, ukierunkowane na opracowanie modelowego wzorca; obejmuje trzy etapy: obserwację (gromadzenie materiałów, przeważnie w postaci szeregu wypełnionych w trakcie badań kwestionariuszy), opis (weryfikacja poprawności obserwacji i klasyfikacja zebranych materiałów) i analizę zarówno jakościową jak ilościową cech określających daną zbiorowość statystyczną; b.s. wyczerpujące obejmuje wszystkie jednostki należące do danej zbiorowości (np. w trakcie nar. spisu powszechnego); b.s. nie wyczerpujące obejmuje tylko część zbiorowości, wyodrębnioną dzięki zastosowaniu metod reprezentacyjnych; w niektórych wypadkach stosuje się ankietę lub metodę monograficzną; aby b.s. nie wyczerpujące dało wyniki, które można przenieść z dużym prawdopodobieństwem na całą zbiorowość, struktura badanej części powinna być jak najbardziej zbliżona do całości (np. analizy popularności polityków przed wyborami, prowadzone w miejscowościach, w których skład społ. mieszkańców można uznać za reprezentatywny dla całej zbiorowości wyborców).

Statystyczne badania, zespół czynności zmierzających do uzyskania, za pomocą metod statystycznych, informacji charakteryzujących zbiorowość objętą badaniem (zbiorowość statystyczną).

Etapami badań statystycznych są:

1) obserwacja statystyczna,

2) opis (statystyczne grupowanie),

3) analiza (statystyczna analiza).

Wyróżnia się badania pełne (obejmujące wszystkie jednostki wchodzące w skład zbiorowości), badania częściowe (nie wyczerpujące, obejmujące tylko część zbiorowości, czyli próbę wybraną w odpowiedni sposób. n.p. badania reprezentacyjne, badania monograficzne, badania ankietowe).

Statystyczna obserwacja, wstępny etap badania statystycznego, którego celem jest zgromadzenie danych o określonym zjawisku, lub ich grupie, za pomocą spisu, rejestracji bieżącej lub statystycznej sprawozdawczości. Może mieć charakter badania pełnego, dotyczącego wszystkich jednostek zbiorowości statystycznej (w takim przypadku nie występuje problem wnioskowania statystycznego, a oceny wyprowadzone z obserwacji odnoszą się do tej samej zbiorowości statystycznej), lub badania reprezentatywnego, dotyczącego niektórych jednostek wybranych ze zbiorowości statystycznej drogą losowania (opis prób losowych jest wówczas początkiem analizy, natomiast wnioskowanie o populacji generalnej stanowi jej zakończenie).

Statystyczna obserwacja jest stwierdzeniem i pisemną rejestracją wielkości, jakie badane cechy przyjmują u poszczególnych jednostek zbiorowości statystycznej.

Statystyczna prawidłowość, powtarzalność, następstwo, porządek zjawisk statystycznych. Przejawia się tylko w procesach masowych, tj. gdy zbiorowości są bardzo liczne, natomiast może być niedostrzegalna w pojedynczych przypadkach. Występowanie statystycznej prawidłowości jest spowodowane kształtowaniem się procesu masowego pod wpływem przyczyn determinujących rozwój zjawisk w określonym kierunku, jak również przyczyn o charakterze losowym, powodującym, że wystąpienie pojedynczego zjawiska jest zdarzeniem losowym. Statystyczna prawidłowość są przejawem działania prawa wielkich liczb.

Statystyczna sprawozdawczość, system obowiązujących sprawozdań statystycznych zawierających dane liczbowe o wynikach osiągniętych w różnych dziedzinach działalności, podawanych w ściśle określony sposób, o zakresie tematycznym i grupowaniach ustalonych w treści poszczególnych formularzy sprawozdawczych.

STATYSTYCZNE SZEREGI rząd wielkości statystycznych uporządkowanych w zależności od celu przyjętego w badaniu statystycznym; sz.s. składa się z dwóch rubryk, z których jedna opisuje treść kolejnych pozycji, zaś druga podaje liczbę jednostek przypadających na daną kategorię przedmiotów, osób lub zjawisk; sz.s. strukturalne przedstawiają strukturę badanej zbiorowości, jej podział jakościowy (np. płeć) i ilościowy (np. rozmaite przedziały wiekowe); sz.s. geograficzne ilustrują rozmieszczenie wielkości statystycznych w przestrzeni (np. liczba bezrobotnych w różnych woj.); sz.s. dynamiczne ilustrują zmiany w liczebności pewnych faktów lub stanów zachodzące w wybranym czasie; sz.s. rozdzielcze tworzy się przez podział badanej zbiorowości na grupy wg pewnej cechy; szeregi opierające się na równych przedziałach (np. liczba bezrobotnych na 1000 mieszk.) są nazywane szeregami rozdzielczymi prostymi; szeregi kumulacyjne powstają przez dodawanie kolejnych przedziałów klasowych i odpowiadających im odpowiednich wartości szeregu rozdzielczego prostego (np. liczba bezrobotnych na 1000 kobiet w wieku 25-35 lat w woj. katowickim w okresie 1989-97); sz.s. rozdzielczy prosty jest podstawowym narzędziem analizy statystycznej

STATYSTYCZNA ZBIOROWOŚĆ wyodrębniony i jednoznacznie określony zbiór przedmiotów, osób lub zjawisk poddanych badaniu statystycznemu; składniki z.s. są podobne do siebie pod względem pewnych cech, zaś pod względem innych - różne, stąd też wyodrębnia się z.s. jednorodne (dominuje podobieństwo elementów) lub niejednorodne (dominują różnice).

Waloryzacja, przywracanie wartości zdeprecjonowanym wierzytelnościom pieniężnym oraz różnorodnym płatnościom w celu ich urealnienia, w związku ze spadkiem siły nabywczej pieniądza, spowodowanym głównie przez inflację. Dotyczy różnego rodzaju składek (np. ubezpieczenia), rent, emerytur, wynagrodzeń itp.

Wartość nominalna, wartość danego dobra, usługi lub innej rzeczy wyrażona najczęściej w pieniądzu i wyznaczana przez ceny bieżące, bez uwzględnienia wpływu innych czynników, np. inflacji.

WARTOŚĆ OCZEKIWANA (wartość średnia, nadzieja matematyczna), mat. dla zmiennej losowej X liczba oznaczana EX: dla X — skokowej, przyjmującej wartości x₁, x₂, ... z prawdopodobieństwami odpowiednio p₁, p₂, ..., EX= x₁p₁ + x₂p₂ + ... ; dla X — ciągłej, o gęstości f (x),
x f (x)dx.

Wartość realna, wartość danego dobra, usługi lub innej rzeczy wyrażona najczęściej w pieniądzu, wyznaczona przez ceny i uwzględniająca wpływ czynników zewnętrznych, np. inflacji.

Zaktualizowana wartość, wartość teraźniejsza, aktualna wartość przepływów pieniężnych (dochodów, wydatków) lub kapitału, które zaistniały w przeszłości lub powstaną w przyszłości.

Zaktualizowana wartość przyszłych wielkości ekonomicznych oblicza się przez dyskontowanie (dyskonto) ich oczekiwanej, przewidywanej wartości, za pomocą przyjętej stopy dyskontowej. Do obliczenia zaktualizowanej wartości wielkości ekonomicznych z przeszłości stosuje się procent składany.

Zaktualizowana wartość znajduje zastosowanie m.in. w: obrocie papierami wartościowymi, ocenie efektywności inwestycji oraz wycenie przedsiębiorstw i nieruchomości.

Zbiorowość statystyczna, jednoznacznie określony i wyodrębniony zbiór jednostek (np. osób, przedmiotów, zjawisk) poddanych badaniu statystycznemu.

Jednostki te mają jedną lub kilka cech wspólnych (są to cechy statystyczne, podlegające badaniu), ale są zróżnicowane pod względem ich wartości i jakości, a także pod względem innych posiadanych cech.

ZADANIA, PROBLEMY ,TESTY

Zadania

Które z podanych niżej zbiorów tworzą szereg czasowy, a które mają charakter danych przekrojowych?

a Wydatki ludności na trwałe dobra konsumpcyjne w latach 1980-- 1991.

b Wydatki gospodarstw domowych na utrzymanie mieszkań w 1990 r.

c Miesięczny wskaźnik cen ziemnia­ków w 1990 r.

d Produkt narodowy brutto Wielkiej Brytanii w poszczególnych kwarta­łach 1991 r.

e Przeciętne tygodniowe zarobki wy­branej grupy 350 osób, badanej w la­tach: 198, 1984, 1986 i 1988.

f Bezrobocie w poszczególnych gałę­ziach według miejsca ostatniego za­trudnienia w dniu 10 maja 1987 r.

Odpowiedź

Zbiory danych a, c i d zawierają infor­macje dotyczące tych samych zmien­nych w różnych okresach; tworzą więc szeregi czasowe. Zbiory b i f to dane przekrojowe, dotyczą bowiem różnych jednostek lub ich grup w tym samym okresie. W punkcie e mamy jeszcze inny zestaw danych. Są to dane prze­krojowe powtarzane w różnych okre­sach. Łączą one cechy szeregów czaso­wych i danych przekrojowych. Niekie­dy określane są jako dane panelowe Spotyka się je rzadko, ponieważ ich zbieranie jest kosztowne i trudne ze względu na konieczność ankietowania tych samych osób w różnych okresach

Zadanie

Tablica Zatrudnienie w rolnictwie

w wybranych krajach Europy Zachodniej (w tys..)

Kraje 1976 1989 Wskaźnik (1976= 100)

Kraje	1976	1989
Belgia	128	103
Dania	191	154
RFN	803	702
Francja	2082	1576
Holandia	261	248
Wielka Brytania	685	603

Tablica przedstawia dane dotyczące wielkości zatrudnienia w rolnictwie w sześciu krajach Europy Zachodniej w latach 1976 i 1986

a Na podstawie danych (nie korzys­tając z kalkulatora) scharakteryzuj tendencję rozwojową zatrudnienia w rolnictwie. W których krajach ten­dencja ta zaznaczyła się najmocniej, a w których najsłabiej?

b Dla każdego kraju oblicz wskaźnik zatrudnienia w 1986 r., przyjmując 1976 = 100.

e Po obliczeniu wskaźników sprawdź odpowiedź na pytanie a. Czy prawid­łowo wskazałeś kraje o najbardziej i najmniej wyraźnym trendzie

Odpowiedź

a Prosta analiza liczb niewiele nam powie. Z danych wynika, że poziom zatrudnienia w rolnictwie w rozpa­trywanym dziesięcioleciu obniżył się we wszystkich krajach, ale absolutne rozmiary tego zatrudnienia są nader zróżnicowane. W liczbach bezwzględnych bardzo duży spadek zatrudnie­nia zanotowano w rolnictwie francu­skim. Aby jednak ocenić, o ile pro­cent zmalało zatrudnienie, musimy wykonać pewne obliczenia.

b obliczenia zawarte są w poniższej tablicy

.

Kraje	1976		1989 Wskaźnik (1976= 100)
Belgia	128		103 80,5
Dania	191		154 80,6
RFN	803		702 87,4
Francja	2082		1576 73,8
Holandia	261		248 95,0
Wielka Brytania	685		603 88,0

e Wskaźniki procentowe ułatwiają po­równanie sytuacji w różnych krajach. Okazuje się, że największy spadek zatrudnienia w rolnictwie nastąpił we Francji o - 26,2%, a najmniejszy w Holandii ­o - 5 %.

PYTANIA i ZADANIA

1). Narysuj kilka wykresów pokazujących:

a) dwie zmienne rosnące i malejące razem

b) dwie wielkości, które zmieniaj się w przeciwnym kierunku

c) zależność między zmiennymi osiągając maksimum

d) zależność między zmiennymi osiągającą minimum

2): Która z zależności z pytania 1 jest dodatnia, a która ujemna?

3). Jak brzmi definicja nachylenia wykresu zależności między zmiennymi?

4). Jakie są dwa sposoby obliczania nachylenia krzywej?

5). W jaki sposób wykreślamy zależność między więcej niż dwoma zmiennymi?

6) Wykorzystaj poniższe informacje do wykreślenia zależności między X i Y

X 0 1 2 3 4 5 6 7 8

Y 0 1 4 9 16 25 36 49 64

a) Czy zależność ta jest dodatnia, czy ujemna?

b) Czy nachylenie krzywej rośnie, czy maleje wraz ze wzrostem X?

7.Oblicz nachylenie krzywych wykreślonych dla poniższych zależności

1. X 0 2 4 6 8 10

Y 20 16 12 8 4 0

b) X 0 2 4 6 8 10

Y 0 8 16 24 32 40

8). Narysuj wykres dla poniższej zależności­

X 0 1 2 3 4 5 6 7 8 9

Y 0 2 4 6 8 10 8 6 4 2

1. Czy nachylenie jest dodatnie, czy ujemne dla X= 5

2. Czy nachylenie jest stale czy zmienna

3. Jakie jest nachylenie krzywej dla X=8

4. Czy Y osiąga maksimum czy minimum dla X = 5

9). Narysuj wykres dla poniższej zależności

X 0 1 2 3 4 5 6 7 8 9

Y 10 8 6 4 2 0 2 4 6 8

1. Czy nachylenie jest dodatnie, czy ujemne dla X= 5

2. Czy nachylenie jest dodatnie, czy ujemne dla x 5:

5. Jakie jest nachylenie krzywej dla x = 5''

6. Czy Y osiąga maksimum czy minimum dla X = 5

10). Jeśli zależność między X i Y jest dodatnia, to dużym wartościom Y odpowiada:

1. X = 0

2. X małe

3. X duże

4. X dodatnie

e) X*Y

11). Jeśli krzywa przechodzi przez punkty (3,8), (5,13), to nachylenie wynosi:

a) 5

b) 2,5

c) 2

d) 0,4

e) 0,2

12). Nachylenie linii poziomej

1. równa się jeden

2. jest dodatnie

3. równa się zero

4. jest nieokreślone, gdyż nie można dzielić przez zero

4. jest większe od jednego

13). Jeżeli krzywa osiąga swoje maksimum w punkcie (5,10), to jej nachylenie w tym punkcie jest

1. 10:5 =2

2. większe od 2 ...

3. ujemne

4. niemożliwe do określenia z podanych informacji 3b

5. równe zero

14) Nachylenie krzywej między punktami a (10,5) i b (20,10) wynosi

1. 0,5

2. 1,0

3. 1,5

d) 2,0

15 , Jeżeli nachylenie krzywej równa się zera, to

1. osiąga ona minimum

2. osiąga ona maksimum

3. znajduje się ona w punkcie (0 , 0)

4. posiada ona maksimum lub minimum

5. wszystkie odpowiedzi są dobre

16 Krzywa pokazująca zależność X i Y ma nachylenie równe -2 w każdym punkcie. Wykreśl tę linię, a następnie drugą wypukłą i styczną do niej. Jakie jest nachylenie wypukłej krzywej w punkcie styczności.

17. Równanie jest sposobem użycia algebry dla wyrażenia zależności między zmiennymi. Następujące równania opisuje relacje między ceną butów sportowych a ich ilościami.

Ilość jaką chcą kupić konsumenci: Qd = 300 - 3C

Ilość jaką chcą sprzedać producenci: Qs = 2C

gdzie C jest ceną za parę butów.

Narysuj wykres obu równań, używając następujących wartości dla

C : 30, 40, 50, 60, 70, 80, np.. tys.. zł.

Wyznacz wartość C , dla jakiej przetną się obie krzywe, i wskaż odpowiednie ilości butów jakie zostaną kupione i sprzedane.

Zadanie

Na rysunku poniżej pokazane są wykresy punktowe czterech rodzajów zależności między parami zmiennych.

Rys a Rysa b Rys. c Rys. d

* * ** *

* * * *

* * * * * *

* * * * * *

* * * * * *

*

I ujemna zależność liniowa , II - dodatnia zależność liniowa, III --- zależność nieliniowa, IV brak możliwości określenia zależności

Każdemu wykresów przyporządkuj odpowiadający mu opis: Na którym z powyższych wykresów na pewno nie spróbujesz wykreślić linii prostej?

Odpowiedź (a) -II; (b)-III ; (c)--1V: (d)-- I. Linia prosta nie odpowiada rozkładowi punktów na wykresie (b) i ((c).

Zadanie

Wskaźniki cen detalicznych odzieży i obuwia w Wielkiej Brytanii W latach 1983 - 1986 kształtował się: następująco ( 15 1 1974 = 100):

Lata 1983 1984 I985 1986

Wskaźnik 214,8 214,6 222,9 229,2.

a. Jakich dodatkowych informacji po­trzebujesz dla sprawdzenia, czy in­deks cen realnych odzieży i obuwia obniżył się lub wzrósł w badanym okresie ?

b. Oblicz wskaźnik cen realnych odzie­ży i obuwia, wykorzystując obliczony w zadaniu 4 zagregowany indeks cen który wynosił

c. Objaśnij uzyskane wyniki.

Odpowiedzi

a Do porównania dynamiki cm niezbędny ,jest ogólny indeks cen: potrzebujemy informacji na temat kształtowania się cen odzieży i obu­wia w stosunku do cen innych dóbr.

b Indeks cen realnych odzieży i obuwia:

1983 1984 1985 1986

64,1 61,0 59,7 59,4

Sposób obliczenia:

Indeks cen odzieży i obuwia

Wartość indeksu w 1983 r.=------------------------------- ----------* 100

ogólny indeks cen

c. Ceny odzieży i obuwia rosły znacznie wolniej niż ceny pozostałych dóbr, dlatego realne ceny odzieży i obuwia od 1974 r. wykazują tendencję zniż­kową.

Zadanie

Pamiętasz rozważania o wartościach realnych i nominalnych danej sumy pieniądza z rozdziału Warsztat ekonomisty ? Otóż w 1997 r. tempo inflacji było równe 18%.

1. Ile pod koniec 1997 r. wynosiła realna wartość stałej nominalnej kwoty pieniądza z początku 1997 r równa 1000zł .? (Jako miary użyj jednostki pieniężnej o sile nabywczej z początku 1997r.)

2. Czy to prawda , że realna wartość stałego dochodu nominalnego zmniejszyła się 1997 r. o 18%? Odpowiedź uzasadnij.

Rozwiązanie

1. W końcu 1997 r. szukana realna wartość stałej nominalnej kwoty pieniądza wynosiła

1000 1000

------------= --------------= 847 zł

(1+18%). 1,18

2. Skoro tak, to zmiana absolutna realnej kwoty tej kwoty wynosiła:

1000- 847=153

a zatem procentowa zmiana wynosiła

153/1000=0,153* 100= 15,3%

ten sam wynik otrzymamy

847/1000=0,847* 100 = 84,7 - 100=-15,3%

A zatem, w ujęciu procentowym realna wartość zmniejszyła się o mniej niż 18%

Zadanie

Koszty utrzymania mieszkania wynoszą 20% ogólnej sumy wy­datków. O ile spadły dochody realne ludności, jeśli płace nomi­nalne nie zmieniły się, zaś koszty utrzymania mieszkania wzro­sły o 15% w ciągu roku. (Odp.:.: spadły o 3%.)

100*0,8+115*0,2=80+23=103-100=3%

Zadanie

W jakim przy­padku dochody realne spadłyby w takim samym stopniu, jak wzrost kosztów utrzymania mieszkania, tzn.. o 15%. (Odp..: gdy­by wszystkie dochody ludzie wydawali tylko i wyłącznie na utrzymanie mieszka­nia.)

Zadanie

Płaca nominalna wzrosła z 500 do 600 zł, zaś w tym samym czasie wskaźnik wzrostu cen wynosił 130. Oblicz jak zmieni­ła się płaca realna?

(Odp.:.: spadła o 7, 8%.)

Płaca realna 600:130=461

Spadek płacy realnej w wartościach absolutnych 461-500 =-39

Tempo spadku płacy realnej 39: 500* 100 =-7,8%

Zadanie

Płaca nominalna wzrosła z 500 do 600 zł, zaś w tym samym czasie wskaźnik wzrostu cen wynosił 130.

Koszty utrzymania mieszkania wynoszą 20% ogólnej sumy wy­datków. O ile spadły dochody realne ludności, jeśli płace nomi­nalne nie zmieniły się, zaś koszty utrzymania mieszkania wzro­sły o 15% w ciągu roku.

(Odp.:.: spadły o 3%.)

W jakim przy­padku dochody realne spadłyby w takim samym stopniu, jak wzrost kosztów utrzymania mieszkania, tzn.. o 15%.

(Odp..: gdy­by wszystkie dochody ludzie wydawali na utrzymanie mieszka­nia.)

Zadanie

Przypuśćmy, że wydatki na żywność stanowią 40% ogółu wydatków ludności, a 60% stanowią wydatki na inne towary i usługi. Wskaźniki cen w tych dwóch grupach wydatków w 1997 r. kształtowały się następująco (1996 = 100):

Wyszczególnienie 1997

Żywność 113

Inne towary i usługi 116

Ogólny wskaźnik cen towarów i usług konsumpcyjnych (wskaźnik cen detalicznych) obliczymy w następujący sposób:

0,4*113-++ 0,6*116 45,2 +69,6

-----------------------= ---------------= 114,8.

0,4 + 0,6 1

Średnio biorąc, ceny towarów i usług konsumpcyjnych wzrosły o 114,8 -100 = 15%.

Zadanie

Informacje zawarte w poniższej tablicy stano­wią elementy wskaźnika cen detalicz­nych w Wielkiej Brytanii w 1990 r. w stosunku do roku 1985

Tablica Wskaźniki cen detalicznych w Wielkiej Brytanii w 1990 r.

Rodzaj wydatków	Wagi Indeksy
Żywność	0,3 170
Mieszkanie, c.o., gaz i światło	0, 2 186
Pozostałe dobra i usługi	0,5 173

Która z podanych liczb wyraża wartość ogólnego wskaźnika cen detalicznych

172; 173; 174.7; 176,3 ; 178

Przeprowadź obliczenia.

Obliczenia:

3 * 170 + 2 * 186 + 5 * 173 = 1747.

Liczbę tę musimy podzielić przez sumę wag (2 + 3 + 5 = 10), co daje 174,7.

Inny sposób obliczenie przy wykorzystaniu wskaźników cząstkowych

0,3*170+0,2*186+0,5*173 51+37,4+86,5

----------------------------------- =------------------------= 174,9

0,3+0,2+0,5 1

Zadanie

Tablica informuje o cząstkowych indeksach cen detalicznych i o udziałach wydatków gospodarstw domowych na główne grupy dóbr konsumpcyjnych w ca*o*ci wydatków w Polsce w 1996 r. (1995 = 100).

	Żywność	Napoje alkoholowe	Towary nieżywnościowe	Usługi
Indeksy	118,6	125,4	120,7	120,1
Udziały	39,6%	4,2%	29,8%	26,4%

1. Z agregowany indeks cen detalicznych wynosił

2. Stopa inflacji w Polsce w 1996 r. wynosiła ?

3. Stopa inflacji dla abstynent*w, którzy nie kupuj* napojów alkoholowych, lecz w zamian za to odpowiednio więcej usług

Problemy sprawdzające

Zadanie

Wykorzystując dane z tablicy, skonstruuj wykres punktowy ilust­rujący zależność między wskaźnikiem tygodniowej płacy a wskaźnikiem cen detalicznych.

Stawki płac nominalnych i realnych w przemyśle przetwórczym w latach 1971-1983
	1971	1973	1975	1977	1979	1981	1983
Wskaźnik płac nominalnych	100	128,3	195,3	145,1	333,1	427,0	476,7
Wskaźnik cen detalicznych	100	117,0	168,6	227,6	279,6	384,3	419,4
Wskaźnik plac realnych	100	109,7	115,6	107,8	119,0	111,2	114,0

2. Poniższa tablica przedstawia całkowitą konsumpcję (wydatki gospodarstw domowych) i całkowity dochód gospodarstw domowych w Wielkiej Brytanii. Obie wielkości są wyrażone w milionach funtów w cenach 1980 r.:

	1979	11980	1981	1982	1983	1984	1985
Dochód	159,1	161,2	157,3	157,9	161,6	165,8	169,4
Spożycie	137,6	137,0	136,6	137,6	142,9	145,6	149,7

a) narysuj wykres punktowy, na którym na osi pionowej zaznaczona jest konsumpcja, a na osi poziomej dochód;

b) wykreśl linię dopasowaną do wszystkich punktów na wykresie;

c) czy możesz wykorzystać tę linię do przedstawienia zależności między kon­sumpcją a dochodem i czy twoja interpretacja ma sens?

3. Wykorzystując dane z poniższej tabeli

	1975	1976	1977	1978	1979	1980	1981
Y X	40 5	33 7	29 9	5fi 3	81 1	19 11	20 10

a Narysuj wykres punktowy przedstawiający zmienną X wyrażoną w złotówkach i mierzoną na osi pionowej oraz zmienną Y wyrażoną w tonach i mierzoną na osi poziomej:

b. czy zależność między zmiennymi jest dodatnia czy ujemna,

c. czy linia prosta czy też krzywa jest lepiej dopasowana do rozrzuconych na wykresie punktów?

4. Zostałeś zatrudniony przez policję w departamencie studiów do zbadania, czy istnieje związek między liczbą przestępstw kryminalnych a wielkością bezrobocia: a) w jaki sposób zweryfikujesz tę hipotezę; jakich danych potrzebujesz; b) jakie czynniki przyjmiesz za stałe?

5. Na podstawie danych tam zamieszczonych tabeli

Stawki płac nominalnych i realnych w przemyśle przetwórczym w latach 1971-1983
	1971	1973	1975	1977	1979	1981	1983
Wskaźnik płac nominalnych	100	128,3	195,3	145,1	333,1	427,0	476,7
Wskaźnik cen detalicznych	100	117,0	168,6	227,6	279,6	384,3	419,4
Wskaźnik plac realnych	100	109,7	115,6	107,8	119,0	111,2	114,0

1. skonstruuj wskaźnik tygodniowej płacy (pracowników fizycznych), przyj­mując 1975 = 100.

2. oblicz wskaźnik cen detalicznych przy 1975 = 100. Następnie oblicz wskaźnik płac realnych przy 1975 = 100. O ile procent wzrosły płace realne w latach 1971-1973?

3. Czy otrzymałbyś te same odpowiedzi, wykorzystując bezpośrednio wskaźniki zamieszczone

6. Poniższa tablica zawiera wskaźnik cen detalicznych oraz wskaźnik cen energii, ilustrujący zmiany cen węgla, gazu, elektryczności, ropy naftowej i oleju:

	11971	1973	1975	1977	1979	1981	1983	1985
Wskaźnik cen detalicznych	100	115,7	166,7	223,8	276,5	366,3	416,1	463,3
Wskaźnik cen energii	100	110,8	172,8	248,3	293,6	445,4

1. oblicz wskaźnik realnych cen energii (1971 = 100);

2. odkładając poszczególne lata na osi poziomej, zaznacz trzy szeregi czasowe: wskaź­nik cen detalicznych, wskaźnik cen energii i wskaźnik realnych cen energii;

3. jakie są według ciebie przyczyny takiego właśnie zachowania się cen energii;

4. na rysunku 2.9 pokazano, w jaki sposób zmiany realnych cen biletów autobusowych mogą wpływać na zależność między cenami biletów na przejazd metrem a przychodami z usług metra; wiadomo, że ceny energii wpływają na koszty jazdy prywatnymi środ­kami lokomocji; czy zmiany realnych cen energii prowadzą do wzmoc­nienia czy osłabienia wpływu zmian realnych cen biletów autobusowych na zależność między cenami biletów na przejazd metrem a sumą przychodów z eksploatacji metra?

Odpowiedz Tak / Nie

1 Ekonomia nie jest nauką ścisłą, ponieważ nie może opierać się na doświadczeniach przeprowa­dzanych w laboratoriach.

Nie. To prawda, że ekonomiści nie prowadzą eksperymentów w labo­ratoriach'°, ale stosują naukowe metody do rozwiązywania proble­mów ekonomicznych i wykorzys­tują w możliwie najlepszy sposób dostępne informacje. Istnieją także inne nauki nieeksperymentalne, jak astronomia, niektóre działy biolo­gii itd.

2 Możemy zgromadzić do­wody potwierdzające daną teorię, ale nigdy z całą pewnością nie mo­żemy dowieść, że jest ona słuszna. Tak (zob. podrozdział 2.9 podręcz­nika).

3 Wykresy dobrze uwydat­niają charakterystyczne cechy sze­regów czasowych.

Tak. Przy sporządzaniu wykresu należy uważać, aby nie zniekształ­cić rzeczywistego obrazu.

4 Jeżeli między dwiema zmiennymi istnieje ścisły związek statystyczny, to istnieje między nimi zależność przyczynowo-skutkowa.

Nie. Związek statystyczny może być przypadkowy - niekiedy obie zmienne są zależne od trzeciej zmiennej lub obie rosną niezależ­nie.

5 Dane przekrojowe są czę­ściej wykorzystywane w mikroeko­nomii, gdyż dotyczą na ogół za­chowań poszczególnych jednostek. . Tak, ale nie jest to regułą.

6 Zakładając, że „pozosta­łe" czynniki są stałe, możemy po­minąć bardziej skomplikowane ele­menty modelu ekonomicznego. Nie. Założenie „pozostałe czynniki stałe" umożliwia uproszczenie ana­lizy i skoncentrowanie się. na wy­branych fragmentach modelu. Nie­mniej nie możemy ignorować tych „pozostałych czynników", ponie­waż wpływają one na położenie poszczególnych krzywych, które badamy w naszej analizie".

7 Model ekonomiczny dotyczy liniowej zależności między badanymi zmiennymi. Nie. Dla uproszczenia analizy za­kładamy często występowanie funkcji liniowej, ale w wielu zależ­nościach ekonomicznych relacja między zmiennymi ma charakter nieliniowy.

8 Jeżeli poświęcisz dużo uwagi obserwacji faktów, to z pew­nością odkryjesz prawidłową teorię. Nie. Fakty nie wystarczą do sfor­mułowania teorii. Ich interpretacja wymaga logicznego myślenia.

9 Indeksy są niezbędnym narzędziem porównywania zmien­nych mierzonych w różnych jedno­stkach. Tak. Są, oczywiście, również inne zastosowania indeksów.

10 Dodatnia korelacja mię­dzy zmiennymi świadczy o prawid­łowości naszego modelu. Nie. Dodatnia korelacja wskazuje tylko kierunek zależności między dwiema zmiennymi.

11 Wskaźnik cen detalicznych, pozwalający mierzyć koszty utrzy­mania, obliczamy jako średnią wa­żoną cen poszczególnych dóbr. Tak.

12 Inflacja jest mierzona po­ziomem cen. Nie. Inflację mierzymy stopą zmian poziomu cen.

13 Płacę realną obliczamy pomniejszając płacę nominalną o zmiany w kosztach utrzymania. Tak.

14 Empiryczne badania su­gerują, że na ogół podwyżkom cen biletów metra towarzyszy spa­dek liczby przewożonych pasa­żerów. Tak. Porównaj dyskusję i argu­menty przedstawione w rozdziale 2 podręcznika, szczególnie w pod­rozdziale 2.6 i 2.8.

Pojęcia i określenia

Każdemu z pojęć oznaczonych literami przyporządkuj odpowiednie określenie oznaczone liczbą:

(a) dane statystyczne

(b) stopa wzrostu

(c) wskaźnik (indeks)

(d) model ekonomiczny

(e) funkcja

(f) zmienna nominalna

(g) siła nabywcza pieniądza (h) cena realna

(i) szereg czasowy

(j) zależność dodatnia

(k) wskaźnik cen detalicznych

(1) ceteris paribus (przy pozosta­łych czynnikach niezmiennych) m) dane przekrojowe

(n) wykres punktowy (o) ekonometria

(p) zależność ujemna

(q) wskaźnik produkcji przemysłowej

(r) zmienna realna

1. Szereg kolejnych wartości imiennej w różnych okresach.

2. Sytuacja, w której wyższym warto­ściom danej zmiennej towarzyszą niższe wartości innej zmiennej.

3. Cena danego dobra odniesiona do ogólnego poziomu cen.

4. Założenie upraszczające, które umożliwia skoncentrowanie się na podstawowych zależnościach.

5. Świadomie uproszczony obraz rze­czywistości, oparty na szeregu upraszczających założeń, przydat­ny do analizy zachowań ludzi w ży­ciu gospodarczym (oraz związków zachodzących między zjawiskami i zmiennymi ekonomicznymi).

6. Wskaźnik cen dóbr nabywanych przez typowe gospodarstwo do­mowe.

7. Zmienna mierzona w jednostkach pieniężnych w cenach bieżących.

8. Procentowa zmiana danej wielko­ści w jakimś okresie (na ogół jed­nego roku).

9. Wartości, które przyjmuje dana zmienna w danym punkcie czasowym dla różnych jednostek lub ich grup.

10. Ilość dóbr, które można nabyć za określoną jednostkę pieniężną.

11. Sposób wyrażenia danej wielkości w relacji do jakiejś wielkości pod­stawowej.

12. Wykres ilustrujący relację dwóch zmiennych za pomocą punktów odpowiadających ich wartościom.

13. Sytuacja, w której wyższym warto­ściom jednej zmiennej towarzyszą wyższe wartości drugiej zmiennej.

14. Informacje liczbowe dotyczące kształtowania się poszczególnych zmiennych ekonomicznych.

15. Relacja między zmiennymi ekono­micznymi, w której dana zmienna zależy od jednej lub wielu innych zmiennych, co wyrażamy w formie zapisu: y = f(...).

16. Średnia ważona ilości dóbr produ­kowanych przez przemysł (odnie­siona do wartości z pewnego okre­su wyjściowego, przyjętej za 100).

17. Zmienna mierzona w cenach sta­łych.

18. Gałąź ekonomii zajmująca się mie­rzeniem związków między wielkoś­ciami ekonomicznymi przy wyko­rzystaniu danych statystycznych.

TEST

1. Funkcja ze stałym przyrostem

1. ma stałe nachylenie

2. ma nachylenie rosnące

3. ma nachylenie malejące

4. ma nachylenie ujemne

5. żadne z powyższych

2. Funkcja ze stałym przyrostem.

1. ma stałe nachylenie

2. ma nachylenie rosnące

3. ma nachylenie malejące

4. ma nachylenie ujemne

5. żadne z powyższych

3. Funkcja ze zmiennym przyrostem

1. ma nachylenie dodatnie

2. ma nachylenie ujemne

3. ma nachylenie rosnące

4. ma nachylenie stałe

5. żadne z powyższych

4. Nachylenie linii poziomej

1. jest równe jedności

2. jest równe zero

3. jest dodatnie

4. jest równe nieskończoności

5. żadna z powyższych

	udział	Indeks 1990	Indeks 1995
żywność	40%	100	140
pozostałe	60%	100	125
dochód nominalny	1 000	1500

5. Ustal ile wynosi wskaźnik wzrostu cen

a) 120 b) 140 c) 130 d) 131

6. Ustal ile wynosi tempo wzrostu dochodu nominalnego

a) 20% b) 30% c) 40% d)50%

7. Ustal ile wynosi dochód realny w 1995 r.

a) 1000 b) 1500 c) 1145 d) 1200

8. Ustal tempo wzrostu dochodu realnego

a) 19% b)20% c) 14,5% d)50%

Test

1. Wykres punktowy:

/A/ Umożliwia porównanie kierunku zmian obu zmiennych.

/B/ Może zosta* wykonany tylko w przypadku zależności liniowej zmiennych.

/C/ Może zosta* wykonany tylko wtedy, gdy jedna zmienna nie jest przyczyn* zmian drugiej zmiennej.

/D/ Umożliwia ustalenie kierunku zależności przyczynowej obu zmiennych.

(E) Wszystkie dobre

2. Wskaż odpowiedzi, które zawieraj* ca** prawd* i tylko prawd*. Cena mas*a wzrosła z 80 zł do 100 zł. W tej sytuacji:

/A/ Wskaźnik wzrostu ceny mas*a wynosi 120.

/B/ Stopa wzrostu ceny równa się 20%.

/C/ Cena wzrosła o 1/4.

/D/ Cena zwiększyła się o 20 punkt*w procentowych.

(E) Żadna

3. Wskaźniki (indeksy):

/A/ Pomniejszone o 100 daj* wyra*on* w procentach stop* zmiany zmiennej pomiędzy okresem bazowym, a okresem, którego dotycz*.

/B/ S*u** do opisu tempa zmian zmiennych ekonomicznych.

/C/ Pozostają w takim stosunku do 100 jak zmienna z okresu bazowego do zmiennej z okresu, dla którego obliczamy wskaźnik

/D/ S*u** do opisu struktury gospodarki.

(E) wszystkie dobre

4. Wskaźnik cen detalicznych:

/A/ Jest *średnią arytmetyczną wskaźników zmiany cen głównych grup towar*w nabywanych przez gospodarstwa domowe. t

/B/ Precyzyjnie informuje o zmianach cen wszystkich dóbr wytwarzanych w gospodarce.

/C/ Informuje o zmianach koszt*w utrzymania ludno*ci.

/D/ Nie zmienia się pod wpływem zmiany struktury wydatków gospodarstw

(E) Wszystkie dobre

9. Funkcja ze stałym przyrostem

1. ma stałe nachylenie

2. ma nachylenie rosnące

3. ma nachylenie malejące

4. ma nachylenie ujemne

5. żadne z powyższych

• Funkcja ze stałym przyrostem

1. ma stałe nachylenie

2. ma nachylenie rosnące

3. ma nachylenie malejące

4. ma nachylenie ujemne

5. żadne z powyższych

• Funkcja ze zmiennym przyrostem

6. ma nachylenie dodatnie

7. ma nachylenie ujemne

8. ma nachylenie rosnące

9. ma nachylenie stałe

10. żadne z powyższych

• Nachylenie linii poziomej

6. jest równe jedności

7. jest równe zero

8. jest dodatnie

jest równe nieskończoności

9. żadna z powyższych

	udział	Indeks 1990	Indeks 1995
żywność	40%	100	140
pozostałe	60%	100	125
dochód nominalny	1000	1500

• Ustal ile wynosi wskaźnik wzrostu cen

a) 120 b) 140 c) 130 d) 131

• Ustal ile wynosi tempo wzrostu dochodu nominalnego

a) 20% b) 30% c) 40% d)50%

• Ustal ile wynosi dochód realny w 1995 r.

a) 1000 b) 1500 c) 1145 d) 1200

• Ustal tempo wzrostu dochodu realnego

a) 19% b)20% c) 14,5% d)50%




MATERIAŁY FAKULTATYWNE

STATYSTYKA:

Statystyka nie jest straszna 2004-09-20 15:30:36.
NBPortal

W 1789 roku przeprowadzono pierwszy w Polsce spis powszechny. Rozbiory i wojny sprawiały, że rzadko takie spisy odbywały się w regularnych odstępach. Ale, mimo to, rozwój statystyki w naszym kraju nie odbiegał od europejskich trendów.

- "Nakazujemy, aby wszystkich miast, miasteczek i wsiów królewskich, także naszych stołowych, oraz duchownych i ziemskich, tak dawnych, jako nowo osadzonych i  przybyłych, dziedzice, possessorowie, lub dyspozytorowie, w a co do naszych dóbr stołowych vice-administratorowie, w miastach zaś wolnych królewskich magistraty wielość kominów, nie wyłączając żadnego w Koronie komina, czyli dymu, i równie w Wielkim Xięstwie Litewskim (...) przed komissyami powiatowymi zaprzysięgli" - głosił wstęp do ustawy o powszechnym spisie dymów w Rzeczpospolitej, przyjętej przez Sejm w 1789 roku, czyli jeszcze przed rozbiorami. Dlaczego Sejm tak interesowały akurat kominy czy dymy? Bynajmniej nie z powodu ekologicznej postawy posłów - w tym czasie przyjmowano po prostu, że kto ma dom, posiada i piec lub palenisko. Od kominów więc, a w przypadku "kurnych chat" - od dymów, płaciło się podatek.

Rozbiory nie przerwały rozwoju statystyki na ziemiach polskich. W 1809 roku "statysta" (polityk) Stanisław Staszic wydaje rozprawę "O statystyce Polski. Krótki rzut wiadomości potrzebnych tym, którzy ten kraj chcą oswobodzić, i tym, którzy w nim chcą rządzić". Pierwsze rzeczywiście powszechne spisy ludności (a nie "dymów") przeprowadzono w Księstwie Warszawskim w latach 1808 - 1810. Dla opracowania wyników ankiet powołano jedno z pierwszych w Europie Biuro Statystyczne. W 1811 w Szkole Prawa i Administracji powstała pierwsza Katedra Statystyki. 

W 1827 roku wydano pierwowzory roczników statystycznych: w Warszawie pod tytułem "Tabela Miast i Wsi Królestwa Polskiego". W publikacji podano liczbę domów i ludności dla każdej miejscowości, a w Poznaniu "Atlas Statystyczny Polski i krajów okolicznych". Statystyka rozwijała się szybko na terenach zaboru pruskiego, o czym świadczą regularne spisy ludności, powtarzane co 3 lub 5 lat, od 1840 roku aż do pierwszej wojny światowej. Na terenach przyłączonych do Imperium Rosyjskiego jedyny taki spis przeprowadzono w 1897 roku. 

Polscy statystycy powołali w 1912 roku Polskie Towarzystwo Statystyczne z siedzibą w Krakowie. Pierwszym osiągnięciem tego instytutu było wydanie w 1915 rocznika statystyczno - historycznego pod tytułem "Statystyka Polski". Dzieło to pozostaje do dziś cennym źródłem dla historyków. W 1816 roku ukazał się także "Statystyczny atlas Polski", opracowany przez słynnego kartografa Eugeniusz Romera. 

Zupełnie nowe możliwości dla statystyki stworzyły dopiero niepodległość i zjednoczenie Polski. Jeszcze przed formalnym powstaniem II Rzeczpospolitej, 13 lipca 1918 roku, powstał  Główny Urząd Statystyczny, czyli dobrze znany GUS. Pierwszy w niepodległej Polsce spis powszechny odbył się w 1921 roku. Planowano powtarzać go co dziesięć lat. Następny odbył się zgodnie z planem w 1931 roku, kolejny uniemożliwiła II wojna światowa. 1. marca 1943 okupanci przeprowadzili sumaryczny spis ludności w Generalnym Gubernatorstwie. 

Pierwszy po wojnie rocznik statystyczny został wydany w 1947 roku, pierwszy narodowy spis powszechny przeprowadzono w 1950 r. Od tej pory narodowe spisy przeprowadzano regularnie, w: 1960, 1970, 1878 i 1988. Ostatni, z pewnym opóźnieniem, odbył się w 2002 roku. Roczniki statystyczne ukazują się raz do roku. 

Nowe wymagania dla polskiej statystyki wprowadziła integracja z Unią Europejską. Na kilka lat przed faktyczną akcesją, jeszcze w lipcu 1998 roku, w Brukseli przeprowadzono rozmowy Polski z Unią Europejską na temat przeglądu prawa wspólnotowego w obszarze negocjacyjnym "Statystyka" (tzw. screening). Znacznie wcześniej, bo w 1990 roku Główny Urząd Statystyki nawiązał współpracę ze swoim unijnym odpowiednikiem - Eurostatem.

Obecnie Główny Urząd Statystyczny jest wielką machiną gromadzącą, przetwarzającą i opracowującą morze liczb. GUS, poza regularną publikacją całego szeregu danych i wskaźników, przedstawia także wiele raportów dotyczących wybranych dziedzin naszego życia.  

źródło: opracowano na podstawie danych GUS

GUS czyli życie w liczbach 2004-09-20 12:00:00.0


Media bardzo często powołują się na dane statystyczne, w tym te zbierane i opracowywane przez Główny Urząd Statystyczny. Czy wiecie Państwo, że np. pierwszy ogólnokrajowy spis powszechny miał miejsce ponad dwieście lat temu?


Statystyka przy pomocy danych liczbowych opisuje wszystkie najważniejsze dziedziny naszego życia. Z informacjami statystycznymi spotykamy się codziennie w mediach - w relacjach telewizyjnych, gazetach, itp. Dzięki statystyce, wiemy, jak żyje przeciętny obywatel, czyli dowiadujemy się jakie otrzymuje wynagrodzenie, ile wypija mleka, jakiej wielkości posiada mieszkanie, jak często chodzi do kina... 

Zbieraniem i opracowywaniem oraz udostępnianiem oficjalnych danych statystycznych w Polsce zajmuje się Główny Urząd Statystyczny (GUS). Jest on organem państwowym powołanym do zbierania informacji statystycznych z większości dziedzin życia publicznego i wybranych dziedzin życia prywatnego. Początki polskiej statystyki sięgają roku 1789, kiedy to Sejm zarządził pierwszy ogólnokrajowy spis ludności i dymów (domów). Natomiast 13 VII 1918 powstał Główny Urząd Statystyczny jako państwowa centralna instytucja statystyczna.

Czym między innymi zajmuje się GUS? Zbiera, analizuje, opracowuje i udostępnia setki statystyk. Przeprowadza m.in. Narodowy Spis Powszechny Ludności i Mieszkań czyli spis wszystkich ludzi oraz lokali znajdujących się w dniach przeprowadzania spisu na terenie kraju. Jest to operacja mająca na celu pozyskanie jak największej ilości wiarygodnych danych. Poza tym urząd statystyczny prowadzi między innymi Polską Klasyfikację Działalności czyli  umownie przyjęty podział zbioru rodzajów działalności społeczno - gospodarczej realizowanych przez podmioty gospodarcze. Również GUS zajmuje się ważnym dla przedsiębiorców rejestrem REGON, zbiorem informacji o firmach gospodarki narodowej.

GUS, zgodnie z ustalonym wcześniej harmonogramem, publikuje w określonych odstępach czasowych (miesięcznych, kwartalnych, rocznych) dziesiątki i setki rozmaitych danych i wskaźników. Dzięki temu znamy więc np. wartość Produktu Krajowego Brutto, wyniki finansowe firm, instytucji finansowych, wskaźniki: bezrobocia i inflacji, przeciętne miesięczne wynagrodzenie w gospodarce itd. itd. Statystyki te powalają ocenić jak rozwija się sytuacja gospodarcza kraju i jak wypadamy w porównaniu z innymi krajami świata.

źródła: opracowano na podstawie informacji Głównego Urzędu Statystycznego

Krzysztof MOTYCZYŃSKI w NBPortal.pl:

1. Metoda liczenia wskaźnika kosztów utrzymania zmiany przeciętnego poziomu płacy realnej w Polsce

( Zob. M.Nasiłowski: ”System rynkowy Podstawy mikro- i makroekonomii Key Text 2000

Badanie struktury wydatków różnych grup 1udności jest niezbędne do obliczenia:

* wskaźnika kosztów utrzymania i ustalenia wysokości i żądań wzrostu plac pieniężnych (nominalnych),

* wzrostu lub spadku plac realnych 1udności w jakimś okresie.

W tym celü Główny Urząd Statystyczny (GUS) prowadzi rokrocznie badania budżetów rodzinnych (gospodarstw domowych) równych grup ludności: pracowników w mieści rodzin chłopskich na wsi, emerytów i rencistów itp. Wybrane rodziny otrzymuj specjalnie przygotowane zeszyty, w których rejestrują swoje dochody i codzienne wydatki na zakupy różnych dóbr i usług (za te czynności otrzymują pewne wynagrodzenie). Przesłane na koniec roku materiały informacyjne do GUS są sumowane (za pomocą. komputerów) i ustalana jest na tej podstawie struktura wydatków w różnych przekrojach społecznych oraz przeciętna struktura wydatków dla całego kraju. Badaniem objęta jest stosunkowo niewielka liczba go­spodarstw domowych, które uznano za dostatecznie reprezentujące określone środowiska spoleczne³. Metoda reprezentacyjna jest powszechnie stosowana także w innych krajach i przynosi ona zupełnie dobre wyniki.

Rezultaty najnowszych badań zawierają poniższe dane dotyczące struktury wydatków konsumpcyjnych na jedną osobę w przeciętnym gospodarstwie domowym w Polsce w 1994 r.

Wydatki %

1. Żywność 39.9

2. Alkohol i wyroby tytoniowe 3,7

3. Odzież i obuwie 7,1

4. Utrzymanie i wyposażenie mieszkania 20,3

5. Transport i łączność 9,2

6. Nauka 1,8

7. Kultura i wypoczynek 5,3

8. Zdrowie i higiena osobista 6,6

9. Pozostałe wydatki 6,1

Razem 100

Źródło: Mały rocznik statystyczny 1995, GUS. Warszawa 1995. s. 118.

Do obliczenia wskaźnika kosztów utrzymania trzeba ustalić nie tylko struktur przeciętnych wydatków 1udności, ale także wskaźnik wzrostu cen w poszczególnych grupach towarowych. W tym celu GUS opracował tzw. reprezentacyjny koszyk zakupów dla wszystkich ludzi w Polsce. Obejmuje on około 1800 produktów re­prezentujących różne grupy towarowe dla mężczyzn , kobiet i dzie­ci. Następnie prowadzi się dokładną rejestracje wzrostu cen towarów reprezentantów w ciągu roku i oblicza się przeciętny wzrost cen poszczególnych grup wydatków w ciągu roku.

W celu uproszczenia obliczeń posłużmy się wskaźnikami wzro­stu cen towarów i usług konsumpcyjnych ograniczonymi do czte­rech podstawowych grup wydatków.

Grupy wydatków Wskaźnik

1. Żywność 133,0
2. Napoje alkoholowe i wyroby tytoniowe 128,9
3. Towary nieżywnościowe 131,0
4. Usługi 133,0

W Polsce w 1994 r. badaniem budżetów gospodarstw domowych objęto 32 085 gospodarstw . Ze wzglądu na to. że ogólna liczba gospodarstw domowych jest szacowna na około 10,7 ml , przeto zaledwie 0.3% objętych jest badaniami statystycznymi

Struktura wydatków w badanych gospodarstwach domowych. dostosowana do wymienionych wyżej czterech grup, kształtowała się następująco :

Grupy wydatków %

1. Żywność 39,9
2. Napoje alkoholowe i wyroby tytoniowe 3,7
3. Towary nieżywnościowe 29.0
4. Usługi 27,4
Razem 100,00

Przy obliczaniu wskaźnika przeciętnego wzrostu kosztów utrzy­mania na1eży pomnożyć poszczególne wskaźniki wzrostu cen przez udziały wydatków w następujący sposób:

133,0* 0,399 + 128,9* 0,037 + 131,0* 0,29 + 133,0* 0,274 =132,2.

Z obliczeń wynika, ze wskaźnik przeciętnych kosztów utrzyma­nia ludności w 1994 r. wynosił w Polsce 132,2, czyli koszty utrzy­mania wzrosły o 132,2-100= 32,2% w porównaniu z 1993 r.

Dlaczego wybra1iśmy takie, a nie inne, wagi? Czyżby można było ustalać je na zupełnie dowolnym poziomie? Oczywiście nie można. Wpływ wskaźników cząstkowych na wysokość szukanego wskaźnika syntetycznego powinien być proporcjonalny do udziału wydatków na dane dobro w całości wydatków konsumentów na wszystkie dobra. Innymi słowy chcemy, aby szukany wskaźnik syntetyczny dobrze informował o zmianie kosztów utrzymania zachodzącej pod wpływem ruchu cen. Skoro tak, to wagi wyznaczające silę siłę wpływu wskaźników cząstkowych na wskaźnik syntetyczny (a więc ich wartości powinny być ułamkami jedności, których wysokość dokładnie odpowiada udziałowi wydatków na dane dobro we wszystkich wydatkach konsumentów. Przecież dziesięcioprocentowy wzrost ceny dobra, na które wydatki stanowią 90% wszystkie wydatków, podnosi koszty utrzymania 9 razy więcej niż taki sam wzrost ceny dobra, którego waga w ogólnych wydatkach wynosi jedynie 10%

Podsumujmy nasze rozważania. Uzyskany dzięki odwołaniu się do zapropo­nowanej metody wskaźnik zmian( wzrostu lub spadku) cen detalicznych informuje o ruchu wszystkich cen dóbr konsumpcyjnych. Jego wysokość jednak za1eży nie tylko od tempa zmian cen poszczególnych dóbr, lecz także od struktury wydatków .Formę wskaźników, będących średnią ważoną innych wskaźników, przyjmują bardzo ważne informacje o przebiegu procesu gospodarowania. Na przykład, Główny Urząd Statystyczny oblicza w ten sposób wskaźniki zmian cen detalicz­nych dóbr konsumpcyjnych, czyli tempo inflacji w Polsce Zauważmy przy okazji, że mamy przed sobą przykład, ilustrujący ważną tezę z pierwszego wykładu. Fazę obserwacji gospodarki bardzo trudno jest oddzielić od fazy interpretowania zdobytych informacji. Jak się okazuje, stwierdzeniu, że przeciętne ceny w Polsce w sierpniu 1990 r. wzrosły o 1,8%, towarzyszą milczące założenia , które dotyczą m.in. składu koszyka dóbr-reprezentantów i wiarygodności danych uzyskanych w czasie badania budżetów gospodarstw domowych. Ktoś, kto przyjąłby inne założenia , zaobserwowałby inny poziom inflacji. W gruncie rzeczy to właśnie dlatego gospodynie domowe nie wierzą w to, co na temat inflacji pisze ,,Rzeczpospolita”.

2. Koszyk dóbr konsumenta

Dobra i usługi wchodzące w skład ,,stałego koszyka” nie u1egają w przyjętym okresie zmianie. Niemniej jednak co pewien czas — w USA co 10 lat — rząd weryfikuje ,,zawartość ” koszyka. Wybierane jest wówczas zawsze pierwszych czterysta najbardziej znaczących w wydatkach kon­sumenta pozycji. Następnie oblicza się ich udziały (wagi) w globalnej masie wydatków. Konstrukcja koszyka uwzględnia w ten sposób za­równo pozycje, jak też i ich ,,wagi”. Dany koszyk jest podstawą do ob­liczania poziomu cen dla dowolnego okresu. Najpierw ustala się dla każdej z 400 pozycji osobno relację ceny bieżącej do ceny tej samej pozycji z roku bazowego, a następnie tak uzyskaną. relację przemnaża się przez stosowną ,,wagę”. Następny etap to sumowanie wszystkich uzyskanych iloczynów. Łączną sumç przemnaża się przez sto i uzyskuje poziom cen dla badanego okresu, bądź też co jest tylko kwestią interpretacji, wskaźnik inflacji. Poziom cen obliczany jest dla okresów rocznych, kwartalnych i miesięcznych. Innymi słowy, informacje dostępne dla społeczeństwa dotyczą okresów miesięcznych i dłuższych .

3. Główny Urząd Statystyczny i wskaźniki cen

( Zob : B.Czarny i inni „Podstawy ekonomii ”)

W formie wskaźników będących średnią ważoną innych wskaźników GUS podaje informację o zmianie poziomu cen dóbr konsumpcyjnych w Polsce. Ustala on najpierw koszyk tzw. dóbr-reprezentantów. Około 1990 r. w Polsce w jego skład wchodziło od 1500 do 1800 typowych towarów konsump­cyjnych (m.in.: mintaj wędzony, odgłowiony, 1 kg; przełącznik klawiszowy, podtynkowy; papierosy ,,Ekstra Mocne”; strzyżenie zwykle w zakładzie usługowym męskim kat. 3). Skład tego koszyka aktualizowano, w wyniku czego co roku wymianie podlegało 10% dóbr. Ich ceny były następnie obserwowane przez 400 ankieterów w 307 rejonach statystycznych w całym kraju. Na przykład, notowania cen żywności, alkoholu i papierosów odbywały się 3 razy w miesiącu w sklepach, na targowiskach, w stołówkach i restauracjach. Dane te pozwalały ustalié cząstkowe wskaźniki zmian cen poszczególnych dóbr z dekady na dekadç konkretnego miesiąca.

Rolę wag przy obliczaniu poziomu syntetycznego wskaźnika inflacji odgrywały, oczywiście, udziały wydatków na poszczególne dobra w całości wydatków przeciętnej polskiej rodziny. Ich wysokość ustalano na podstawie notatek prowadzonych regularnie na zlecenie GUS przez 10 tysięcy wy­branych rodzin, które rejestrowały swoje wydatki i dochody (s4 to tzw. badania budżetów gospodarstw domowych). Ponieważ ankietowani zwykle zaniżają dane o swoich wydatkach na alkohol, papierosy i usługi gastro­nomiczne, potrzebna była korekta, której dokonywano na podstawie infor­macji o sprzedaży detalicznej tych dóbr. (Wydatki na tomiki poezji nie były korygowane). Publikowane przez GUS i prasç co miesiąc wskaźniki zmiany cen powstają na podstawie wag obliczonych w taki sposób dla roku poprzedniego. To właśnie nie one są podane w tablicy

4. Z. Matkowski: „Podstawy ekonomii .Mikroekonomia „ Wyższa Szkoła zarządzania i przedsiębiorczości im. Bogdana Jańskiego 1999 ss. 23-24

W rzeczywistości przy wyznaczaniu ogólnego wskaźnika cen towarów i usług konsumpcyjnych, który jest przybliżoną miarą inflacji, Główny Urząd Statystyczny (GUS) bierze pod uwagę średnie notowania na terenie całego kraju (w danym miesiącu lub roku) cen konkretnych towarów i usług uznanych za najważniejsze i najbardziej charakterystyczne w strukturze wydatków przeciętnej rodziny polskiej. Lista takich towarów i usług jest co pewien czas aktualizowana i obejmuje od 1000 do 2000 pozycji. Oto niektóre z nich:

a) żywność chleb mieszany zwykły, makaron jajeczny, ziemniaki, cebula , mięso wieprzowe z kością kiełbasa ,,Toruńska”, karp świeży , śledź solony odgłowiony, smalec, margaryna deserowa ,,Palma”, mleko krowie spożywcze, jaja kurze świeże, cukier biały kryształ, herbata ,,Madras”, kawa naturalna mielona ,,Tchibo Familly” (do 1995 r. — ,,Ekstra Selekt”), dżem truskawkowy, galaretka o smaku różnym, pieprz naturalny;

b) używki: wódka ,,Stołowa Wódka Czysta”, wino gronowe białe wytrawne, piwo jasne pełne, papierosy ,,Caro”;

c) odzież obuwie: ubranie męskie dwuczęściowe z elanobawełny czesan­kowej, koszulka gimnastyczna na 6—11 lat, rajstopy damskie elastyczne, kozaki skórzane na podeszwie nieskórzanej;

d) sprzęt gospodarstwa domowego: kanapa dwuosobowa rozkładana, dy­wan strzyżony żakardowy, ręcznik 50 x 100 cm frotte, pralka elektrycz­na ,,Gracja” , zamrażarka domowa 100 l, wanna kąpielowa emaliowana, żelazko bez nawilżacza, garnek emaliowany bez pokrywy, szklanka gładka bezbarwna, żarówka zwykła 60 W, pasta do obuwia;

e) środki ochrony zdrowia: spirytus salicylowy, koszyczek rumianku pospolitego, raphacholin w drażetkach, termometr lekarski z futerałem;

f kosmetyki wyroby toaletowe: mydło toaletowe ,,Fa”, pasta do zębów ,,Pollena”, krem do golenia ,,Pollena”, proszek do prania ,,Pollena”, ostrze ,,Polsilver”, papier toaletowy;

g) książki, gazety i art. piśmienne : brulion 96-kartkowy, długopis ,,Zenith”, dziennik ,,Życie Warszawy”, tygodnik ,,Przyjaciółka”;

hi) inne wyroby przemysłowe: zegarek męski elektroniczny na rękę błona fotograficzna ,,Kodak”, butla turystyczna na gaz, rower turystyczny, samochód osobowy ,,Fiat CinqueCento”, obrączka złota próby 0,583;

I) usługi: podzelowanie klejonego obuwia męskiego, ondulacja trwała na zimno, upranie z wykończeniem bielizny pościelowej, bilet normalny na przejazd pościgiem osobowym na odległość 91—100 kin, list zwykły zamiejscowy , centralne ogrzewanie za 1 m², gaz z sieci za 1 m³, bilet normalny do Teatru Polskiego w Warszawie — rząd XVI, miejscowa rozmowa telefoniczna — za jednostkę licznikową

Podawane do wiadomości publicznej wskaźniki inflacji wyrażają jedynie uśredniony wzrost cen towarów i usług uwzględnianych w statystycznym koszyku konsumenta. jeżeli struktura naszych wydatków różni się od tego wzorca (tzn. jeśli zamiast pasty do zębów ,,Pollena” używamy pasty ,,Col­gate”, unikamy tłuszczów zwierzęcych i alkoholu lub jeździmy innym samochodem niż ,,Fiat Cinquecento”), to nasze odczucia co do wzrostu kosztów utrzymania będą odbiegać od mierzonego statystycznie tempa inflacji.

Samochody realnie cenione

W 1994 roku maluch kosztował tyle ile 1035 butelek wódki, a w 1998 tyle, ile 621 flaszek

Tanieją auta! Widać to, gdy porównamy ich cen z naszymi zarobkami lub cenami innych towarów. W 1994 roku na opla as trę trzeba było wy­dać aż 50 przeciętnych pensji. W ze­szłym roku już tylko 28, czyli tylko, ile na poloneza cztery lata temu - wyni­ka z raportu firmy Boss.

Do 1994 roku inflacja i ceny samo­chodów szły w górę niemal łeb w łeb. Jednak pięć lat temu ich ścieżki roze­szły się. Samochody drożeją wolniej niż inne towary. Dlaczego?

Celne powody

Powodów jest kilka. Najważniejszy to malejące co roku o 5 punktów procentowych cło. W 1994 roku za auta zagraniczne produkowane w Unii Europej­skiej trzeba było płacić cło stanowiące 35 proc. ich wartości, a za samochody z krajów byłego bloku socjalistycznego aż 70 proc. W tej chwili cło na samo. chody z UE wynosi 15 proc., a na auta z krajów dawniej socjalistycznych 20 proc.

Polacy kupują też coraz więcej sa­mochodów W ubiegłym roku na na­sze drogi wyjechało ponad pół, milio­na nowiutkich aut. Dla producentów chłonny rynek to nie lada gratka, ale konkurencja wymusza na nich obniża­nie cen. Firmy sprzedają niektóre mo­dele poniżej kosztów, aby utrzymać się na naszym bardzo atrakcyjnym rynku. Najbardziej korzystają na tym ci, którzy zdecydowali się kupić auta trochę lepsze niż średnie z tzw. seg­mentu C (np.. toyota corolla, opel astra): Nieco mniej staniały auta klasy B i A; czyli te najmniejsze, a więc naj­częściej kupowane (np.. maluch, tico, peugeot 106).

Ile realnie warte były samochody w roku 1994 ,a ile w roku 1998
	Półlitrówek wódki		Litrów etyliny 94		przeciętnych wynagrodzeń
Rodzaj samochodu	1994	1998	1994	1998	1994	1998
Fiat 126	1035	621	6807	6114	14,34	9,13
Fiat CC Young	1589	1039	10600	16333	22	15,26
Tico	1859	1238	12399	12185	25,74	18,20
Polonez	1900	1283	12678	12623	26,32	18,85
Opel Astra	3577	1916	23860	18852	49,53	28,16

Ucieczka od inflacji

Jeśli ceny samochodów z roku 1994 wzrastałyby w takim samym tempie jak inflacja, okazałoby 'się, że ford escort 1,3 kosztowałby dzisiaj 51 tysię­cy zł. Byłby zatem o 60 proc. droższy niż modele oferowane w salonach, gdzie żądają ok. 32 tys.. zł. Tak samo potraktowana cena toyoty corolli wy­nosiłaby 72 tys.. zł, czyli byłaby wyższa od obecnej aż o 89 proc. (38 tys., zł). Za poloneza caro musielibyśmy zapła­cić 26 600 zł a nie 20,1 tys..

Najpopularniejszy na naszych dro­gach fiat 126 w 1994 roku kosztował 7 500 zł. Dzisiaj trzeba za niego zapła­cić 11 190 zł: To oczywiście więcej ale gdyby cena malucha rosła tak jak infla­cja, wynosiłaby 14 515 zł.

Samochody tak naprawdę są jesz­cze tańsze, niż wynikałoby z przedsta­wionych wyliczeń. Ważne jest bowiem nie tylko ile, ale i za co płacimy. A przecież podstawowe wersje aut w 1994 roku były dużo skromniej wy­posażane niż obecnie. Dla przykładu tegoroczna standardowa astra ma dwie poduszki powietrzne i system ABS. W 1994 za te dodatki trzeba by­ło dopłacać, i to kilkanaście tysięcy. Ponadto dzisiaj produkowane auta są zmodernizowane, a więc teoretycznie powinny być lepsze od swoich po­przedników.

Rdzewiejące ceny

Realnie coraz tańsze są też samochody używane. Rocznie ich nominalna cena wzrasta najwyżej o 5 proc., choć są też modele, które ostatnio tylko tanieją. Na spadek cen samochodów używa­nych duży wpływ miały promocje na auta nowe oraz dostępność do kredy­tów na kupno samochodu. Coraz wię­cej osób dylemat, czy kupić używam a tańszy, czy nowy a droższy, rozstrzyga na korzyść drugiego rozwiązania.

W 1995 roku ceny samochodów używanych były o 25 proc. wyższe niż w 1994 roku. Odpowiada to inflacji za 1994 rok. W 1996 ceny aut wzrosły o 7 do 10 proc. Natomiast rok temu niektóre ceny były niższe niż w 1997 roku. Dotyczy to np.. rocznego tico, którego cena spadła z 19 tys.. na 18 800 czy rocznego fiata 126, który w 1997 roku kosztował 10 800 zł, w ze­szłym roku 10 tys. zł. Zatem spadały nie tylko ceny realne, ale mimo inflacji również ceny nominalne.

Jak długo utrzyma się taka tenden­cja, trudno dziś wyrokować. Jednak co roku specjaliści wypowiadają się, że taniej aut sprzedawać już nie można, a po kilku miesiącach okazuje się że jednak można.

W matematyce po raz pierwszy terminu funkcja użył w roku 1692 G.W. Leibniz* (1646-1716)

Prawo głosi , że jeśli będziemy powiększali ilości czynnika zmiennego np. pracy kolejno o takie same jednostki (w naszym przykładzie o ΔLx=1) i dodawali ją do stałych ilości pozostałych czynników wytwórczych (kapitału i ziemi), to uzyskiwane z dodatkowej jednostki pracy przyrosty produkcji ΔX/ΔLx, zwane produktem krańcowym lub marginalnym będą najpierw coraz większe, po przekroczeniu pewnego krytycznego poziomu) punkt przegięcia funkcji) stają się coraz mniejsze, wreszcie od pewnego poziomu zatrudnienia produkt krańcowy pracy ludzkiej z dodatniego zmienia się na ujemny

W tej sytuacji, o czym będziemy pisać dalej, zmienił się stosunek ceny zeszytu do ceny segregatora i na odwrót, czyli tzw ceny względne. Zmiany tego typu są rzadko spotykane w krótkim okresie, gdzie wszystkie ceny rosną w podobnym tempie. Jednakże, gdy analizujemy szeregi czasowe w dłuższym okresie, to z takimi zmianami spotykamy się bardzo często.

X	ΔX	Y	ΔY	tg  YX	tg  Y/X
0		0
10	10	10	10	10/10 = 1	10/10 = 1
20	10	20	10	10/10 = 1	20/20 = 1
30	10	30	10	10/10 = 1	30/30 = 1
40	10	40	10	10/10 = 1	40/40 = 1

X	X	Y	Y	tg  YX
0	0	0	0
1	1	5	5	5
2	1	9	4	4
3	1	12	3	3
4	1	14	2	2

Kombinacje	C	Q0	Q1	Q =Q0-Q1
a	11	0	2	2-0 = 2
b	10	1	3	3-1 = 2
c	9	2	4	4-2 = 2
d	8	3	5	5-3 = 2
e	7	4	6	6-4 = 2

Indeks łańcuchowy z badanego roku _* indeks

o stałej podstawie za rok poprzedni

-----------------------------------------

100

Wskaźnik o stałej podstawie

dla roku t = 100

=

---