004 (18)

A. Egzamin poprawkowy z matematyki dla studentów I Energetyki w sem. II. Pytania z teorii. Pytania 1-5 po 3pt. Pytania 6-8 po opt. 15.09.2009

Uwaga! Obowiązuje kolejność odpowiedzi na pytania.

1.    Definicja całki niewłaściwej funkcji f(x) określonej na przedziale < a, b) imeogramczont^

2.    Ekstrema funkcji uwikłanej. Warunek konieczny i dostateczny.

Twierdzenie o zamianie całki krzywoliniowej skierowanej na całkę oznaczoną.

4. Warunki Cauchy’ego-Riemanna holomorficzności funkcji zespolonej, o 5. Odwzorowanie konforemne. Definicja i przykłady.

^J 6. Definicja całki oznaczonej funkcji f{x) na przedziale < a,b >.

7.    Czynnik całkujący i algorytm znajdowania czynnika całkującego równania różniczkowego P(x,y)dx + Q(x.y)dy = 0, gdy czynnik całkujący zależy tylko od x.

8.    Twierdzenie o rozwijaniu funkcji zespolonej f(z) w szereg Taylora.

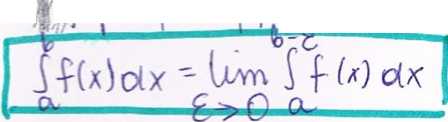
■    )r& &

\SpgXh. COlWtaAo

Mi

(jjptoa. toctfrafe, CouLctc

‘ ^r dK/reiUmą ¹

XaA. £

Cooku 0k.nac3cv\a

-roxd^jetamu pu&dtial - Suma, caflobwfc Sn*« -i&żSJU itinC&z UrnS.^

Ctaou <pcdxM6u/’T od uxii^ bimxWr^

S    ii

: *]j4ⁿi¹ n<b<-^|-'C0 U

|7^wd>JfeŁffW<fa

i-4