050 051

50 *

o

1	I	1 1	1	1	1	1 V	•	1	•	-
1	1	• 1	1	1	1	1 V	I	-	1	1
1	1	1 1	1	1	1	1 V	1	t	-	1	✓
ł	1	1 1	1	1	1	i V	-	1	1	1	/
1	1	1 1	1	1	1	i y	1	—	1	1
1	1	1 t	i	1	I	1 V	—	1	1	1	V
i	ł	1 1	1	t	1	%v	1	i	-	1	/
1	1	1 1	1	1	1	1 V	!	1	1	-

	1 1 t 1	1 1 I 1	• lit	1 1 1 t	1 1 1 1	t 1 » 1	11 1 1	1 1 1 1
III-		*	X
1 - ) 1	X			X
1 -1 t					X	X
tli-							X	X
- 1 - 1			X	X		X		X

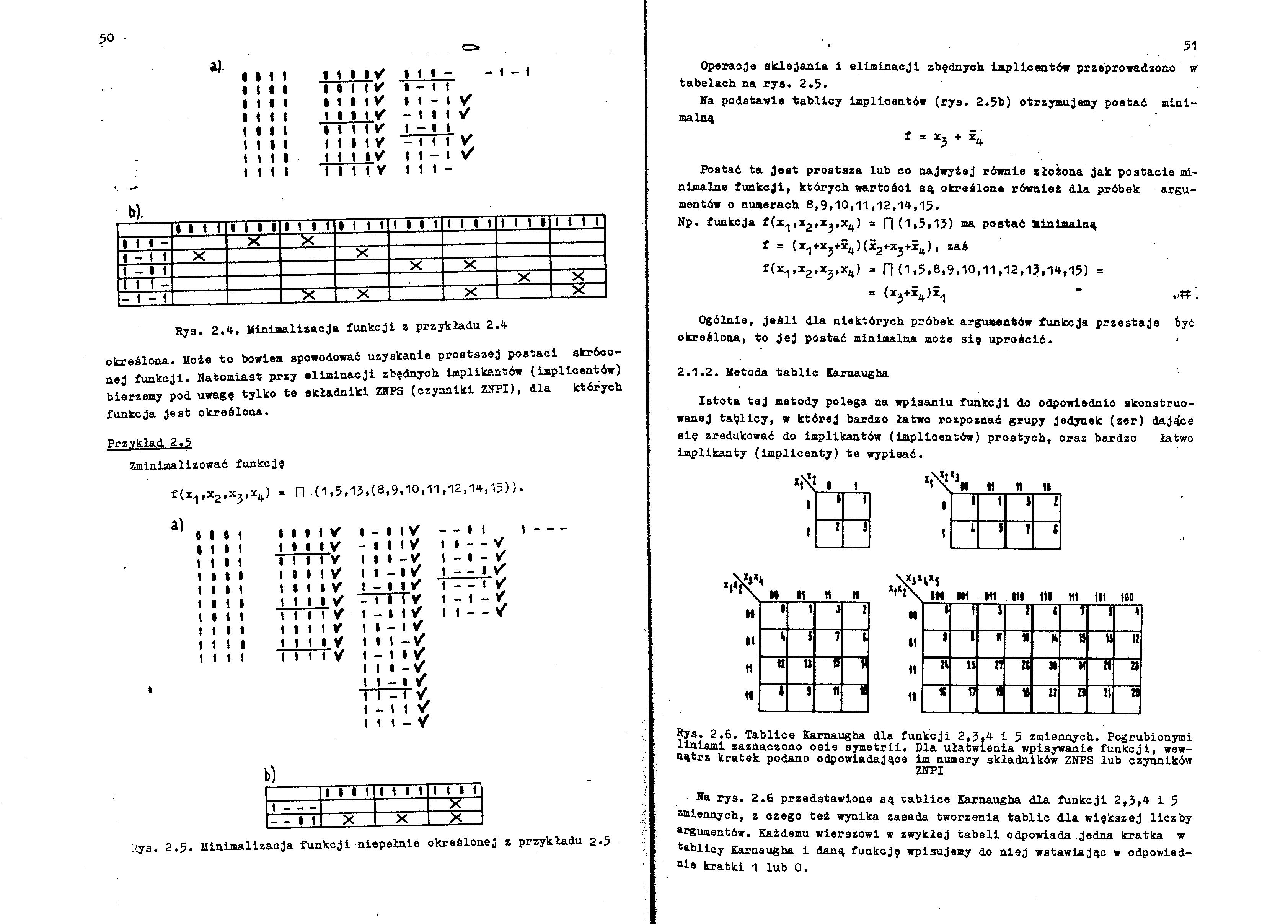
Rys. 2.4. Minimalizacja funkcji z przykładu 2.4

określona. Może to bowiem spowodować uzyskanie prostszej postaci skróconej funkcji. Natomiast przy eliminacji zbędnych implikantów (implicentów) bierzemy pod uwagę tylko te składniki ZNPS (czynniki ZNPI), dla których funkcja jest określona.

Przykład 2.5

Zminimalizować funkcję

f i )	=	n		(1,5,	15,(8,9,10,	11,12,14,15))
a) 116 1	•	•	i	i y	l - i l V	- - I I
1 t 1 1	1	i	i	» V	-11 i y	i l - - V
1111	1	i	i	1 V	i • • -y	1 - 1 - /
116 6	1	i	i	1 y	ll-l/	i -- a y
1111	1	i	i	• V	i - i i ✓	i - - i y
tlił	1	i	i	6 ✓	- i i i y	i - i - /
16 11	1	i	i	l V	i - i t ✓	ii--/
1111	1	i	i	i y	i i - i y
1116	1	i	i	i y	1 1 1 -✓
1111	1	i	i	\ y	1-11/
					III -V
					i i - i /
					rr iry
					i - i i /
					i i i - y

b)

	liii	liii	1 t 1 1
1---			X
- - i i	X	X	X

liys. 2.5. Minimalizacja funkcji niepełnie określonej z przykładu 2.5

Operacje sklejania 1 eliminacj1 zbędnych impllcentów przeprowadzono w tabelach na rys. 2.5.

Na podstawie tablloy impllcentów (rys. 2.5b) otrzymujemy postać minimalną

^f = *3 ^{+ 5}4

Postać ta Jest prostsza lub co najwyżej równie złożona jak: postacie minimalne funkcji, których wartości są określone również dla próbek argumentów o numerach 8,9,10,11,12,14,15.

Np. funkcja    Xj»x₄) = li (1,5,13) ma postać minimalną

f = (x₁+x_J+x₄)(x₂+x₅+x₄), zaś £i^2**3»*ą) ³ n (1,5,8,9,10,11,12,13,14,15) =

=

Ogólnie, jeśli dla niektórych próbek argumentów funkcja przestaje być określona, to jej postać minimalna mole się uprościć.    • 2.1.2. Metoda tablic Karaaugha

Istota tej metody polega na wpisaniu funkcji do odpowiednio skonstruowanej tablicy, w której bardzo łatwo rozpoznać grupy jedynek (zer) dające się zredukować do implikantów (impllcentów) prostych, oraz bardzo łatwo implikanty (impllcenty) te wypisać.

*1^ •

1

■Nft,

1)

n

u

i

1

1

•

i

1

i

i

i

i

i

1

i

i

7

t

AS \ *»

u

n

N

W *i*K

IM

Ni

m

III

ni

W

m

im

ll

1

i

s

I

N

i

1

i

i

i

T

"Hf

9

li

s

7

t

11

i

1

ti

U

H

a

19

17

«

tl

u

B

«

<1

»

li

n

n

91

91

H

»

W

*

1

11

i

11

«

17

ń

«

U

a

ti

a

Rys. 2.6. Tablice Karaaugha dla funkcji 2,3,4 1 5 zmiennych. Pogrubionymi liniami zaznaczono osie symetrii. Dla ułatwienia wpisywanie funkcji, wewnątrz kratek podano odpowiadające im numery składników ZNPS lub czynników

ZNPI

Ra rys. 2.6 przedstawione są tablice Karaaugha dla funkcji 2,3,4 i 5 zmiennych, z czego też wynika zasada tworzenia tablic dla większej liczby argumentów. Każdemu wierszowi w zwykłej tabeli odpowiada Jedna kratka w tablicy Karaaugha i daną funkcję wpisujemy do niej wstawiając w odpowiednie kratki 1 lub 0.