076 077

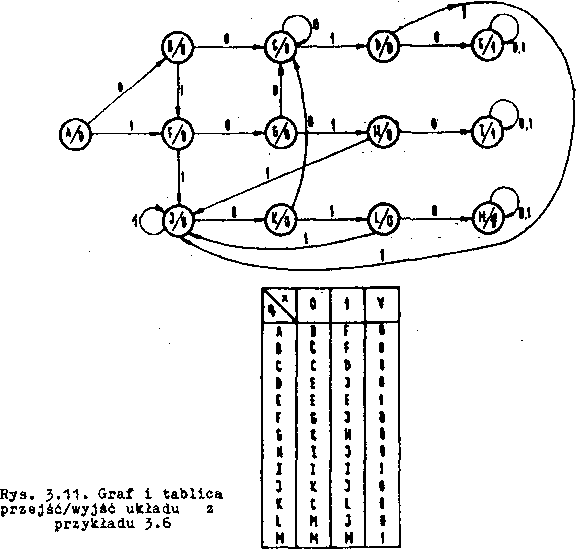
76

X X	X
x	X	X
X	X	X	X
X	CS FI	X	X	X
X	X	OH	X	X	X
X	X	X	u	X	X	X
X	X	X	X	V	X	X	X
X	CK U	sy	X	X	H	X	X	X
X	X	Dl	X	X	X	HI	X	X	X
X	X	-łk	EH	X	X		IM	X	X	X
X	X	X	X	V	X	X	X	V	X	X	X

ADCDEFSHIJKl

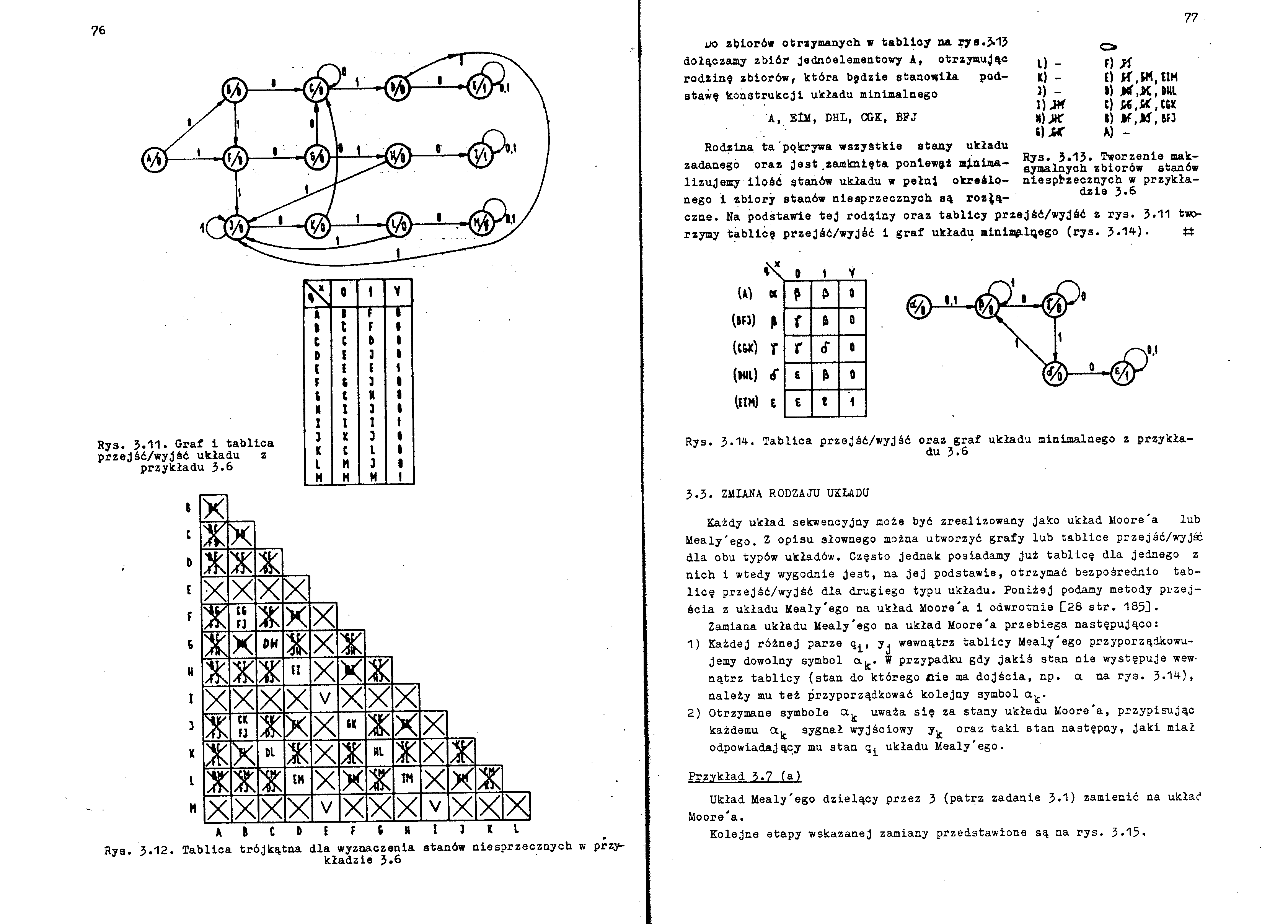
Rys. 3.12. Tablica trójkątna dla wyznaczania stanów niesprzacznych w przykładzie 3*6

do zbiorów otrzymanych w tablicy na rys.3.13 dołączamy zbiór Jednóelementowy A, otrzymując rodzin? zbiorów, która będzie stanowiła podstaw? konstrukcji układu minimalnego

O

U -    f)    fi

K) -    i)    ft ,{M, tIM

3) - ł)#r,K,Mll IUK    t)    P€,«f,C6K

H)JHT    »)    JK.Jtf.W3

t) JUT    A)    -

Rys. 3.13* Tworzenie maksymalnych zbiorów stanów niespbzecznych w przykładzie 3-6

A, ElM, DHL, CGK, BFJ

Rodzina ta pokrywa wszystkie stany układu zadanego oraz jest .zamknięta ponieważ minimalizujemy ilość stanów układu w pełni określonego i zbiory stanów niesprzecznych są rozją-czne. Na podstawie tej rodziny oraz tablicy przejść/wyjść z rys. 3-11 tworzymy tablic? przejść/wyjść i graf układu minimalnego (rys. 3.14). tt

	0	i	*
M *	P	(i	0
(5F3) p	f	6	0
M T	r	<r	t
(Wl) <f	t	p	0
lnu) 1	i	t	i

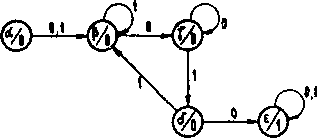
Rys. 3.14. Tablica przejść/wyjść oraz graf układu minimalnego z przykładu 3.6

3.3. ZMIANA RODZAJU UKŁADU

Każdy układ sekwencyjny może być zrealizowany Jako układ Moore'a lub Mealy'ego. Z opisu słownego można utworzyć grafy lub tablice przejść/wyja: dla obu typów układów. Często Jednak posiadamy już tablic? dla jednego z nich i wtedy wygodnie jest, na jej podstawie, otrzymać bezpośrednio tablicę przejść/wyjść dla drugiego typu układu. Poniżej podamy metody przejścia z układu Mealy'ego na układ Moore'a i odwrotnie C28 str. 1853. Zamiana układu Mealy'ego na układ Moore'a przebiega następująco:

1)    Każdej różnej parze yj wewnątrz tablicy Mealy'ego przyporządkowujemy dowolny symbol a.^. W przypadku gdy jakiś stan nie występuje wewnątrz tablicy (stan do którego Ole ma dojścia, np. a na rys. 3-14), należy mu też przyporządkować kolejny symbol a^.

2)    Otrzymane symbole    uważa się za stany układu Moore'a, przypisując

każdemu    sygnał wyjściowy y_t oraz taki stan następny, jaki miał

odpowiadający mu stan układu Mealy'ego.

Przykład 3.7 (a)

Układ Mealy'ego dzielący przez 3 (patrz zadanie 3.1) zamienić na układ Moore'a.

Kolejne etapy wskazanej zamiany przedstawione są na rys. 3-15.