img102

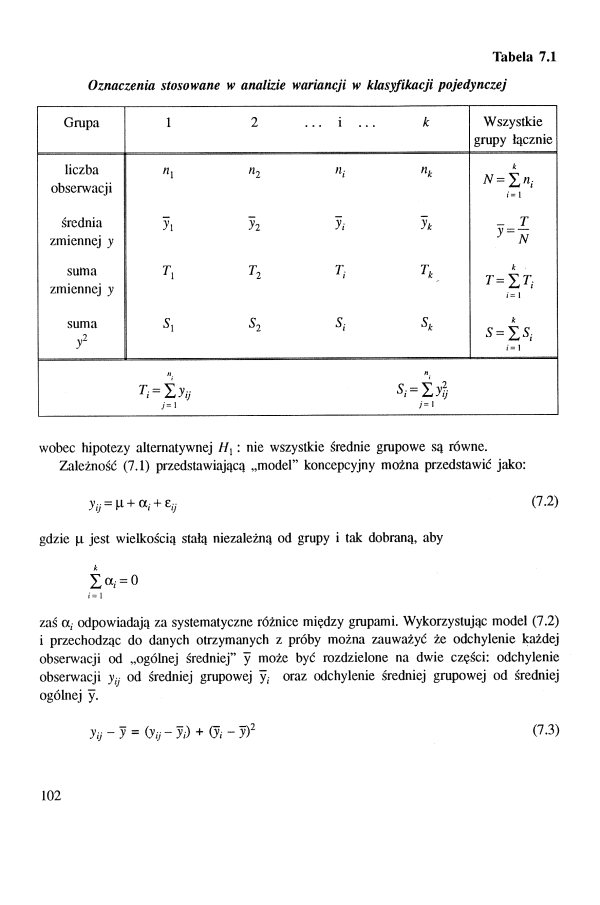
Tabela 7.1

Oznaczenia stosowane w analizie wariancji w klasyfikacji pojedynczej

Grupa	i	2	... ; ..	k	Wszystkie grupy łącznie
liczba obserwacji	”i	n2	”,		N = £ ”, i-i
średnia	h	%	y	>'k	_ T
zmiennej y					^J N
suma zmiennej y		T2	Tt	Tk
suma 2 y		Si	Si	sk	s=is, /-1
				,
	n			s,-±Ą
	;= i			>» i

wobec hipotezy alternatywnej //,: nie wszystkie średnie grupowe sa równe.

Zależność (7.1) przedstawiająca „model” koncepcyjny można przedstawić jako:

y_(> = p + «, + e_jy    (7.2)

gdzie (i jest wielkością stała niezależna od grupy i tak dobrana, aby

Z«, = 0

i»l

zaś a, odpowiadają za systematyczne różnice między grupami. Wykorzystując model (7.2) i przechodząc do danych otrzymanych z próby można zauważyć że odchylenie każdej obserwacji od „ogólnej średniej” y może być rozdzielone na dwie części: odchylenie obserwacji y_i} od średniej grupowej y, oraz odchylenie średniej grupowej od średniej ogólnej y.

y\j -y = (y,>- - y.) + <yi-y)²    (⁷-3)

102