img049

106 II. Parametryczne testy istotDości

§ 2.9. TEST ANALIZY WARIANCJI (KLASYFIKACJA

PODWÓJNA)

Podstawowe wyjaśnienia

Podany w poprzednim paragrafie 2.$. model analizy wariancji dotyczył klasyfikacji pojedynczej, tzo. wyniki obserwacji badanej cechy klasyfikowano na k grup według jednego kryterium (czynnika).

W zastosowaniach zachodzi nieraz potrzeba klasyfikacji wyników obserwacji według widu naraz kryteriów. Przy dwóch kryteriach mówimy o tzw. klasyfikacji podwójnej. Z klasyfikacją podwójną mamy do czynienia w takich eksperymentach statystycznych, w których na realizację badanej zmiennej losowej mogą wpływać dwa niezależne czynniki dające addytywne (sumujące się) efekty. Wykrycie istotnego wpływu każdego z tych dwu czynników na realizację badanej w doświadczeniu zmiennej losowej jest możliwe dzięki zastosowaniu odpowiedniego testu statystycznego dla wielu średnich- Omawiany tu test stosuje się na przykład w często używanym typie eksperymentu statystycznego jakim jest doświadczenie metodą bloków losowych.

Podstawą testu analizy wariancji według klasyfikacji podwójnej jest rozbicie sumy kwadratów wariancji wyników próby na trzy składniki odpowiadające zmienności wywołanej pierwszym czynnikiem, drugim czynnikiem oraz zmienności reszt owej. Obliczenia prowadzi się w specjalnej tablicy analizy wariancji w celu uzyskania wartości statystyki F dla dwu testów odpowiadających badaniu istotności wpływu obu czynników'.

Klasyfikację n obserwacji zmiennej losowej J na r grup według przyjętego pierwszego kryterium (czynnik A) i na k grup według drugiego kryterium (czynnika B) możemy zapisać jako tablicę:

!>-	B	1	2	...	k
i		*n	*ii	...	x,t
2				...	-tu
r			Xrl	...	*r*

§ 2,9, Test analizy wariancji (klasyfikacja podwójna)

107

Występujące w tej tablicy liczby x_tj (i= 1,2,,.., r; j= 1,2, fc) oznaczają zaobserwowane w doświadczeniu w grupie (zer względu na czynnik A) oraz jednocześnie w grupie j (2c względu na czynnik B')> wartości badanej cechy X, Należy zwrócić uwagę, że podobnej tablicy (tablica niezależności ) używa się w teście niezależności podanym w § 3.3, jednakże we wnętrzu tamtej tablicy wpisuje się liczebności, a nic wartości mierzalnej cechy X\ jak to ma miejsce tutaj.

W każdej klasyfikacyjnej podgrupie tj. w kratce (i,/) występuje tylko jedna obserwacja (np. ze względu na wysokie koszty eksperymentu). Poszczególne grupy w podziale według przyjętych dwóch kryteriów mogą oznaczać np. różne poziomy natężenia czynników mających oddziaływać na wartości badanej cechy X.

Model. Danych jest r¹k populacji o rozkładzie normalnym    x),

gdzie i= 1,2.....r; /= 1,2, ..._t k, a (t jest nieznane, Z każdej z tych po

pulacji wylosowano niezależnie po jednej obserwacji x_iJy otrzymując rk obserwacji zestawionych w tablicy o r wierszach i k kolumnach¹ Na podstawie tych obserwacji należy- zweryfikować hipotezę o ich jednorodności, tj. hipotezę /7₀: m_u = m₁₂^...=»i_rłt źe wszystkie wartości średnie tn_ti są równe, wobec alternatywnej hipotezy H_ly ie nie wszystkie średnic m_ŁJ są sobie równe. Hipotezę H₀ na gruncie eksperymentu statystycznego z podwójną klasyfikacją można interpretować jako brak istotnego wpływu klasyfikacyjnych czynników na wartości obserwowanej cechy X,

Test istotności dla hipotezy H_Q jest następujący:

Z wyników obserwacji x,_i obliczamy: średnie arytmetyczne w wierszach

(2.17)

średnie arytmetyczne w kolumnach

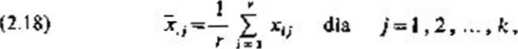
średnią arytmetyczną ogólną

(2.19)

1

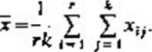
r.=T I dla    i = l, 2,... ,r,

K j=t