29 (480)

76 II. Parametryczne testy istotności

§ 2.3. TEST DLA WSKAŹNIKA STRUKTURY (PROCENTU)

Podstawowe wyjaśnienia

W badaniu statystycznym prowadzonym ze względu na cechę niemie® rzalną (jakościową) zachodzi czasem konieczność sprawdzenia hipotezy o wartości wskaźnika struktury populacji, tj. frakcji elementów wyróżnigW nych w populacji (lub po przemnożeniu przez 100 — procentu). Wskaźnik™! struktury p populacji generalnej może przyjąć wartość z przedziału (0,1).,. Hipotezę dotyczącą wartości wskaźnika struktury p można sprawdza® wieloma metodami (między innymi za pomocą analizy sekwencyjnej® W niniejszej książce omówiony będzie test dla wskaźnika struktury p dla przypadku dużej próby. Korzysta się bowiem wtedy z założenia, że wskaźM nik struktury z próby m/wma rozkłąd asymptotycznie normalny. Pozwalaj to na zbudowanie obszaru krytycznego w oparciu o rozkład normaln^H

Model. Populacja generalna ma rozkład dwupunktowy z parametrem p_t tzn. frakcja elementów wyróżnionych w populacji jest p. Z populacji tej wylosowano niezależnie do próby dużą liczbę n elementów populacja (n>100). W oparciu o wyniki tej próby, należy zweryfikować hipotez® H₀ : p— po wobec hipotezy alternatywnej H_x: p^Po, gdzie p₀jest hipotety® czną wartością parametru p.

Test istotności dla tej hipotezy jest następujący. Obliczamy wskaźnik struktury z próby m/n, gdzie m jest liczbą elementów wyróżnionych znal^H zioną w próbie. Następnie obliczamy wartość statystyki

m

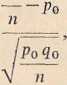
gdzie 5o = l-Po*

(2.6)

Statystyka ta ma przy założeniu prawdziwości hipotezy H₀ rozkład asymptc* tycznie normalny N(0,1). Z tablicy rozkładu normalnego N(0,1) zna* dujemy następnie taką krytyczną wartość u_a> by spełniona była równoM P{|U|>«₍₄}=a (por. rys. 4, str. 57). Zbiór określony nierównością w na*j wiasie jest dwustronnym obszarem krytycznym testu, tzn. gdy z porówna®

obliczonej wartości u z wartością krytyczną u_a wyniknie, że |w| ^ u_a, wówczas hipotezę H₀ odrzucamy na korzyść alternatywy H_x. Natomiast gdy zajdzie nierówność \u\<u_ai nie ma podstaw do odrzucenia hipotezy H₀.

Uwaga. Podobnie jak w innych testach, dwustronnego obszaru krytycznego określonego nierównością \u\^u_a używamy tylko wtedy, gdy hipoteza alternatywna jest postaci H_x:    Dla hipotezy alternatywnej

postaci H_x: p<p₀ obszar krytyczny w omawianym teście istotności buduje się lewostronnie, tzn. taka wartośću_ajest wartością krytyczną¹, że P{U^u_a}= =a. Obszar krytyczny jest wtedy określony przez nierówność t/<w_a. Wartość w_a jest wtedy oczywiście ujemna. Natomiast dla hipotezy alternatywnej postaci H_y\ p>Po obszar krytyczny w tym teście buduje się prawo-stronnie, tzn. jest on określony nierównością U^u_a. Wartość krytyczną u_x odczytuje się wtedy z tablicy rozkładu N(0, 1) w taki sposób, by spełniona była równość P{U^u_k}=cł (por. rys. 6, str. 58).

Przykład. Wysunięto hipotezę, że wadliwość produkcji pewnego podzespołu w aparatach radiowych wynosi 10%. W celu sprawdzenia tej hipotezy wylosowano niezależnie próbę 100 podzespołów i otrzymano w niej 15 podzespołów wadliwych. Na poziomie istotności a=0,05 zweryfikować tę hipotezę.

Rozwiązanie. Z treści zadania wynika, że w próbie otrzymano

m

n

15

TÓO

=0,15 = 15%

wadliwych podzespołów. Obszar krytyczny testu można zbudować tu dwustronnie.

Formalnie pisząc, stawiamy hipotezę H₀ : y; = 0,l wobec hipotezy alternatywnej H_x : p #0,1. Z tablicy rozkładu normalnego N(0,1) odczytujemy taką wartość w_a, by P(|E/j>««}== 0,05. Jest to wartość u_a= 1,96. Na podstawie wzoru (2.6) obliczamy następnie wartość

0,15-0,10 0,05-10

/0,1 • 0,9	0,3
V ioo

Porównując wartość u z wartością krytyczną u_a, mamy |u| = 1,67 < 1,96 = w_a, co oznacza, że nie znaleźliśmy się w obszarze krytycznym. Nie ma zatem (podstaw do odrzucenia hipotezy H₀, że wadliwość wynosi 10%. Różnica p %, otrzymana w próbie, okazała się nieistotna.