skanuj0009

6o    II. Parametryczne testy istotności

Test istotności dla tej hipotezy jest następujący.' Z'wyników obli prób obliczamy wartości średnie x_x i x₂ oraz wariancje i sj, a następnie wartość statystyki t według wzoru

*1~*2

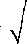
nis\ + n₂s\ ( 1 n_t + n₂ — 2 \«!

Statystyka ta ma przy założeniu prawdziwości hipotezy H_Q rozkład t Studenta o «_t+«2—2 stopniach swobody. Z tablicy rozkładu t Studenta należy odczytać dla n_l+n₂ — 2 stopni swobody oraz dla założonego z góry poziomu istotności a taką wartość krytyczną t_a, by spełniona była równość jP{|t|    Nierówność |f|określa dwustronny obszar krytyczny

testu, tzn. gdy porównując obliczoną wartość / z wartością krytyczną otrzymamy nierówność |/| to hipotezę sprawdzaną H₀ odrzucamy. Gdy zajdzie natomiast nierówność przeciwna | /1 < , to nie ma podstaw do odrzucenia hipotezy H₀.

Uwaga 1. Podobnie jak w modelu I, gdy hipoteza alternatywna ma postać Hi’. m₁<m₂, wtedy stosujemy w tym teście lewostronny obszar krytyczny wyznaczony nierównością tśt_t, gdzie krytyczna wartość /_a jest wtedy odczytana z tablicy rozkładu t Studenta w taki sposób, by spełniona była równość P{t^t_a} = oc. Natomiast dla hipotezy alternatywnej postaci Hi‘. mi>m₂, stosujemy w tym teście prawostronny obszar krytyczny wyznaczony nierównością />f_a, gdzie wartość krytyczna odczytana jest z tablicy tak, by zachodziła równość P {t^t_a} =a.

Należy nadmienić, że test istotności dla dwu średnich według modelu II jest ze względu na małe próby najczęściej stosowany w statystycznej analizie wyników eksperymentów naukowych z różnych dziedzin wiedzy. Nie wymaga się przy tym jednakowo licznych prób.    <

Uwaga 2. Czasem w praktyce zdar;a się, że wyniki obu prób możemy traktować jako wyniki pomiarów na tym samym elemencie populacji. Jest tak wtedy, gdy stanowią one pary przyporządkowanych sobie liczb. Typową sytuacją jest tu model: wynik x_t „przed” jakąś operacją i wynik „po” niej dla tego samego i. Ndeży wtedy analizować wyniki obu prób jako wyniki jednej próby biorąc różnice y,—a zamiast testu zamieszczo-r,eeo w modelu 11 użyć testu dla średniej różnicy-według modelu U w § 1 tego rozdziału. Stosujemy wtedy następujący wzór na wartość statystyki ł Studenta:

t = -    \ /i — 1,

5.

gdzie _>V ' ^vi- u n jest liczbą par. Zamiast hipotezy- H₀: ut_l=iu₂, weryfikujemy wtedy hipotezę //₀: Z--■=(). gdzie Z oznacza średnią w populacji różnic.

Model Tli. Mad.i my dwie populacje generalne mające rozkłady normalne In!' muc. byle <> '■!■ ^i,ii'/nineli wni iani iach o',' i oj, które są nieznane. Na podstawie wyników dwu dużych prób (n, oraz. n, >ą rzędu co najmniej kilku dziesiątków t w\|«^owanych z obu populacji należy sprawdzić hipotezę //„: m, ni, wobec hipotezy alternatywnej Hi: >n, #///,.

‘lot istotności dla sprawdzanej hipotezy //,, budujemy analogicznie jak w modelu i. tj. w oparciu o rozkład normalny .V(0, 1), z. tą jedynie różnica, że przy obliczaniu wartości u zamiast nieznanych wariancji o\ i o~₂ przyjmujemy wartości .vf i s\ uzyskane / dużych prób. , .

I*nzvki.an 1. Pragtniemy stwierdzić, czy słuszne jest mniemanie, że zatrudnione tu tyeli innych stanowiskach w pewnym przemyśle kobiety otrzymują przeciętnie niższą plącę niż mężczyźni. Z populacji kobiet zatrudnionych na określonych stanowiskach wylosowano w tym celu niezależnie próbę - 100 kobiet i otrzymano z niej średnią płacę 3ć_I = 2180 zł oraz wariancję plac vj=-=6400. Z populacji mężczyzn zatrudnionych w tym przemyśle na tych samych stanowiskach wylosowano niezależnie /t, = 80 mężczyzn i otrzymano dla nich średnią plącę as = 2280 zł oraz wariancję .vj =---10000. Na poziomie istotności u = 0,01 należy sprawdzić hipotezę, że średnie płace kobiet są niższe.

Rozwiązanie. / treści zadania wynika, że ze względu na nieznane wariancje obu populacji, ale duże próby, mamy do czynienia z. modelem III, w którym test. istotności dla sprawdzanej hipotezy jest taki sam jak w modelu I, z. tym że zamiast o\ i a\ przyjmujemy z prób wartości s* \£\.

Hipotezę badawczą o niższych przeciętnie zarobkach kobiet, zamieniamy na hipotezę statystyczną, że średnie zarobki kobiet m_t oraz mężczyzn