skanuj0004

56 II. Parametryczne testy istotności

56 II. Parametryczne testy istotności

wać w jednym doświadczeniu. Jeżeli jednak naprawdę zrealizowało to musiało mieć większe prawdopodobieństwo niż to wynika z założę., prawdziwości hipotezy J/₀, więc skłonni jesteśmy uznać hipotezę za fi szywą i odrzucamy ją. Możemy pomylić się i odrzucić hipotezę, któtj w gruncie rzeczy byki prawdziwa (błąd pierwszego rodzaju), jednak^ prawdopodobieństwo takiej pomyłki jest bardzo małe, równe obrangi dowolnie liczbie cc. Jeżeli natomiast wartość statystyki Z z próby n-elemeig towej znalazła się poza obszarem krytycznym, to prawdopodobieństwo tego zdarzenia, przy prawdziwości hipotezy JJ₀. jest równe 1— «(*), cq jest bliskie 1. Zaszło zatem zdarzenie, które powinno przy prawdziwość

hipotezy zajść, bo miało duże prawdopodobieństwo, więc nie ma podstaw do odrzucenia hipotezy i/.>.    =

Jako poziom istotności a. wybiera się najczęściej w testach istotności liczby 0,1 ()• 0,05, 0,01, 0,001, choć nie znaczy to, żc nie można wybraf np. 0,02. Oczywiście im mniejszy przyjmie sic poziom istotności w teście (czyli im mniejsze dopuszcza się ryzyko popełnienia błędu pierwszego rodzaju), tym trudniej jest hipotezę If₀ odrzucić, dlatego należy uważnie dobierać poziom istotności (najczęściej przyjmuje się a = 0,05, a mniejsze wartości przyjmuje się w wyjątkowo ważnych badaniach, np. technicznych czy medycznych). Odrzucenie sprawdzanej hipotezy na poziomie istotj ności np. 0,01 oznacza, żc odrzucając tę hipotezę albo się nie mylimy (tzn. hipoteza jest naprawdę fałszywa), albo też. popełniamy błąd pierwszego rodzaju (tzn. w gruncie r/ec/y. o czym me wiemy, hipoteza jest prawdziwa), ale w tym ostatnim przypadku częstość popełnienia takiego błędu jest tylko 1 na 100 przypadków siosnwania tego testu istotności.

Podstawą budowy obszaru krytycznego dla danego testu istotności jest rozkład odpowiedniej statystyki z próby, wyznaczony pr/.y założeniu prawdziwości sprawdzanej hipotezy o parametrze populacji.

Przechodząc do omówienia konkretnych testów istotności dla średniej wartości badanej cechy w populacji należy stwierdzić, że statystyką, której rozkład służy do budowy obszaru krytycznego w tych testach, jest średnia z próby x. W zależ,ności od posiadanych informacji o populacji wyróżnimy trzy podstawowe modele, dla których buduje się testy istotności dla średniej.

(') Nu- należy k<> mylić ze współczynnikiem ufności. Zbieżność liter i odczyty-

Model I. Populacja generalna ma rozkład normalny H(m, er), przy czym odchylenie standardowe a populacji jest znane. Należy na podstawie wyników próby losowej'ń-elemerifowej'sprawdzić hipotezę H₀: m = m₀ (gdzie m jest konkretną wartością hipotetyczną średniej) wobec hipotezy alter-

natvwncj Wj". m^nio-

Test istotności dla hipotezy //„jest następujący. Na podstawie wyników próby oblicza się wartość statystyki x, tj. średniej z próby, a następnie uartość zmiennej normalnej standaryzowanej U według wzoru

x-m₀ -

(2.2)    u-- Vⁿ-

c

Z tablicy rozkładu jV(0, 1) wyznacza się następnie taką wartość krytyczną _;, by dla założonego z góry małego prawdopodobieństwa a (poziomu istotności) zachodziła równość P {\U\^u_a}=0L (rys. 4).

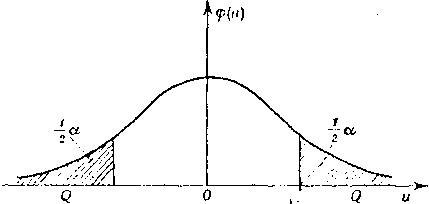
Rys. 4. Dwustronny obszar krytyczny Q

Zbiór wartości U określony nierównością | U\ jest obszarem krytycznym tego testu, tzn. gdy z próby otrzymamy taką wartość u, że |u|> ^ to hipotezę H₀ odrzucamy. Gdy zaś |m| <«„, to nie ma wtedy podstaw do odrzucenia hipotezy H₀.

Uwaga. Powyższy test z tzw. dwustronnym obszarem krytycznym stosujemy jedynie dla takiego przypadku hipotezy alternatywnej, w której występuje nierówność m^m_Q. Gdy hipoteza alternatywna ma postać H_x : m<m₀, to stosujemy test istotności z tzw. lewostronnym obszarem