skanuj0005

58 II. Parametryczne testy istotności

krytycznym określonym nierównością £/<m_s. Wtedy wartość u„ w czarny tak, by zachodziła równość P{U^u_a}=a (rys. 5).

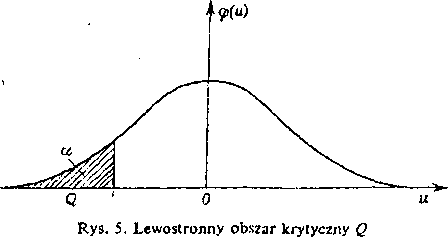
Dla hipotezy alternatywnej postaci H_x: m>m₀, stosujemy równia test istotności z tzw. prawostronnym obszarem krytycznym określonym nifcl równością {/>«„. Wtedy wartość y_a z tablicy rozkładu N(0, 1) wyznaczanfl tak, by spełniona była równość P{U^u„} = cc (rys. 6). Hipotezę //₀ odrzuj

f<p(u)

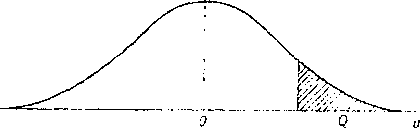
Rys. 6. Prawostronny obszar krytyczny u

cimy dla takiego przypadku hipotezy H_x tylko wtedy, gdy wyznaczona z próby wartość « spełni nierówność

Model II. Populacja generalna ma rozkład normalny N{m, a), przy czym odchylenie standardowe o populacji jest nieznane. W oparciu o wyniki malej, //-elementowej próby losowej należy zweryfikować hipotezę H₀\ m — m₀, wobec hipotezy alternatywnej H_t: m#m₀.

Test istotności dla powyższej hipotezy H₀ jest następujący. Z wyników' próby oblieza się wartość ,v oraz ,s lub s (oznaczenia jak w rozdziale 1), t następnie wartość statystyki t według wzoru

x — ni₀ - x — n i₀

(2.3)    1=............... \'u~l=—_v " •

s    s

Statssuka ta ma przy założeniu prawdziwości hipotezy H₀ rozkład Studenta o n ~ 1 stopniach swobody. Z tablicy tego rozkładu, dla ustalonego po/nunu istotności a i dla n — 1 stopni swobody, odczytuje się taką wartość /,, Lc P{’h3=Nierówność \t\^t_a określa obszar krytyczny (dwustronny) w tym tekście. Wystarczy więc porównać obliczoną z próby według wzoru (2.3) wartość zmiennej t z wartością krytyczną t₃, odczytaną z tablic rozkładu Studenta, .leżeli zajdzie nierówność    to hipotezę H₀

należy odrzucić na korzyść hipotezy //,, natomiast gdy zajdzie nierówność przeciwna |r|</,, to nie ma podstaw do odrzucenia hipotezy tlili w a g a. Gdy hipoteza alternatywna H_x jest w postaci nierówności m<»/₀, to podobnie jak w modelu 1, stosuje się wtedy w tym teście obszar krytyczny lewostronny, tj.    wyznaczony tak, by    Nato

miast gdy alternatywna hipoteza H_x jest w postaci nierówności m>m₀, to stosuje się w tym teście obszar krytyczny prawostronny określony nierównością    przy czym t_x wyznacza się w taki sposób, by zachodziła

równość /’ \t■ i, | v (por. rys. 5 i 6 dla testu U).

Model 111. Populacja generalna ma rozkład N(m, o) lub dowolny inny rozkład o średniej wartości ni i o skończonej, ale nieznanej wartości wariancji n-. Na podstawie wyników dużej próby losowej (n co najmniej rzędu kilku dziesiątków) z. tej populacji należy zweryfikować hipotezę ł!_t): ni-- /u,,, wobec hipotezy alternatywnej //,:

Test istotności dla tej hipotezy jest analogiczny jak w modelu I, tzn. jest testem U, z tą tylko różnicą, że zamiast wartości a przyjmuje się wyznaczoną z dużej próby wartość ,v.

Pr/, ykt ar> 1. Pewien automat w fabryce czekolady wytwarza tabliczki czekolady o nominalnej wadze 250 g. Wiadomo, że rozkład wagi produkowanych tabliczek jest normalny N(m, 5). Kontrola techniczna pobrała