img040

8S II. Parametryczne testy istotności

2.6. TEST DLA DWÓCH WARIANCJI

Podstawowe wyjaśnienia

W przypadku gdy badanie statystyczne 2e względu na pewną cechę mierzalną prowadzimy w dwóch populacjach, może zajść potrzeba sprawdzenia hipotezy o jednakowym stopniu rozproszenia wartości badanej cechy w obu populacjach. Gdy populacje mają rozkłady normalne, można tę hipotezę łatwo sprawdzić podanym poniżej prostym testem istotności.

Najczęściej podany tu test służy jako sprawdzenie założenia wymaganego przy teście r Studenta dla dwu średnich (por. § 2 tego rozdziału). Założenie występujące tam dotyczy właśnie równości wariancji w obu populacjach, których średnie chcemy porównać.

Rozkładem, którym będziemy posługiwać się w omawianym teście, jest rozkład F Snedecora. Ze względu na to, że dostępne tablice tego rozkładu zostały sporządzone tak, iż podają taką wartość F_vt dla której zachodzi równość F{F^F_a}=ot, w omawianym teście obszar krytyczny jest prawostronny. Dlatego oznaczenia populacji numerami 1 i 2 należy tak przyjąć, aby w ilorazie dwu wariancji z prób ticznik był 2awsze większy od rniaDOwnika. Przy odczytywaniu z rozkładu F Soedecora wartości krytycznej F_m dla tego testu należy pamiętać, że występują w nim dwa rodzaje stopni swobody — licznika i mianownika, prz^ czym w tablicach tego rozkładu w główce umieszczone sa stopnie swobody licznika, a w boczku stopnic swobody mianownika.

Ze względu na to, że w omawianym teście wygodniej jest używać statystyki

r=-

jako estymatora wariancji a², io w przypadku gdy obliczono wartość statystyki

s²=— I (x -x)²,

n i-i

przekształcamy ją na wartość 5 ² według wzoru

(2.9)

s²=-

n —1

Model* Dane sa dwie populacje generalne mające odpowiednio r02-kłady normalne N(m₃,/7_s) i A'(tft₂,<r»), gdzie parametry tych rozkładów są nieznane. Z populacji tych wylosowano niezależnie dwie próby o liczebności edpowiedruo n, i «_s elementów. Na podstawie wyników tych prób należy sprawdzić hipotezę //_c: at = crl, wohec hipotezy alternatywnej //i: <*] ><*i-

Test istotności dla tej hipotezy jest następujący. Z obu prób wyznaczamy wari ości $7 i s>, przy czym s;>9j. Z kolei wyznaczamy według wzoru

(2.10t

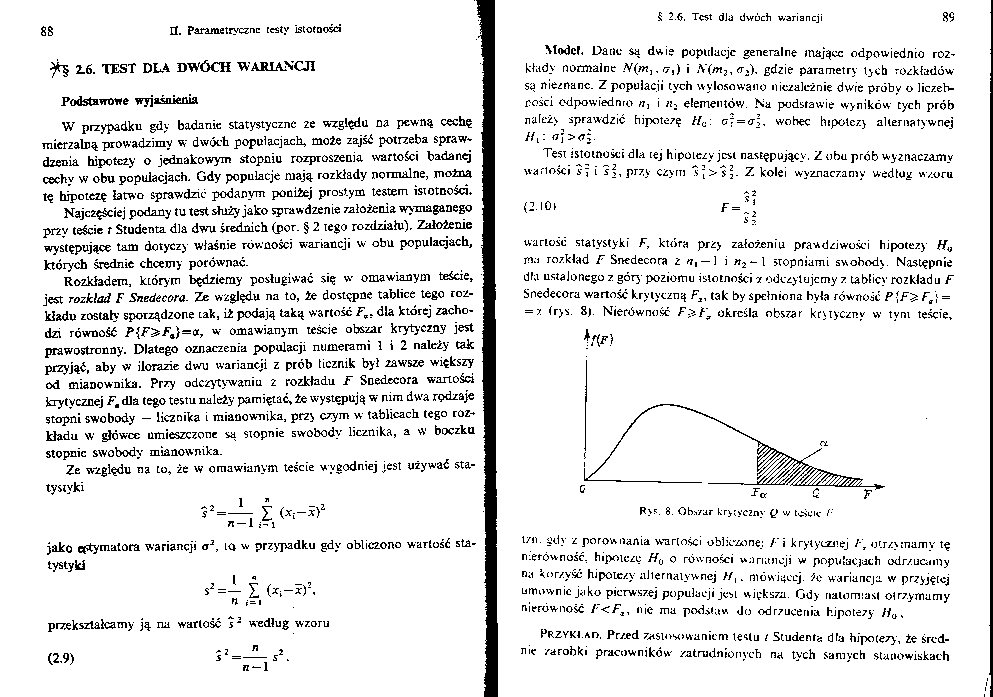
wartość statystyki F, która przy założeniu prawdziwości hipotezy ff_Q rna rozkład F Snedecora z ^, — 1 i n₂-\ stopniami swobody. Następnie dfa ustalonego z góry poziomu istotności -/ odczytujemy z tablicy rozkładu F Snedecora wartość krytyczną F₂, tak by spełniona była równość P\F^ F_a\ = = z (rys. 8j. Nierówność    określa obszar krytyczny w tyni teście*

C

R>f=. o. Ob.i/ar krytyczny Q w teście /'

t/n. gdy z porównania wartości obliczone: fi krytycznej F_r otrzymamy tę nierówność, hipotezę H₀ o równości wariancji w populacjach odrzucamy na korzyść hipotezy alternatywnej //, * mówiącej, że wariancja w przyjętej umownie jako pierwszej populacji jest większa. Gdy natomiast otrzymamy nierówność F<F_Z, nie ma podstaw do odrzucenia hipotezy Ji_0s

Przykład. Przed zastosowaniem testu t Studenta dfa hipotezy, że średnie zarobki pracowników zatrudnionych na tych Samych stanowiskach