L3 s1

Wydział BLiW Ćwiczenia rachunkowe

Lista 3

Energia kinetyczna l praca. Energia potencjalna i zasada zachowania energii.

Zadanie l

Śmigłowiec wyławia i oceanu ostronautkę o masie 72 kg, wciągając ją za pomocą liny na wysokość iS m, Astronaulka porusza się przy tym z przyspieszeniem g/10. Jaką pracę wykona nad astronautką; (a) siła przyłożona ze śmigłowca; (b) działająca na nią siła ciężkości? Ile wynosi w chwili dotarcia astroneutkl do śmigłowca jej: (a) energia kinetyczna; (b) prędkość?

Zadanie 2

Pocisk o masie 30 g lecący poziomo z prędkością 500 m/s zagłębia się w ścianę na głębokość 12 cm. (a) Ile wynosi przy tym zmiana Jego energii mechanicznej? (b) Ile wynosi średnia wartość siły hamującej działającej na pocisk ze strony ściany?

Zadanie 3

Podczas lawiny kamiennej nieruchomo początkowo blok skalny ześlizguje się po zboczu o długości S00 m ł wysokości 300 m. Współczynnik tarcia kinetycznego między blokiem a zboczem wynosi 0,25, (a) Przyjmując, że energia potencjalna układu blok-Ziemla jest równa zeru u podnóża stoku, wyznacz wartość energii potencjalnej przed ześlizgnięciem się bloku, (b) Ile energii zostaje zmienione w energię termiczną w czasie ruchu bloku? (c) Ile wynosi energia kinetyczna bloku u podnóża stoku? (d) Jaką ma on wtedy prędkość?

Zadanie 4

Sanki ześlizgują się z pagórka, którego zbocze ma długość d = IOm i jest nachylone pod kątem a = 30° do poziomu. Jaką odległość x przebędą sanki na odcinku poziomym po zjechaniu ze zbocza, jeżeli na całej drodze współczynnik tarcia wynosi / = 0,2?

Zadanie 5

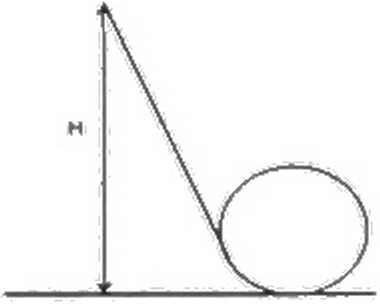
Z jakiej minimalnej wysokości H powinna się toczyć bez poślizgu mała kulka aby nie oderwała się w najwyższym punkcie „diabelskiej pętli" o promieniu r = 20 cm. Jaką prędkość ma kulka w tym punkcie?

Zadanie 6

Wartość prędkości początkowej kamienia rzuconego ukośnie jest 5 razy większa od jego prędkości w najwyższym punkcie toru. Pod jakim katem wyrzucono kamień?

Zadanie 7

Oblicz średnią moc silnika samochodu o masie 1000 kg, który poruszając się ruchem jednostajnie zmiennym w ciągu czasu 10 s od początku ruchu zmienił prędkość od 0 km/h do prędkości 50 km/h. Współczynnik tarcia wynosi 0,01,

Zadanie 8

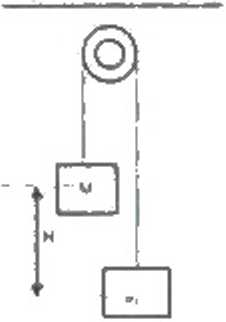
energii środek a nić m_t jeśli

Dwie masy m i M (patrz rysunek obok) są połączone nieważką nicią przewieszoną przez nieważki krążek. Stosując zasadę zachowania mechanicznej wyznaczyć prędkość V masy m w momencie, gdy jej masy podniesie się na wysokość H. Założyć, że krążek nie obraca się, ślizga się po jego powierzchni bez tarcia. Jaka będzie ta prędkość ciała odstąpimy od założenia o Idealnie gładkiej powierzchni krążka 1 przyjmiemy, że na drodze H praca sił tarcia będzie równa IV?