3818437861

Wydział BLiW Ćwiczenia rachunkowe

Lista 4

Kinematyka i dynamika bryły sztywnej. Zasada zachowania momentu pędu.

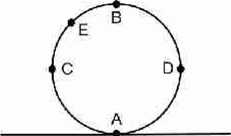
Zadanie 1

Koło toczy się bez poślizgu ze stałą prędkością liniową v₀ po prostym odcinku drogi. Znaleźć chwilowe prędkości punktów A, B, C, D, E leżących na obwodzie koła względem ziemi.

Zadanie 2

Jaką siłą należy przycisnąć klocek hamulcowy do powierzchni koła rozpędowego o momencie bezwładności I i promieniu R, aby zatrzymać je po upływie czasu t, jeżeli wiruje ono z prędkością kątową Do? Współczynnik tarcia wynosi f.

Zadanie 3

lo

Dwa odważniki o masach mi = 2kg, m2 = 1kg są połączone nicią przerzuconą przez krążek. Promień krążka R = Q,1m, a jego masa m= 1kg. Obliczyć:

a)    przyspieszenie a z jakim poruszają się odważniki,

b)    naciągi Fi i F-jnici, na których są zawieszone odważniki.

Krążek uważać za jednorodny, a tarcie pominąć.

Zadanie 4

Szpulka, podobna do zabawki jo-jo, składa się z dwóch jednorodnych krążków o równych masach M i o promieniach R oraz łączącego je wałka o promieniu r i o masie, którą można pominąć. Na szpulce nawinięta jest nić przyczepiona do sufitu. W chwili początkowej pozwalamy szpulce, spoczywającej w odległości D od sufitu, swobodnie opadać w dół. Z jakim przyspieszeniem porusza się do dołu środek szpulki?

Zadanie 5

Kula o masie M i promieniu r stacza się (bez poślizgu) po równi pochyłej o długości d i kącie nachylenia a. W chwili początkowej kula znajduje się w spoczynku. Oblicz wartość prędkości liniowej środka masy kuli przy podstawie równi.

Zadanie 6

Cienki pręt o masie M i o długości L spoczywa na gładkiej poziomej powierzchni. Mały kawałek kitu również o masie M, poruszający się z prędkością v w kierunku prostopadłym do pręta uderza w jego koniec i przykleja się do niego. Zderzenie (niesprężyste) trwa bardzo krótko.

(a)    Jaka jest prędkość środka masy układu przed i po zderzeniu?

(b)    Jaka jest prędkość kątowa układu (względem środka masy) tuż po zderzeniu?