018

Ciągłość funkcji w punkcie

Sprawdzamy, czy zachodzi równość: lim/(x) =/(x)

■'-“o

lim/(x) = ^ =/(l)

A->l    2

Odpowiedź

Funkcja/jest ciągła w punkcie x₀ = 1

ZADANIE 5

Sprawdź, czy funkcja /'jest ciągła w punkcie x₀, jeżeli:

/(+) =

3.r² + 2 5x² + 3 ’

-1.

Rozwiązanie:

Założenia: 5x² + 3^0, czyli x e R

Najpierw liczymy wartość funkcji/w punkciex₀ = -1

f(x₀) =/(-!) =

3 (— 1 )² + 2 5(-l)² + 3

3 + 2    5

5 + 3 “ 8

5

8

Czyli /(-1)

lim /(x) = lim

Teraz znajdujemy granicę funkcji /'w punkcie x₀ = -1 3x² + 2    3 (— 1 )² + 2    3 + 2    5

a->-i 5x² + 3    5 (— 1 )² + 3    5 + 3    8

Czyli lim f(x) = f

-V—1    O

Sprawdzamy prawdziwość równania: lim/(x) =/(x )

v— lim/(x)=|=/(-l)

x—>~1    o

\mm >Aj

Ciągłość funkcji w punkcie

Odpowiedź

Fu n kej a/(x) jest ciągła w x₀ = -1

ZADANIE 6

Sprawdź, czy funkcja/jest ciągła w punkcie x₀ Jeżeli:

m=

4-x

x² + 2 ’

4

Rozwiązanie:

Założenia: x^:+ 2 * 0, czyli x e R

Najpierw liczymy wartość funkcji/w punkcie x= 4

A\) =7(4) =

4-4

4² + 2

0

16 + 2

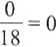
Czyli /(4) = 0

Teraz znajdujemy granicę funkcji/w punkcie x₀ = 4

0

4-x 4-4    0

lim f(x) = lim ——- = ——— = —

'⁷ v x-,4 x² + 2    4^: + 2    18

Czyli lim f(x) = 0

A->4

Sprawdzamy prawdziwość równania: lim f(x) = /(x ). Zatem:

^x~*^xo

lim/(x) = 0 =/4)

.v->4

Odpowiedź

Funkcja/jest ciągła w punkcie x₀ = 4

ZADANIE 7

Sprawdź, czy funkcja/jest ciągła wx_Q, jeżeli:

a \ ^{4x + 3}    ,

f(^x) = -JZJ’ ^xo ⁼ 1

35