0000134

Dlo dowodu twierdzenia Lantleri-Tronto potrzebno będę Joez-cze jako lematy dwa twierdzenia znono w toorii macierzy i

L e ■ e t 0.3.5

Oożeli w noclerzy kwodratowoj okroślonej nod piorścieniem Z liczb całkowitych zraionley znok dowolnego clomontu, to porzyo-tość względnie* nieporzyotość wartości jej wyznoczniko nio ulegnie zmianie.

Lemat 0.3.6

Niech moclerz kwadratowa będzie okroślona nad piorścieniem Z liczb całkowitych, a jej elementy maję wartości ze zbioru |-1 . 0, i) . Dożęli każdo kolumno zowiore dokładnie dwa niezo-rowe elemonty o różnych znokach (-1 i 1), to wartość wyznacznika tej macierzy należy do zbioru {-1.0,1 } .

Dowód twierdżenio Lonticri-- T r e n t a

Mamy wykazać, żo ilość różnych korkaoów grafu C ■ <X,U,P> Jest równa minorowi głównemu rzędu <J>(G) maciorry S(G) •

* (*ij]n*n '    " *    • «^drl*

2 •(x₁) • r(x₁) dla i - j

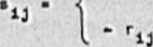
powstałemu przoz wykriślonio X wierezy i tych eomych kolumn, odpowiadajęcych wierzchołkom, wziętym dowolnie po jednym z każdej okładowej opójneści grafu G.

Wystarczy zotea wykazać, żo (patrz wnioaek 5) wortość togo ■ inora jeot równe ilości niezerowych ainorów rzędu ę>(G) macierzy A°. przy uotalenym pedzbiorze liniowo niezależnych wierszy

{ *1.....^łf) *

Ilość tych niezerowych minorów wyznaczymy wprowadzojęc maciorz o elementach identycznych jak mocierz A^ . lecz określono nad pierścieniem liczb całkowitych.

Dowolny minor macierzy A° jeot zerowy wtedy i tylko wtedy, gdy minor ton w macierzy A^Z ma wartość parzysto. Korzyatajoc z lematu 0.3.5 zaetopiey macierz A** macierzo A*" utworzony w ton epooób, Zo w koźdoj kolumnie macierzy A ² zo-mlenimy Jedoń z dwóch olocontów o wortodci_l no olonont o wor-todci -1. Doatojomy w ton opooób mociorz A² , o któroj bowo w lonoclo 0.3.6. Zouwożmy, lo wortoócl bezwzględno elnorów odpowiadających oobio w mociorzoch A° i A^Z będę idontycznlo (0 lub l). Zotoe dowolny podzbiór kolumn mociorzy A° Joot podzbiorom kolunn liniowo niezależnych wtody i tylko wtody, gdy ton oom podzbiór kolumn aocierzy A^Z joot podzbiorom kolumn liniowo niozolożnych. Ooźoli toraz utworzymy aaciorz S ■ A^Z( A^Z)^T» T - znok troneponowania macierzy, to z rachunku mociorzowogo v/indomo, żo wortoóć głównego minoro mociorzy S . utworzonego

przoz ę(G) wiorazy i tych aamych kolumn o numorach i₁.....^lQ{G)'

będzio równa eunlo kwadratów wortoócl wazyotklch minorów rzędu f(G) tworzonych przoz wiorozo i_1#...,ięj_cj maciorzy A². Uwzględnlojęc Jodnok, że minory mociorzy A**    wortoócl

bozwzględno O lub 1 (ich kwodraty toż sę równo O lub 1), otrzymujemy wnlouok, że wartodć omowlonogo minoro, głównego mocio -rzy S Joct równo iloócl nlozarowych minorów mociorzy A² , o więc i mociorzy A°, tworzonych przoz wybrane wiorozo o numo -rach i_1#...,ię/_Cj» a o to władnie nam chodzi (patrz wnioakl 3,

■4 15).    *

Ola zakończania dowodu wyatorczy tylko wykezać, żo macierz S • A^( A^Z)^T joot równo mociorzy S okrodlonoj w twlordzoniu Lentiorl-Trenta. Woźmy w tym celu pod uwagę ozneczenlo S •

[°ij]nx.n ' A ■ [^ij]_n*m *

Otrzymamy    ,

" £? **^r **^r

Rozwoźmy jokio wortoócl przyjmuję elementy e_iJf W każdej kolumnio A² reprezentujęcoj krawędź u^ oę dwo olemonty nlozorowo (-1 i 1). Wyotępuję one no przecięciach z wiorazomi reprezentu-Jęcyoi wlorzchołkl grafu lncydentne z krawędzią u^. Zetom ele -nent e^ dlo i ■ J jeat dodatni i równy lloóci krowędzl incydon-tnych z wiorzchołkloB o numerze 1. Notomioet dla i / J, element *1J J^08t morowy lub ujemny, o Jogo wortoóć bezwzględna Jeat równa iloócl krowędzl łączących wierzchołki i-ty i J-ty (iloczyn ekolarny dwóch wierozy i-togo i J-togo macierzy A²).

267