046(1)

Różniczkując pochodną y', mamy

(/)' = y" = 20x* — 42.v Różniczkując drugą pochodną y", znajdujemy

(/')' = /" = 60.y²^42

2) Pierwsza pochodna

y' = (ln x)' =    = x~^l

Aby ułatwić wyznaczenie następnych pochodnych wprowadziliśmy ujemny wykładnik potęgi; mamy

24

y"=-*-²;    y"' = 2*-³;    /» =-6x~⁴;    /» = 24x~> =-

3) Wyznaczamy kolejno odpowiednie pochodne

_S'-(arc.g2.«y = _t2A)₂₌_A_.

s =

2(1+4^)'

(1+4^)²

16.*

(I+4?f

16 25 ’

Dla x = — 1 znajdujemy $"(—!) =

4) Znajdujemy y' i y"

y' — sin <jp-i-e^_‘^?’(sin 9")' = —e~'* sin <p-\-e~^v cos <p = e~^lf(cos(f—sin(f) y" = — e~^ę(coś<p—sin 9?)-ł-e^_ę,(—sin 9?—cosf) = —2e~'^l’cos<p Podstawiając y, y i y" do danego równania, otrzymamy tożsamość —2e^_,’coS95+2e^_'^?(cos9?—sin (y)-[-2(?^_,,’sin <p = 0;0 = 0 4) Stosując wzór Leibniza, otrzymamy

y^<24) = [e^x(x²—1)]⁽²⁴> = (e^x)(²⁴)(x²~ l)-j24(e^x)⁽²³⁾(.r^!—1)'+

+ -

24 • 23

Wszystkie pozostałe składniki są równe zeru, ponieważ wszystkie pochodne funkcji x²--l rzędu wyższego niż drugi są tożsamościowe równe zeru. Zatem

y⁽²⁴⁾ = _e^x(x¹-l)+24e^x ■ 2x+l2 ■ 23e^x ■ 2 = e^x(x²+48x+551) (gdyż pochodna dowolnego rzędu funkcji e^x jest równa e^x)^

6) Różniczkując A-krotnie, otrzymamy

y = _x^m, y' = mx^m-\ y" ----- m(m-l)*^m-²,    ,

y<*> = m (m - 1)... (m - A + 1

W szczególności, jeżeli m jest liczbą całkowitą dodatnią, to

y(n<) — _m\ j j,(ml i) _ y(m\2) _    _    _ Q

Wyznaczyć pochodne wyższego rzędu dla funkcji:

217.    z = f²+sin5f; wyznaczyć z"'

218.    v = a⁵ ln a; wyznaczyć v"'

219.    x — (2p— l)⁵; obliczyć x^(4,(3)

220.    y — x²e^3x; wyznaczyć y"

221.    y = c₁e²*-fc₂Ae^2l+e^I; wykazać, że funkcja ta spełnia równanie y"—4y'-f 4y = e*

222.    y — a^2x; wyznaczyć y⁽ⁿ⁾

d^ky

223.    y = (1 +x)^m; wyznaczyć jj_xk

.    , d^I0y

224.    y = x sin x; wyznaczyć

225*. y = a"^-1 ln x; obliczyć y^(n,(l)

§ 9. Pochodne funkcji uwikłanej

Jeżeli y jest funkcją uwikłaną x, tzn. jeżeli zależność y od x jest dana równaniem f(x, y) — 0 nie rozwiązanym względem y, to w celu znalezienia

pochodnej ^ należy zróżniczkować względem x obie strony równania,

pamiętając, że y jest funkcją ,v, a następnie rozwiązać otrzymane równanie względem poszukiwanej pochodnej. Będzie ona na ogół zależeć od x i y;

<ly ,    .

Drugą pochodną    funkcji uwikłanej otrzymamy przez zróżniczkowanie

funkcji (f (x, y) względem x, przy czym należy pamiętać, że y jest funkcją x

dy ₌ d<p{x,yf dx² dx

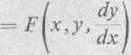
95