Pochodne fukcji rozniczkowalnosc zadg 84 odpowiedzi

KK1H0DNH rUNKCR tUMNICZKOWALNOSC
Podobnieapnwdzuny.że/'j = -x. Zatem /nic jest ró/nictl^fl w zbiorze {jc4: k ■* 0, ± 1, ± 2,...}, który ma własność wskazany w tekście
A2sin^
68. Mamy: /'(O) = lim —-— = lim A sin ^ = 0 oraz f'(x) m 2Jtł»'
eos - dla x # 0. Ponieważ lim/'(x) nie istnieje (dlaczego?), więc / nu- (* ciągła w punkcie x = 0.
69- f'(xo)- Z istnienia powyższej granicy i Pokazuje to przykład funkcji (0 dla x?t0 /W-jl dla x = 0,
70. a - -2, b--12. / nie jest różniczkowalna.
72. o - % b - 0.
n f'Q+). (Stm, ,im
/•(o-)- lim _ lim
W *-0- X2
Zatem / nie jest różniczkowalna w punkcie x = 0.
75. /'(0+) = /'(0-) = — ^, a więc/'(0) nie istnieje.
76. Przedstawiając/(x) = - — ^ cos 2x otrzymujemy, że /**(*) - -2"_,cos^2x+ ~V
77. Wskazówka: Przedstawić f(x) w postaci: f(x) = - t ^ cos 4«
• 0. , ję,- -Vix‘-y')-
-hv (**—>*) .= -- J
v'(y) + . Zalo/cmu Czyi'
•I . fl.l2,,, ,V** d<t, df 3ftw
z twierdzenia 0 różniczkowaniu fankcji ilożonytli
Kierunkiem tym jest gradient funkcji/(x, y) - x* + yłł 1»y w punki O lufy jest równy (5,5). Zatem spadek powierzchni w kierunku dwu»u>i n *,,r' ^w'ar*ki płaszczyzny xOy będzie największy.
**' ^cfsor u, o którym mowa w zadaniu, ma postać i
• = COS ot + sin a. Łatwo pokazać, że max - j. -y ) (dlaczego?)
M. Weźmy niezerowy wektor u = (u,, u2). Wtedy /■(0,0) . Um/^bAM , iint/J^! -
.lim
I «o l(tłut + /2u!) u} + ul '
...... .tcżcsóiności « = !H = I
ox oy
t (dyby / była różniczkowalna w punkcie (0,0), to istniałaby funkciii r (li,
• >%* te lim 'IV^ _ o i taka, źe f(ht, hx) = r(h|t hx) dla dowoln<
l+Ę
ik, li,) Stąd mamy:
r(fc„h,) hthl _0
lim — - lim U’
|i «l nieprawdą. Rzeczywiście, biorąc ciąg I
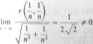
Wyszukiwarka
Podobne podstrony:
Pochodne fukcji rozniczkowalnosc zadg 84 odpowiedzi Podobniesprawdzamy,że/ ~ J = -lt ^tcm/nicjest ró
Pochodne fukcji rozniczkowalnosc zadI 67 odpowiedzi HiaiODNI HIHKCJi *A*NK7IIOWMNO*X^m ^xrT7+T1 0 /
Pochodne fukcji rozniczkowalnosc zad 8 49 odpowiedzi H H INKCJI Rrt*Nli /KOWAI NOftfK. / (3) rl«. /
Pochodne fukcji rozniczkowalnosc zad 1 7 odpowiedzi **• Niech AcX, A * 0, A =A. Weźmy yef(A). Wtedy
Pochodne fukcji rozniczkowalnosc zad 1 7 odpowiedzi 88. Niech AcX, A * 0, A = A. Weźmy ycf(A). Wtedy
Pochodne fukcji rozniczkowalnosc strt 75 Rozdział VIIIPOCHODNE FUNKCJI. RÓŻNICZKOWALNOŚC Część A 1.
Pochodne fukcji rozniczkowalnosc strv 77 76 76 38. h (m) = 3”". 40. g (x) = V cosh x 42. Oblicz
Pochodne fukcji rozniczkowalnosc strx 79 Część B 62. Zbadać różniczkowalność funkc
Zgromadzenie odpowiednich dowodów W pracy musimy udowodnić, że nasze stwierdzenie jest słuszne przy
DSC08090 (2) IstoUu różnica między baśnią a bajką polega także na tym, że celem bajki jest przede ws
1 Wpisz odpowiednie liczby w pustych polach wiedząc, że w wyróżnionym kółeczku jest wynik dodaw
Nartowska Różnice indywidualne0033 nie pochodzenia środowiskowego. Krótkie i zwięźle sformułowane od
Skrypt PKM 1 00042 84 84 Odpowiedź: * s - Iha_ fs3 22h3a + 3haT+2a5 l>h. Zadan
page0092 84 Summa teologiczna w jej naturze, tak, że słusznie jedno należy do dn;a, a drugie do wiec
więcej podobnych podstron