Pochodne fukcji rozniczkowalnosc strx 79

Część B

62.    Zbadać różniczkowalność funkcji /(x) = |x|³ na zbiorze SL

63.    Pokazać, że funkcja

_ fx² dla x wymiernych (0 dla x niewymiernych ma pochodną tylko w punkcie x = 0.

64.    Niech /(x) = cos (sin ^/T). Obliczyć lim /'(x).

65.    Niech / (x) =    Obliczyć lim (x —2)²/'(x).

66.    Zbadać różniczkowalność funkcji / (x) = _v/sinx².

67.    Pokazać, że funkcja

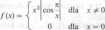
ma tę własność, że w każdym otoczeniu punktu 0 znajdują się punkty, w których funkcja ta nie jest różniczkowalna. Ponadto pokazać, że / jest różniczkowalna

68.    Obliczyć pochodną funkcji /: 51 -* IR, gdzie

^dla

L 0 dla x = 0.

Czy /' jest ciągła na IR?

f(x₀ + h)-f(x₀-h) >    2/i

69.    Zakładając, że funkcja / jest różniczkowalna w punkcie x₀, obliczyć granicę

Czy z istnienia powyższej granicy wynika, że /' (x₀) istnieje?

70. Niech/:&-+!&,

dla x < —2 dla —2 < x < 3

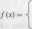
3—x dla -2«£: r² + x+ł> dla 3<x.

Dobrać a i b tak, żeby funkcja / była ciągła na ift. Czy ta funkcja jest różniczkowalna na IR?

71. Niech /:id -*R będzie określor

/(*)«

x + a    dla x < - 1

- bx² +2    dla — I < x < O

ccosx + d dla 0<x<~

^</p“”‘+p—1 dla x >

Dobrać parametry a, b, c, d. p tak, żeby ta funkcja była różniczkowalna na R.

72. Niech /:R -»R będzie określona w następujący sposób

I tlą jakich wartości a i b funkcja ta jest różniczkowalna na R?

x > -1.

w 73. Zbadać, czy funkcja /(x) = ^/lnfl +x²) jest różniczkowalna w punkcie

(•O.

L 74. Niech/:R-R,

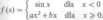
Dobrać u i b tak, żeby / była wszędzie różniczkowalna.

75.    Zbadać, czy funkcja /: R -* R, określona w następujący sposób

Jxarctg- dla x^0

I    ” I 0 dla x - 0,

lim pochodną w punkcie x = 0.

76.    Wyznaczyć f^im){x), jeśli f[x) = sin^Ix.

'    77. Wyznaczyć (x), jeśli /(x) = sin⁴x+cos⁴x.

7X. Niech <p będzie funkcją różniczk owalną na UL Pokazać, że funkcju • y <p(x^ł -y^J) spełnia równanie różniczkowe

I dz I dz z

79. Pokazać, że jeśli funkcja ę>:R-»R jest różniczkowalna, to funkcji