109(1)

r p (X)

Całkę _n. dx wymiernej funkcji ułamkowej, gdzie P (x) i Q (x) są j y i*)

wielomianami, można obliczyć (czyli wyrazić przez funkcje elementarne) przez rozkład jej na sumę całek, z których każdą, w wyniku dalszych przekształceń, sprowadza się do wzorów podstawowych rachunku całkowego.

Jeżeli dana funkcja wymierna stanowi ułamek niewłaściwy, czyli jeżeli stopień licznika jest wyższy lub równy stopniowi mianownika, to przez podzielenie licznika przez mianownik sprowadzańiy ją do sumy pewnego wielomianu i ułamka właściwego wy miernego, w którym już stopień licznika jest niższy od stopnia mianownika.

Z kolei ułamek właściwy wymierny można zawrze przedstawić jako sumę ułamków prostych o postaci

A    _r _ Mx+N

(x—a)^m °^raZ {x^1Jrpx-\-q)ⁿ

(m i n — liczby naturalne), które są już całkowalne.

X(x)

Rozkład ułamka właściwego wymiernego ^^yna ułamki proste przeprowadzamy w następujący sposób:

a)    Rozkładamy mianownik Q(x) na czynniki proste rzeczywiste. W ogólnym przypadku, na podstawie zasadniczego twierdzenia algebry, w rozkładzie tym będą występowały czynniki liniowe i kwadratowe

0(x) = (x—a)^m ... (x—b)^k ■ (x²-px \ q)ⁿ... (x^ljrcx - dy

b)    Piszemy ogólny schemat rozkładu danego ułamka na ułamki proste. Będzie on miał postać

^ (*) A t    i A 2 ,    , A m

Q(x)    x—a (x—a)²    1 (x—a)^m

,    ^2    ,    , Bk ,

•••⁺    +    + •” ⁺ (x-bj ⁺

_ ¥, x+Nj    M₂x+N₂    ^ M_nx+N_n _

x^lJrpx+q ' (xⁱ+px+q)^z '    (x^z+px+q)^H

C| x-f-D| ₍ _C₂ x^J_rP₂_ ^    ___C, x— D_r_

x^Zjt-cx-\-d (x?-\-cx-\-d)²    1 (x^zĄ-cx-\-d)^r

gdzie współczynniki A_u    B_u    N_lrC_u D_u ... są pew

nymi stałymi, które należy wyznaczyć. W schemacie powyższym dla każdego czynnika z rozkładu mianownika 0(x) wypisujemy tyle ułamków prostych, ile wynosi krotność (m, k, n. r, ...) danego czynnika.

Mianownikami ułamków prostych będą kolejne potęgi o wykładnikach naturalnych każdego z czynników rozkładu Q(x), poczynając od potęgi pierwszej, a kończąc na potędze wjakiej czynnik ten występuje w rozkładzie Q(x),

Licznikami ułamków prostych będą bądź stałe A,. A_z, .... bądź też funkcje liniowe M_vx+N_lt ... w zależności od tego, czy mianownik jest potęgą czynnika liniowego, czy też potęgą czynnika kwadratowego.

c)    Traktujemy wypisany rozkład jako tożsamość i uwalniamy się od mianowników mnożąc obie jej strony przez Q(x).

d)    Przyrównujemy współczynniki przy jednakowych potęgach x po obu

stronach tożsamości; dostaniemy wtedy układ równań, w którym niewiadomymi będą A_u ..., B_t,.... M_u ..., N_t, ..., Cj,    ... i w którym liczba

równań będzie równa liczbie niewiadomych.

e)    Rozwiązujemy ten układ równań i znalezione wartości A_u ..., B_1} ..., M_u ..., Nu .... C_u podstawiamy do schematu rozkładu.

Po rozłożeniu na sumę ułamków prostych, całkowanie każdej właściwej funkcji wymiernej sprowadza się do obliczenia całek typu

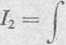
MxĄ-N

\xⁱ+px+q)ⁿ

I f dx ¹ J (x-a)^m

Pierwszą całkę, gdy m ^ 1, oblicza się ze wzoru 1

(x—d)~^m+i —m+1

a gdy m = 1, ze wzoru 2

r dx

'    — = ln x—a A C

J x-a

Całkę h, gdy n = ł, można obliczyć na podstawie reguły podanej w § 5, a gdy n — 2,3,4,... przez zastosowanie przekształceń omówionych przy rozwiązywaniu poniższych zadań.

526. Obliczyć całki:

•>/

³⁾J

3^+8

xⁱ+4xm-4x^dX

xⁱĄ-4x²—2x+l

*⁴+x

dx ■

r 2x⁵+6xⁱ-h1

²)J-?+3sr*

41 f (x?-3)dx ^JJ x⁴+10^+25

221