5806256272

Część III: Termodynamika układów biologicznych

gdzie L, M, N są pochodnymi cząstkowymi funkcji g odpowiednio po x, y i z:

L = —	L = —	L = —
<3x	3x	dx

Ostatecznie różniczka parametru (zmiennej stanu) g przyjmuje postać:

_dg=®Łdx-3_dy+08_dz

dx ty cz

Funkcje stanu

Jeżeli wartość pewnego parametru nie zależy od drogi, po jakiej została osiągnięta, a jedynie od stanu układu, to parametr taki nazywamy funkcją stanu. Opis stanu układu przy pomocy funkcji stanu ma szereg zalet. Przede wszystkim:

■    wartości funkcji stanu w stanie równowagi termodynamicznej zależą tylko od parametrów zewnętrznych, czyli dających się zmierzyć

■    wartości funkcji stanu w dowolnym stanie można obliczyć korzystając z różniczki tej funkcji. Istnieje prosty sposób ustalenia, czy dany parametr jest funkcja stanu korzystając z równania stanu. Można wykazać na gruncie rachunku różniczkowego, że w przypadku funkcji stanu jej różniczka musi być tzw. różniczka zupełna. Różniczkę nazywamy zupełną jeżeli dla każdej pary parametrów x i y zachodzi równość:

lilii)

dy dx

Sprawdźmy, czy objętość jest funkcją stanu gazu doskonałego. Przekształćmy najpierw równanie stanu gazu doskonałego tak, aby dla 1 mola gazu uzyskać zależność objętości od ciśnienia i temperatury:

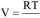
P

Wyznaczmy teraz różniczkę objętości:

... dV._ av.    R._ RT.

dV = —dT + — dp = —dT _rdp

oT    dp    p    p

i sprawdźmy czy jest to różniczka zupełna:

JdV)		/r) / RT'|
		%J Vp-J
dp	dr	dp dr

_R

P²

R_

P²

3