5806256273

Część III: Termodynamika układów biologicznych

Tak więc objętość jest funkcją stanu gazu doskonałego. W analogiczny sposób można wykazać, że temperatura i ciśnienie są również funkcjami stanu gazu doskonałego.

Sprawdźmy teraz czy praca mechaniczna wykonywana przez gaz doskonały jest funkcją stanu tego gazu. Najpierw musimy znać różniczkę pracy gazu doskonałego. Z fizyki i chemii fizycznej wiemy, że różniczka pracy równa jest:

dW = -pdV = -pf — dT - dpi = -RdT +—dp kP P ) P

Sprawdźmy teraz czy jest to różniczka zupełna:

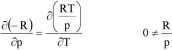
Wniosek: praca mechaniczna nie jest funkcja stanu gazu doskonałego, chociaż jest parametrem stanu.

I. zasada termodynamiki

Pierwsze sformułowanie tej zasady zawdzięczamy Juliuszowi Robertowi Mayerowi (1942). Uzupełnił ja Helmholtz w roku 1947. Mówi ona, że suma wszystkich rodzajów energii w układzie zamkniętym pozostaje stała. Po opublikowaniu teorii Einsteina Henri Poincare sformułował ja w 1908 roku w nieco przekorny sposób: „Istnieje coś, co jest stałe w układzie zamkniętym”.

Ale co to jest to „coś”? Jest ono stałe w układzie zamkniętym, tzn. nie wymieniającym materii z otoczeniem. Jest funkcja stanu, bo jej różniczka w układzie zamkniętym jest równa 0. Nie jest to praca, bo praca nie jest funkcja stanu, ale ma z pracą i energią coś wspólnego. Przyjęto nazywać to „coś” energia wewnętrzną i oznaczać symbolem U.

Współcześnie I zasadę termodynamiki zapisujemy w postaci: dU = dQ + dW,

a więc przyrost energii wewnętrznej jest sumą przyrostu ciepła i pracy wykonanej nad układem. W tej postaci nie można jeszcze wykazać, że różniczka energii wewnętrznej jest różniczką zupełną, ale wykażemy to w toku dalszego wykładu.

I. zasada termodynamiki była badana na gruncie biologii jeszcze przed jej precyzyjnym sformułowaniem. Już w roku 1777 Lavoisier zastanawiał się nad związkiem ilości wydzielanego przez zwierzą ciepła z ciepłem uzyskanym przy spalaniu pożywienia w trakcie oddychania. W kilka lat później Lavoisier i Laplace przeprowadzili pierwsze ilościowe badania kalorymetryczne na świnkach morskich. Potwierdziły one w pełni stosowalność zasady zachowania energii również w