5806256264

Część III: Termodynamika układów biologicznych

W przypadku strumieni sprzężonych niektóre strumienie mogą płynąć „pod prąd” odpowiadających im sił napędowych o ile napędzająje inne strumienie.

Pojawia się teraz problem, jaka jest postać funkcji f(xi,..,x„) w powyższym równaniu. Jak dotychczas przyjmuje się najczęściej, że jest to zależność liniowa:

J, = L,,x, +L₁₂x₂ h-----l-L_lnx_n

J₂ = L₂₁x, +L₂₂x₂ H-----hL_2nx_n

J_n = L_nlx, +L_n2x₂ H-----h L_nn^xn

Taki układ równań można zapisać w zapisie macierzowym w dużo bardziej zwartej formie jako:

J = LX

gdzie: J - kolumnowa macierz strumieni

L - kwadratowa macierz współczynników X - kolumnowa macierz sił napędowych

Ponadto, w 1931 roku Onsager wykazał, że Ly = Lji, czyli że macierz współczynników jest macierzą symetryczną.

Siłę sprzężenia pomiędzy strumieniami opisuje wielkość:

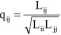
zwana stopniem sprzężenia. Gdy qy = 0, czyli Ly = 0, mamy do czynienia z brakiem sprzężenia strumieni i oraz j. Gdy qy = 1 mamy do czynienia ze sprzężeniem całkowitym.

Przykład 1.

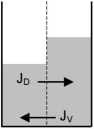
Ci > C₂

Rozważmy układ składający się z dwóch roztworów tej samej substancji o różnych, lecz niedużych stężeniach. Roztwory te znajdują się w dwóch różnych częściach naczynia rozdzielonych błoną (rys. obok). W układzie występują dwie siły napędowe: i) różnica potencjału chemicznego substancji rozpuszczonej wynikająca z różnicy stężeń, oraz ii) różnica ciśnienia hydrostatycznego. Przy niskich stężeniach roztworu potencjał chemiczny rozpuszczalnika jest praktycznie jednakowy w obu częściach układu. Tak więc w układzie pojawić się powinny dwa strumienie: J_D - strumień dyfuzyjny substancji oraz J_v - strumień objętościowy roztworu.

Potencjał chemiczny substancji rozpuszczonej wynosi: p = RT ln c. Różnica potencjału chemicznego, Ap, dana jest więc wzorem:

Ap = RTlnc, -RTlnc₂ = RTln—

^C2

Zakładając występowanie sprzężenia pomiędzy strumieniami otrzymujemy zależności:

J_D =L_DDAp + L_DVAp J_v =L_DVAp + L_wAp

gdzie: L_Dd - współczynnik dyfuzji substancji w błonie

L_w - współczynnik filtracji błony (przepuszczalność hydrauliczna)

14