5806256265

Część III: Termodynamika układów biologicznych

L_dv - współczynnik ultrafiltracji lub osmozy

Z faktu występowania sprzężeń pomiędzy strumieniami wynika istnienie dwóch ciekawych zjawisk: ultrafiltracji - przepływu substancji pod wpływem różnicy ciśnienia hydrostatycznego oraz osmozy -przepływu rozpuszczalnika pod wpływem różnicy stężenia substancji rozpuszczonej.

Przykład 2.

Rozważmy układ otwarty, do którego może wnikać z otoczenia substancję M. Wewnątrz układu substancja ta przekształcana jest z szybkością v w substancję N. Substancja N może dyfundować do otoczenia. Ponadto przez granicę układu może dyfundować substancja O, z która nic się w układzie nie dzieje. Strumienie poszczególnych substancji nie są ze sobą sprzężone i można je opisać zależnościami:

Z dwóch pierwszych równań wynika, że strumień substancji M wpływający do układu równy jest co do wartości strumieniowi substancji N wypływającemu z układu, a oba te strumienie równe są liczbowo szybkości powstawania substancji N. Z ostatniego równania wynika ponadto, że strumień substancji O jest zerowy. Podstawiając wyrażenia na strumienie otrzymujemy:

LMMAfl_M-V = 0

LnnAUn ^{+v =} 0

LooAHo ^— 0

Można teraz wyznaczyć różnice potencjałów chemicznych poszczególnych substancji w stanie stacjonarnym:

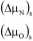
^lmm V

Lnn

= 0

Tak więc różnice potencjałów chemicznych substancji M i N zależą od szybkości przemiany i od współczynników dyfuzji poszczególnych substancji. Potencjał chemiczny substancji O jest identyczny w układzie i w otoczeniu.

Przykład 3.

Rozważmy teraz jak będzie wyglądał stan stacjonarny takiego samego układu, jeżeli pomiędzy strumieniami substancji M i O występuje sprzężenie.

=^LMM^Ał‘M^+L0U^Al*0 ⁼ L_V.,A^_V

Jo=L_OMAłiM+WHio

W stanie stacjonarnym ilość poszczególnych substancji w układzie nie ulega zmianie, co możemy zapisać jako: