122

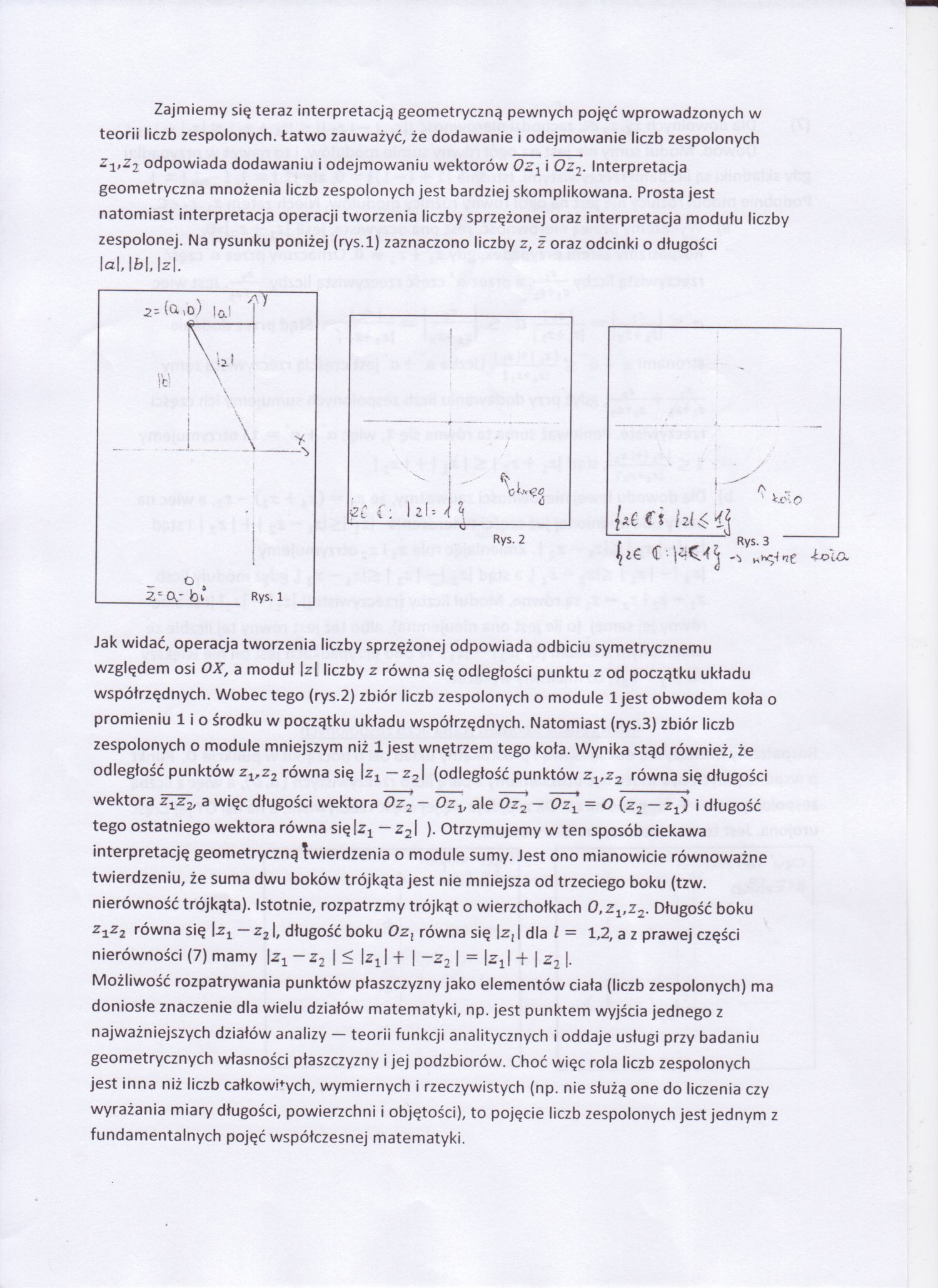
Zajmiemy się teraz interpretacją geometryczną pewnych pojęć wprowadzonych w teorii liczb zespolonych. Łatwo zauważyć, że dodawanie i odejmowanie liczb zespolonych z_ltz₂ odpowiada dodawaniu i odejmowaniu wektorów 0z_x i Oz₂. Interpretacja geometryczna mnożenia liczb zespolonych jest bardziej skomplikowana. Prosta jest natomiast interpretacja operacji tworzenia liczby sprzężonej oraz interpretacja modułu liczby zespolonej. Na rysunku poniżej (rys.l) zaznaczono liczby z, z oraz odcinki o długości \a\, \b\, \z\.

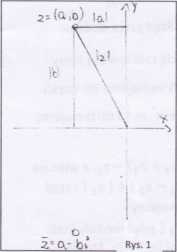
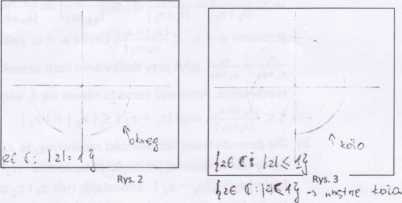
Jak widać, operacja tworzenia liczby sprzężonej odpowiada odbiciu symetrycznemu względem osi OX, a moduł |zl liczby z równa się odległości punktu z od początku układu współrzędnych. Wobec tego (rys.2) zbiór liczb zespolonych o module ljest obwodem koła o promieniu 1 i o środku w początku układu współrzędnych. Natomiast (rys.3) zbiór liczb zespolonych o module mniejszym niż ljest wnętrzem tego koła. Wynika stąd również, że odległość punktów z_lrz₂ równa się \z_x — z₂\ (odległość punktów z_lrz₂ równa się długości wektora z_tz₂, a więc długości wektora Oz₂ — Oz_v ale Oz₂ - Oz_x = O (z₂ — z_Ł) i długość tego ostatniego wektora równa się— z₂\ )■ Otrzymujemy w ten sposób ciekawa interpretację geometryczną twierdzenia o module sumy. Jest ono mianowicie równoważne twierdzeniu, że suma dwu boków trójkąta jest nie mniejsza od trzeciego boku (tzw. nierówność trójkąta). Istotnie, rozpatrzmy trójkąt o wierzchołkach 0,z₁,z₂. Długość boku z_xz₂ równa się \z₁ — z₂1, długość boku Oz, równa się |z,| dla l = 1,2, a z prawej części nierówności (7) mamy \z₁—z₂ | < kj + | ~z₂ | = IzJ + | z₂ I-

Możliwość rozpatrywania punktów płaszczyzny jako elementów ciała (liczb zespolonych) ma doniosłe znaczenie dla wielu działów matematyki, np. jest punktem wyjścia jednego z najważniejszych działów analizy — teorii funkcji analitycznych i oddaje usługi przy badaniu geometrycznych własności płaszczyzny i jej podzbiorów. Choć więc rola liczb zespolonych jest inna niż liczb całkowitych, wymiernych i rzeczywistych (np. nie służą one do liczenia czy wyrażania miary długości, powierzchni i objętości), to pojęcie liczb zespolonych jest jednym z fundamentalnych pojęć współczesnej matematyki.