13cz2

~y.\

Matematyka II. Zbiór zadań

Lisika, {‘h

*2.145. Dl.i jakich wartości parametru m równanie ma dwa różne rzeczywiste pierwiastki dodatnie?

■t

a)    X^J -mx + m(m --1) ■ 0;    c) x² + 3mx + 2m² + 2 = 0;

4

b)    x² - 2mx-m² +4 = 0;    d) x² - 2(m - 2)x + m² - 2m-3 = 0 .

*2.146. Dla jakich wartości parametru m równanie ma dwa różne pierwiastki rzeczywiste jednakowych znaków?

a)    x² + 2(m + 4)x + m² -2m = 0;    c) x² + (m-3 )x +-m(m + 2) = 0;

4

b)    x²-2(m-1)x + m²-5 = 0;    d) 2x² + (m -9)x + m² + 3m + 4 = 0.

*2.147. Dla jakich wartości parametru m równanie ma dwa różne rozwiązania rzeczywiste ujemne?

a) x² + mx-m + 3 = 0;    c) x² -2mx + m² -4 = 0;

b) x² -2(m + 3)x + m² -1 = 0;    d) x² + 5mx + 4m² -3m = 0.

■    ¹2.148. Dla jakich wartości parametru m suma kwadratów pierwiastków równania jest

równa 5:

i a) x² + 5mx + 2Om -8=0; 5 = 400; c) x² -mx - m(m + 1) = 0; 5 = 1;

.

b) x² + 2 (m -1)x + m² - 4 = 0; S = 12; d) x² -3 mx + m- 4 = 0; S = 8.

*2.149. Dla jakich wartości parametru m suma kwadratów pierwiastków równania:

a)    x² + (m - 2)x - m -1 = 0 jest najmniejsza?

b)    x² -(m + l)x + m = 0 jest najmniejsza?    ₉

c)    x² -mx + m² -3m - 2 = 0 jest największa?

d)    x² + 2mx + 2m² -3m = 0 jest największa?

*2.150. Dla jakich wartości parametru m:

a)    odwrotność sumy pierwiastków równania 2x + m(1 -x²) = 2+ 2x² jest dodatnia?

b)    suma pierwiastków równania x² -2m(x -1) -1 = Ojest równa sumie kwadratów tych pierwiastków?

c)    suma odwrotności pierwiastków równania x² + mx -16 = 0 jest równa - 4?

d)    równanie x² +mx + 2m-2 = 0 ma dwa pierwiastki, z których jeden jest sinusem, a drugi cosinusem tego samego kąta?

e)    jeden pierwiastek równania x² -(m + 1)x + 1,2m = Ojest równy sinusowi, a drugi cosi-nusowi tego samego kąta ostrego?

• zapisujemy warunki, jakie powinien spełniać trójmian kwadratowy, aby miał dwa różne miejsca zerowe mniejsze od 2:

A > 0 - aby istniały dwa różne miejsca zerowe,

f(2) > Ol ...    ui • • a-i

*w <²

z których powstaje układ nierówności:

m² - 4m > 0

4+ 2 m + m > 0

m „

--< 2

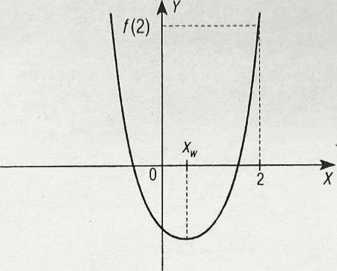
- aby miejsca zerowe były mniejsze od 2,

• rozwiązujemy otrzymany układ nierówności: m e (-oo, O) co (4, + co)

. m > -1-    , skąd m e^-1^, oju(4,+<x>)

m > -4

Równanie ma dwa różne pierwiastki mniejsze od 2 dla parametru m e (-1,0) u (4, +oo). Postępując podobnie, wyznacz te wartości parametru m, dla których:

a)    każdy z dwóch różnych pierwiastków równania x² -6mx.+ 2-2m + 9m² =0 jest większy od 3;

b)    każdy z dwóch różnych pierwiastków równania x² + mx + 4 = Ojest mniejszy od 4;

c)    pierwiastki Xi, x₂ równania 2x² -2(2m + 1)x + m(m -1) = Ospełniają warunek x, < m < x₂;

d)    oba pierwiastki równania x² -mx + 2 = 0 należą do przedziału (0, 3). ²

1

2.151. Aby odpowiedzieć na pytanie: „Dla jakich wartości parametru m, równanie X² + mx + m = 0 ma dwa różne pierwiastki mniejsze od 2?", możemy postąpić tak:

• szkicujemy wykres funkcji kwadratowej f(x) = X² + mx + m odpowiadający warunkom zadania;    $

2

2.152. Dla jakich wartości parametru m :

a)    nierówność (x -3m)(x -m - 3) < 0 jest spełniona przez każdą liczbę rzeczywistą należącą do przedziału (1, 3) ?

b)    nierówność (x - 2m — 1 )(x-m) < 0 jest spełniona przez każdą liczbę rzeczywistą należącą do przedziału (1, 2) ?