146 147

146 Zadanie transportowe i problem komiwojażera

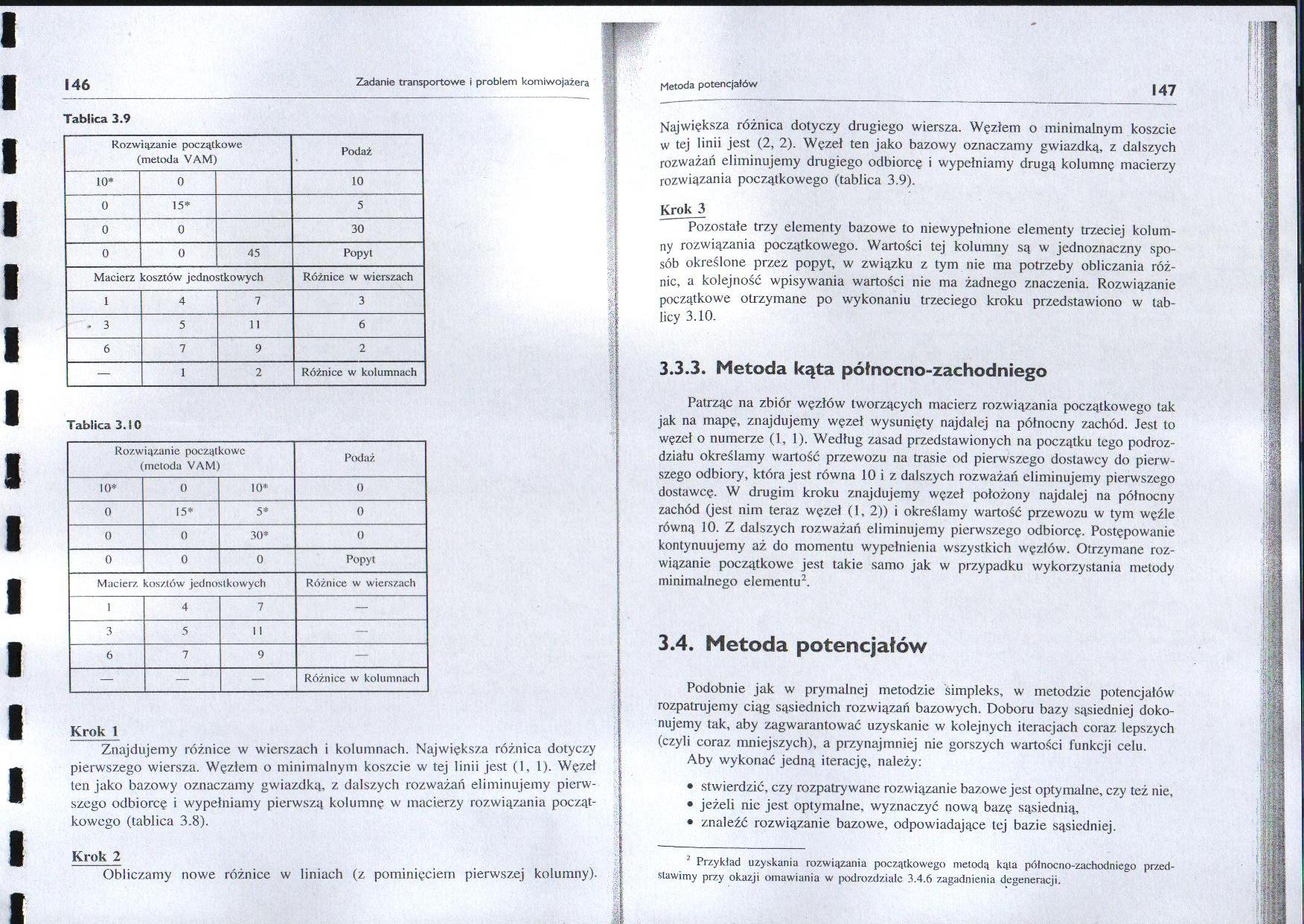
Tablica 3.9

Rozwiązanie początkowe (metoda VAM)			Podaż
10*	0		10
0	15*		5
0	0		30
0	0	45	Popyt
Macierz kosztów jednostkowych			Różnice w wierszach
I	4	7	3
. 3	5	11	6
6	7	9	2
—	1	2	Różnice w kolumnach

Tablica 3.10

Rozwiązanie początkowe (metoda VAM)			Podaż
10*	0	10*	0
0	15*	5*	0
0	0	30*	0
0	0	0	Popyt
Macierz kosztów jednostkowych			Różnice w wierszach
i	4	7	—
3	5	11
6	7	9	—
—	—		Różnice w kolumnach

Krok 1

Znajdujemy różnice w wierszach i kolumnach. Największa różnica dotyczy pierwszego wiersza. Węzłem o minimalnym koszcie w tej linii jest (1, 1). Węzeł len jako bazowy oznaczamy gwiazdka, z dalszych rozważań eliminujemy pierwszego odbiorcę i wypełniamy pierwsza kolumnę w macierzy rozwiązania początkowego (tablica 3.8).

Krok 2

Obliczamy nowe różnice w liniach (z pominięciem pierwszej kolumny).

Największa różnica dotyczy drugiego wiersza. Węzłem o minimalnym koszcie w tej linii jest (2, 2). Węzeł ten jako bazowy oznaczamy gwiazdką, z dalszych rozważań eliminujemy drugiego odbiorcę i wypełniamy drugą kolumnę macierzy rozwiązania początkowego (tablica 3.9).

Krok 3

Pozostałe trzy elementy bazowe to niewypełnione elementy trzeciej kolumny rozwiązania początkowego. Wartości tej kolumny są w jednoznaczny sposób określone przez popyt, w związku z tym nie ma potrzeby obliczania różnic, a kolejność wpisywania wartości nic ma żadnego znaczenia. Rozwiązanie początkowe otrzymane po wykonaniu trzeciego kroku przedstawiono w tablicy 3.10.

3.3.3. Metoda kąta północno-zachodniego

Patrząc na zbiór węzłów tworzących macierz rozwiązania początkowego tak jak na mapę, znajdujemy węzeł wysunięty najdalej na północny zachód. Jest to węzeł o numerze (1, 1). Według zasad przedstawionych na początku tego podrozdziału określamy wartość przewozu na trasie od pierwszego dostawcy do pierwszego odbiory, która jest równa 10 i z dalszych rozważań eliminujemy pierwszego dostawcę. W drugim kroku znajdujemy węzeł położony najdalej na północny zachód (jest nim teraz węzeł (1.2)) i określamy wartość przewozu w tym węźle równą 10. Z dalszych rozważań eliminujemy pierwszego odbiorcę. Postępowanie kontynuujemy aż do momentu wypełnienia wszystkich węzłów. Otrzymane rozwiązanie początkowe jest takie samo jak w przypadku wykorzystania metody minimalnego elementu¹.

3.4. Metoda potencjałów

Podobnie jak w prymalnej metodzie simpleks, w metodzie potencjałów rozpatrujemy ciąg sąsiednich rozwiązań bazowych. Doboru bazy sąsiedniej dokonujemy tak, aby zagwarantować uzyskanie w kolejnych iteracjach coraz lepszych (czyli coraz mniejszych), a przynajmniej nie gorszych wartości funkcji celu.

Aby wykonać jedną iterację, należy:

• stwierdzić, czy rozpatrywane rozwiązanie bazowe jest optymalne, czy też nie,

• jeżeli nie jest optymalne, wyznaczyć nową bazę sąsiednią,

• znaleźć rozwiązanie bazowe, odpowiadające tej bazie sąsiedniej.

Przykład uzyskania rozwiązania początkowego metodą kąta północno-zachodniego przedstawimy przy okazji omawiania w podrozdziale 3.4.6 zagadnienia degeneracji.