178 179

178 Zadanie transportowe i problem komiwojażera

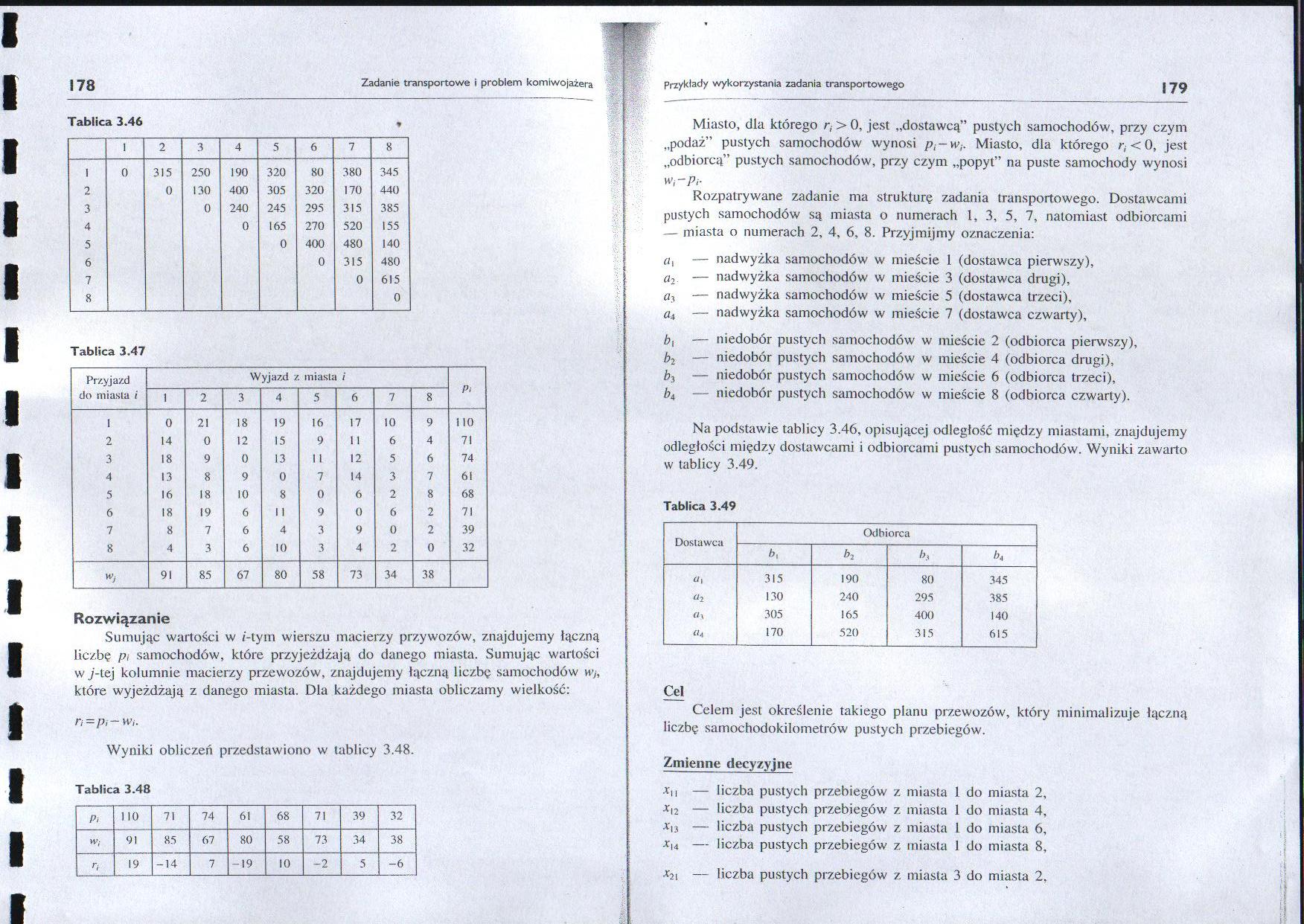
Tablica 3.46

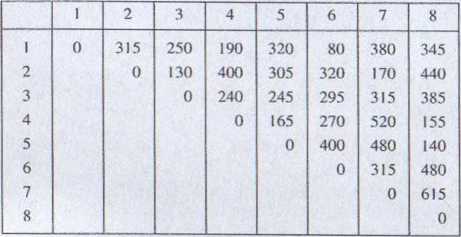
Tablica 3.47

Przyjazd do mi as la i			Wyjazd z		miasla /				Pi
	1	2	3	4	5	6	7	8
i	0	21	18	19	16	17	10	9	110
2	14	0	12	15	9	11	6	4	71
3	18	9	0	13	1 1	12	5	6	74
4	13	8	9	0	7	14	3	7	61
5	16	18	10	8	0	6	2	8	68
6	18	19	6	11	9	0	6	2	71
7	8	7	6	4	3	9	0	2	39
8	4	3	6	10	3	4	2	0	32
^wi	91	85	67	80	58	73	34	38

Rozwiązanie

Sumując wartości w /'-tym wierszu macierzy przywozów, znajdujemy łączną liczbę pi samochodów, które przyjeżdżają do danego miasta. Sumując wartości wj-tej kolumnie macierzy przewozów, znajdujemy łączną liczbę samochodów w„ które wyjeżdżają z danego miasta. Dla każdego miasta obliczamy wielkość:

n=p,~Wi.

Wyniki obliczeń przedstawiono w tablicy 3.48.

Tablica 3.48

Pi	110	71	74	61	68	71	39	32
W;	91	85	67	80	58	73	34	38
r}	19	-14	7	-19	10	-2	5	-6

Miasto, dla którego r, > 0, jest „dostawcą” pustych samochodów, przy czym „podaż” pustych samochodów wynosi p.-w-,. Miasto, dla którego r,<0, jest „odbiorcą” pustych samochodów, przy czym „popyt” na puste samochody wynosi

Wi-Pi-

Rozpatrywane zadanie ma strukturę zadania transportowego. Dostawcami pustych samochodów są miasta o numerach 1, 3, 5, 7, natomiast odbiorcami — miasta o numerach 2, 4, 6, 8. Przyjmijmy oznaczenia:

<7,    —    nadwyżka    samochodów    w    mieście    1    (dostawca    pierwszy),

«₂    —    nadwyżka    samochodów    w    mieście    3    (dostawca    drugi),

0i    —    nadwyżka    samochodów    w    mieście    5    (dostawca    trzeci),

a_t    —    nadwyżka    samochodów    w    mieście    7    (dostawca    czwarty),

/b,    —    niedobór    pustych    samochodów    w    mieście    2    (odbiorca    pierwszy),

b₂    —    niedobór    pustych    samochodów    w    mieście    4    (odbiorca    drugi),

b₃    —    niedobór    pustych    samochodów    w    mieście    6    (odbiorca    trzeci),

b_t    —    niedobór    pustych    samochodów    w    mieście    8    (odbiorca    czwarty).

Na podstawie tablicy 3.46, opisującej odległość między miastami, znajdujemy odległości między dostawcami i odbiorcami pustych samochodów. Wyniki zawarto w tablicy 3.49.

Tablica 3.49

Dostawca	Odbiorca
	b,	b2	by	bt
Ot	315	190	80	345
“2	130	240	295	385
U\	305	165	400	140
‘U	170	520	315	615

Cel

Celem jest określenie takiego planu przewozów, który minimalizuje łączną liczbę samochodokilometrów pustych przebiegów.

Zmienne decyzyjne

*ii    —    liczba    pustych    przebiegów    z    miasta    1    do    miasta    2,

*12    —    liczba    pustych    przebiegów    z    miasta    1    do    miasta    4,

*b    —    liczba    pustych    przebiegów    z    miasta    1    do    miasta    6,

*m    —    liczba    pustych    przebiegów    z    miasta    1    do    miasta    8,

*2i    —    liczba    pustych    przebiegów    z    miasta    3    do    miasta    2,