144 145

144 Zadanie transportowe i problem komiwojażera

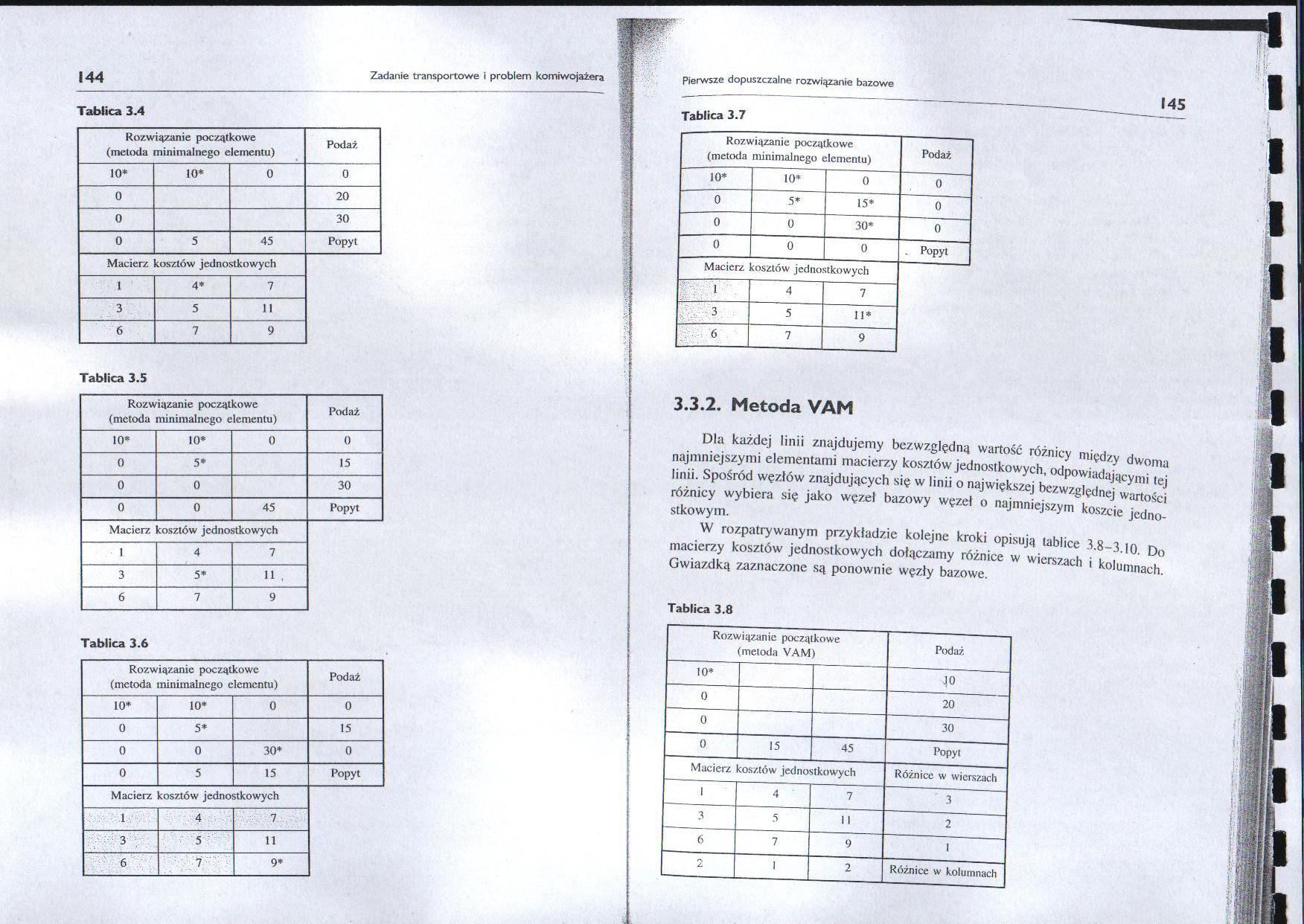
Tablica 3.4

Rozwiązanie początkowe (metoda minimalnego elementu)			Podaż
10*	10*	0	0
0			20
0			30
0	5	45	Popyt
Macierz kosztów jednostkowych
i	4*	7
3	5	11
6	7	9

Tablica 3.5

Rozwiązanie początkowe (metoda minimalnego elementu)			Podaż
10*	10*	0	0
0	5*		15
0	0		30
0	0	45	Popyt
Macierz kosztów jednostkowych
1	4	7
3	5*	U •
6	7	9

Tablica 3.6

Rozwiązanie początkowe (metoda minimalnego elementu)			Podaż
10*	10*	0	0
0	5*		15
0	0	30*	0
0	5	15	Popyt
Macierz kosztów jednostkowych
1	4	7
3	5	11
6	7	9*

pierwsze dopuszczalne rozwiązanie bazowe

Tablica 3.7

Rozwiązanie początkowe (metoda minimalnego elementu)			Podaż
10*	10*	0	0
0	5*	15*	0
0	0	30*	0
0	0	0	Popyt
Macierz kosztów jednostkowych
1	4	7
^3	5	11*
6	7	9

3.3.2. Metoda VAM

Dla każdej linii znajdujemy bezwzględna wartość różnicy między dwoma najmniejszymi elementami macierzy kosztów jednostkowych, odpowiadającymi tej linii. Spośród węzłów znajdujących się w linii o największej bezwzględnej wartości różnicy wybiera się jako węzeł bazowy węzeł o najmniejszym koszcie jednostkowym.

W rozpatrywanym przykładzie kolejne kroki opisują tablice 3.8-3.10. Do macierzy kosztów jednostkowych dołączamy różnice w wierszach i kolumnach. Gwiazdką zaznaczone są ponownie węzły bazowe.

Tablica 3.8

Rozwiązanie początkowe (metoda VAM)			Podaż
10*			JO
0			20
0			30
0	15	45	Popyt
Macierz kosztów jednostkowych			Różnice w wierszach
1	4	7	3
3	5	11	2
6	7	9	1
2	1	2	Różnice w kolumnach