138 139

138 Zadanie transportowe i problem komiwojażera

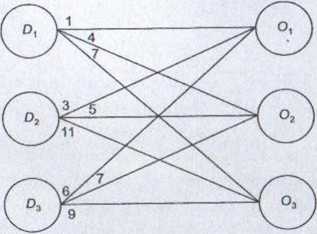
Rysunek 3.1

20

20

30

10

45

Podaż

Popyt

Przystąpimy do budowy modelu matematycznego. Celem jest minimalizacja kosztów transportu między wszystkimi dostawcami i odbiorcami. Oznaczając przez x,j wielkość przewozu od /-tego dostawcy do y-tego odbiorcy, możemy obliczyć łączny koszt transportu oraz warunki ograniczające, po jednym dla każdego dostawcy i każdego odbiorcy. Nie zapominamy przy tym o warunkach nieujemności dla wszystkich zmiennych decyzyjnych. Otrzymujemy następujące zadanie:

f(xu, x_n, x_tu x₂„ X22, x_2}, X_U, x_t2, *33) = x,, + 4.v,₂ + 7.*,3 + 3x_2i + 5x₂₂ + I 1*13 +

+ 6*, 1 + 7x₃₂ + 9xu    min,

(3.1)

(3.2)

(3.3)

(3.4)

(3.5)

(3.6)

:

!

i

I

x_u +x_l2 + x_n = 20, x₂i +x₂₂ + x₂) = 20,

Jf.n +Xj2+JC.m = 30,

X\ 1 +x_3l + a'₃i = 10,

X[₂ x₂₂ + x₂₂ — 15, X\3 +    + JC33 — 45,

X| I, ...,    0.

Warunki ograniczające odczytujemy następująco:

Warunek (3.1):

~~ Ilość towaru wysłanego przez dostawcę D, odbiorcom O,, O, i O, jest równa podaży tego dostawcy i wynosi 20.

Warunek (3.2):

Ilość towaru wysłanego przez dostawcę D₂ odbiorcom 0\, 0₂ i 0₃ jest równa podaży tego dostawcy i wynosi 20.

Warunek (3.3):

Ilość towaru wysianego przez dostawcę Zż_, odbiorcom (?,. 0₂ i 0₃ jest równa podaży tego dostawcy i wynosi 30.

Warunek (3.4):

Ilość towaru otrzymanego przez odbiorcę O_t od dostawców /),, f)₂ i Dj jest równa popytowi tego odbiorcy i wynosi 10.

Warunek (3.5):

Ilość towaru otrzymanego przez odbiorcę 0₂ od dostawców D_h D₂ i D_, jest równa popytowi tego odbiorcy i wynosi 15.

Warunek (3.6):

Ilość towaru otrzymanego przez odbiorcę O_s od dostawców D_t, D₂ i /), jest równa popytowi tego odbiorcy i wynosi 45.

Do rozwiązania tego zadania możemy wykorzystać prymalną metodę simpleks i program SIMP.EXE. Otrzymujemy:

*ii = 5, x,₂= 0, *_l?= 15,

*₂₎ = 5, x₂₂- 15, x₂₃ = 0,

*31 =0. *32= 0, *33=30.

Minimalny koszt transportu wynosi 470.

Jeżeli spróbujemy to niewielkie zadanie transportowe rozwiązać za pomocą metody simpleks, to zobaczymy, że powstanie zadanie programowania liniowego o dużych rozmiarach. Mamy 9 zmiennych decyzyjnych, ponadto — ze względu na to, że warunki ograniczające są w postaci równości — trzeba dodatkowo wprowadzić 6 zmiennych sztucznych. Stosując metodę simpleks, musimy przeprowadzić 13 iteracji. Przytoczone powyżej okoliczności wskazują na to, że rozwiązanie zadania transportowego prymalną metodą simpleks jest uciążliwe. Z lego też względu przedstawimy dalej modyfikację metody simpleks, wykorzystując związki między zadaniem prymalnym i dualnym. Pozwolą one na uproszczenie sposobu rozwiązania zadania.

3.2.2. Zadanie dualne

do zadania transportowego

Zapiszemy zadanie dualne do rozpatrywanego przez nas zadania transportowego. Wygodnie jest rozpatrywać zadanie transportowe jako problem prymalny z kryterium maksymalizacji, dlatego też mnożymy współczynniki funkcji celu przez - 1 i otrzymujemy funkcję celu w zadaniu prymalnym w postaci:

x4*|2 — 7*|3 3*₂| 5*22 11*23 — 6*3| — 7*3₂ — 9*33 —^ mux.

Zmienne w zadaniu dualnym, odpowiadające ograniczeniom dla kolejnych dostawców, oznaczymy jako n,, u₂ i u₃, natomiast zmienne w zadaniu dualnym, odpowiadające ograniczeniom dla kolejnych odbiorców, jako v,, v₂ i V3. Stosujemy