158 159

158 Zadanie transportowe i problem komiwojażera

Iteracja 1

Tworzymy układ równań liniowych odpowiadający rozpatrywanej bazie:

u, + v, +7 = 0, w, + Vj + 4 = 0, u₂ + v₂ +6 = 0,

U 2 + ^3 + i — 0,

u_}+v₂ + 5 = 0.

Dla m,=0 otrzymujemy rozwiązanie:

m i = 0, v,=-7,

u₂ = -2, v₂ = —4.

Mj = - 6, V'3 = I.

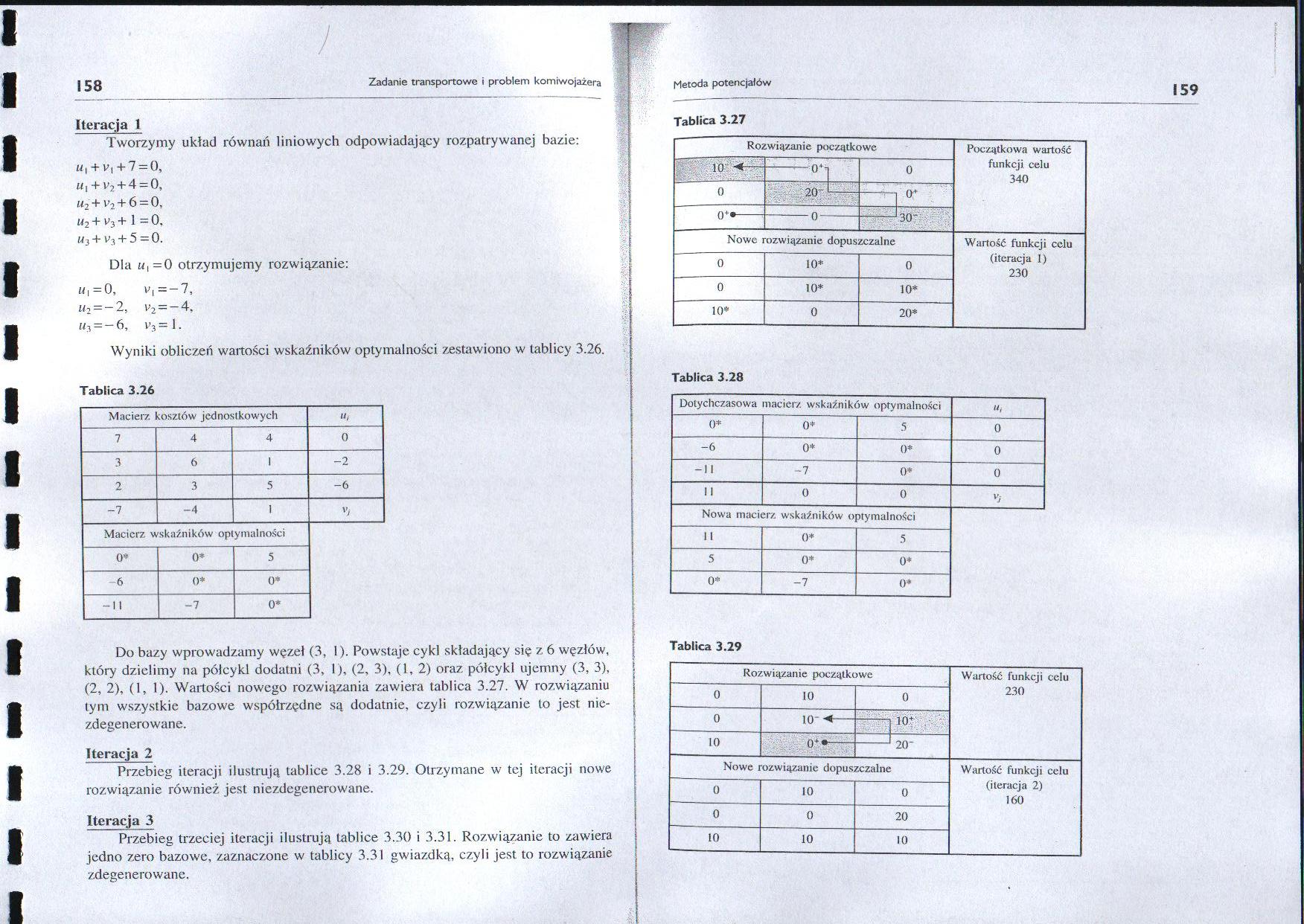
Wyniki obliczeń wartości wskaźników optymalności zestawiono w tablicy 3.26.

Tablica 3.26

Macierz kosztów jednostkowych			U_f
7	4	4	0
3	6	1	-2
2	3	5	-6
-7	-4	1	^VJ
Macierz wskaźników optymalności
0*	0*	5
6	0*	0*
-II	-7	0*

Do bazy wprowadzamy węzeł (3, 1). Powstaje cykl składający się z 6 węzłów, który dzielimy na pólcykl dodatni (3, 1), (2, 3), (1, 2) oraz półcykl ujemny (3, 3), (2, 2), (1, 1). Wartości nowego rozwiązania zawiera tablica 3.27. W rozwiązaniu tym wszystkie bazowe współrzędne są dodatnie, czyli rozwiązanie to jest nie-zdegenerowane.

Iteracja 2

Przebieg iteracji ilustrują tablice 3.28 i 3.29. Otrzymane w tej iteracji nowe rozwiązanie również jest niezdegenerowane.

Iteracja 3

Przebieg trzeciej iteracji ilustrują tablice 3.30 i 3.31. Rozwiązanie to zawiera jedno zero bazowe, zaznaczone w tablicy 3.31 gwiazdką, czyli jest to rozwiązanie /.degenerowane.

Tablica 3.27

Rozwiązanie początkowe				Początkowa wartość funkcji celu 340
10 <—	--'—O⁴'	0
0	• Ań- .		0*
	zU
			30-
	U
Nowe rozwiązanie dopuszczalne				Wartość funkcji celu (iteracja 1) 230
0	10*	0
0	10*	10*
10*	0	20*

Tablica 3.28

Dotychczasowa macierz wskaźników optymalności			Uj
0*	0*	5	0
-6	0*	0*	0
-II	-7	0*	0
II	0	0	^vi
Nowa macierz wskaźników optymalności
11	0*	5
5	0*	0*
0*	-7	0*

Tablica 3.29

Rozwiązanie początkowe				Wartość funkcji celu 230
0	10	0
0	io- <—		10*
10	o⁴»-		20-
Nowe rozwiązanie dopuszczalne				Wartość funkcji celu (iteracja 2) 160
0	10	0
0	0	20
10	10	10