156 157

156 Zadanie transportowe i problem komiwojażera

X| i = 10

oraz

= 10-10=0,

b\ = 10- 10 = 0.

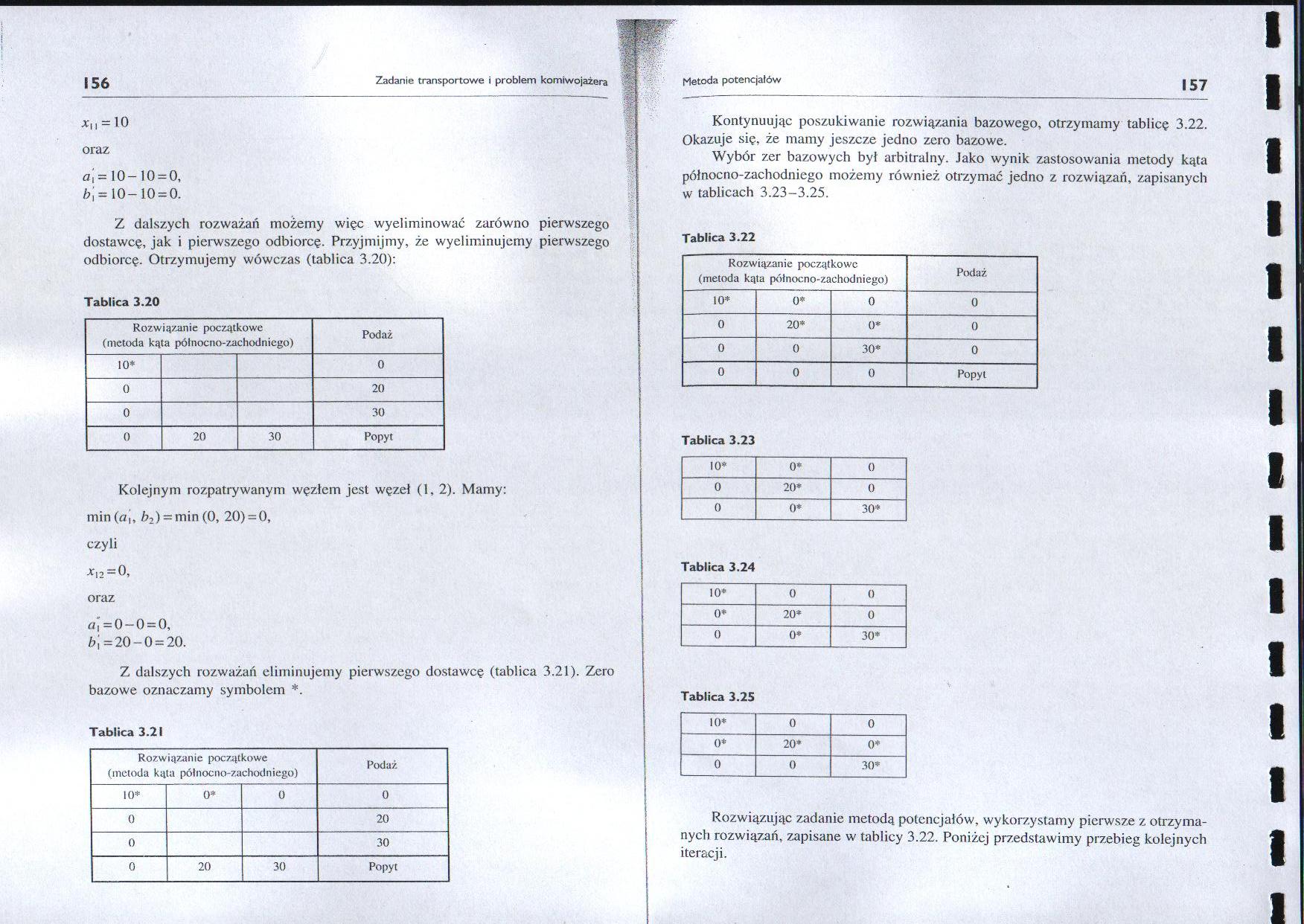
Z dalszych rozważań możemy więc wyeliminować zarówno pierwszego dostawcę, jak i pierwszego odbiorcę. Przyjmijmy, że wyeliminujemy pierwszego odbiorcę. Otrzymujemy wówczas (tablica 3.20):

Tablica 3.20

Rozwiązanie początkowe (metoda kąta północno-zachodniego)			Podaż
10*			0
0			20
0			30
0	20	30	Popyt

Kolejnym rozpatrywanym węzłem jest węzeł (1, 2). Mamy: min (aj, b₂) = min(0, 20) =0, czyli X\2 =0, oraz

«;=o-o=o,

b\ =20-0 = 20.

Z dalszych rozważań eliminujemy pierwszego dostawcę (tablica 3.21). Zero bazowe oznaczamy symbolem *.

Tablica 3.21

Rozwiązanie początkowe (metoda kąta północno-zachodniego)			Podaż
10*	0*	0	0
0			20
0			30
0	20	30	Popyt

Kontynuując poszukiwanie rozwiązania bazowego, otrzymamy tablicę 3.22. Okazuje się, że mamy jeszcze jedno zero bazowe.

Wybór zer bazowych był arbitralny. Jako wynik zastosowania metody kąta północno-zachodniego możemy również otrzymać jedno z rozwiązań, zapisanych w tablicach 3.23-3.25.

Tablica 3.22

Rozwiązanie początkowe (metoda kąta północno-zachodniego)			Podaż
10*	0*	0	0
0	20*	0*	0
0	0	30*	0
0	0	0	Popyt

Tablica 3.23
10*	0*	0
0	20*	0
0	0*	30*
Tablica 3.24
10*	0	0
0*	20*	0
0	0*	30*

Tablica 3.25

10*	0	0
0*	20*	0*
0	0	30*

Rozwiązując zadanie metodą potencjałów, wykorzystamy pierwsze z otrzymanych rozwiązań, zapisane w tablicy 3.22. Poniżej przedstawimy przebieg kolejnych iteracji.