166 167

166

Zadanie transportowe i problem komiwojażera

Tablica 3.36

Miasto	i	2	3	4	5
i	—	1	0	0	0
2	0	—	1	0	0
3	0	0	—	1	0
4	0	0	0	—	1
5	1	0	0	0	—

w każdym rozwiązaniu dopuszczalnym zmienne Jt„ są równe 0 dla i - 1, 5,

dlatego leż w tablicy 3.36, przedstawiającej to rozwiązanie węzły o tych numerach zostały usunięte z rozważań.

Wybrane rozwiązanie charakteryzuje się tą własnością, że w każdym wierszu jest dokładnie jedna jedynka, co wynika stąd, że komiwojażer wyjeżdża z każdego z miast dokładnie jeden raz. Również w każdej kolumnie jest dokładnie jedna jedynka, a to dlatego, że wjeżdża on do każdego z miast również dokładnie jeden raz. Tak więc suma elementów każdego wiersza, podobnie jak i suma elementów każdej kolumny, jest równa 1. Zauważmy, że omówione powyżej własności dotyczą dowolnego rozwiązania dopuszczalnego.

Rozpatrywane zadanie zapiszemy jako problem transportowy o 5 dostawcach i 5 odbiorcach, przy czym odpowiednio podaż i popyt dla każdego z nich wynosi 1. Przewóz z miasta i do j (czyli wartość zmiennej x_u) jest równy I, jeżeli planując trasę przejazdu komiwojażera chcemy włączyć ten odcinek do jego marszruty. Aby uniknąć planowania tras zawierających węzły (/, /'), w macierzy odległości D (traktowanej teraz jako macierz kosztów) w każdym węźle (i, i) wpisujemy odpowiednio dużą liczbę (w rozpatrywanym przez nas przypadku wpiszemy wartość r/„ = 100). Otrzymane zadanie przedstawiamy w tablicy 3.37.

Tablica 3.37

Miasto	1	2	3	4	5	Podaż
1	100	10	12	15	11	1
2	10	100	19	10	1 1	1
3	12	19	100	10	12	1
4	15	10	10	100	20	1
5	11	11	12	20	100	1
	1	1	1	1	t	Popyt

Wykorzystując algorytm transportowy, otrzymujemy: x_l2 = 1, x_u = 1, x₃₄= 1, x.,, = 1, x_5l = 1: pozostałe zmienne są równe 0. a optymalna wartość funkcji celu wynosi 52.

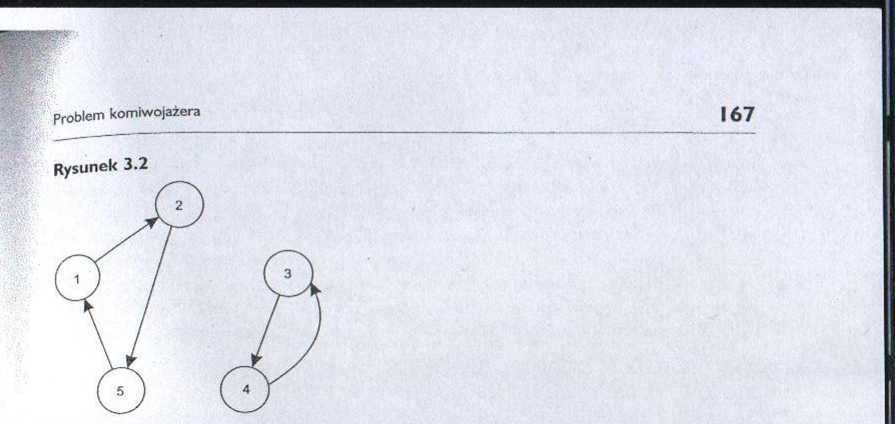
Rozwiązanie to można zilustrować graficznie. W grafie, przedstawionym na rysunku 3.2 wierzchołkami są rozpatrywane miasta, a lukami — zaplanowane odcinki przejazdu komiwojażera.

Stawiany rozwiązaniu wymóg, by rozpocząć podróż w mieście 1 oraz zakończyć ją również w mieście 1 wraz z wymogiem jednokrotnego odwiedzenia pozostałych miast powoduje, że w każdym rozwiązaniu dopuszczalnym znajduje się dokładnie jeden cykl. Otrzymane za pomocą algorytmu transportowego rozwiązanie nie spełnia tego wymogu, gdyż zawiera dwa cykle: pierwszy, obejmujący miasta 1, 2 i 3, oraz dragi, obejmujący miasta 4 i 5. Komiwojażer po odwiedzeniu miasta 3 zbyt prędko wraca do miasta wyjściowego, przez co traci możliwość odwiedzenia miast 4 i 5.

Powyższy przykład wskazuje na to, że zastosowanie, algorytmu transportowego do rozwiązania problemu komiwojażera nic jest poprawne, gdyż w otrzymanym tym sposobem rozwiązaniu może znajdować się więcej niż jeden cykl. Otrzymaną za pomocą algorytmu transportowego długość trasy komiwojażera można więc traktować jedynie jako dolne przybliżenie optymalnej długości trasy⁴.

3.6.2. Zadanie komiwojażera jako zadanie programowania całkowitoliczbowego

Zachowanie ciągłości trasy wymaga wykluczenia wszystkich rozwiązań, w których występują cykle. Cykle jednoelementowe, którym odpowiadają wartości x_u = I eliminujemy w taki sposób, że dla / =1, ..., 5 przyjmujemy x_h - 0 i zmienne te wyłączamy z dalszych rozważań. Wyeliminowanie cyklów jednoelementowych pozwala na to, by pominąć w dalszych rozważaniach cykle czteroelementowe (ponieważ z każdym takim cyklem należałoby związać cykl jednoelementowy, a te

^J Podobnie można traktować długość krawędzi minimalnego drzewa rozpinającego, które zostanie omówione w rozdziale 8.2.