172 173

172 Zadanie transportowe i problem komiwojażera

Tablica 3.39

Chromosom	*12	*13	*14	*15	*21	*23	*24	*25	*31	*32	*34	*35	*41	*42	*44	*4.4	*51	*52	*53	*54
c„	0	i	0	0	0	1	0	1	0	1	0	1	1	0	1	0	0	1	0	0
C\2	1	0	0	0	0	1	0	0	0	0	1	0	0	0	0	0	1	0	0	0
c„	0	0	1	0	1	0	0	0	1	0	0	0	0	0	0	1	0	0	1	0
C M	0	0	0	1	0	0	1	0	0	0	0	0	0	1	0	0	0	0	0	1
	0	0	0	1	0	1	0	0	1	0	0	1	0	0	0	0	1	0	0	1
£|ń	0	0	0	0	0	I	0	0	0	0	0	0	0	1	0	0	0	0	0	1

Rysunek 3.3

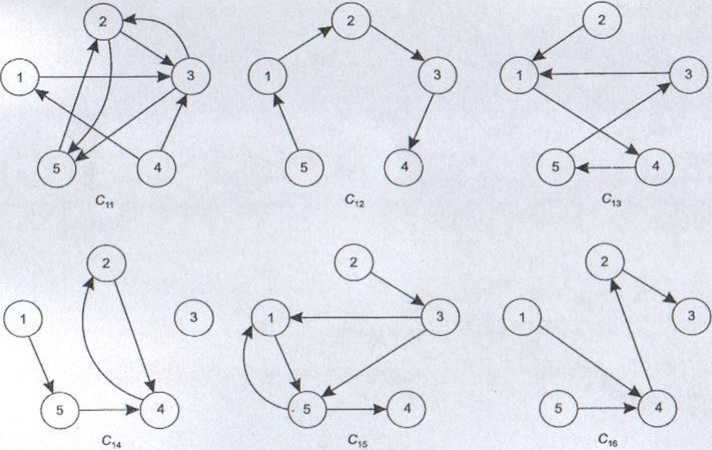
Wartości funkcji przystosowania

Funkcje przystosowania zdefiniujemy jako sumę długości tras wchodzących w skład danego chromosomu, powiększoną o karę za naruszenie ograniczeń. Przyjmiemy, że kara za naruszenie każdego z ograniczeń dla rozwiązań niedopuszczalnych wynosi 100. Obliczymy długości odcinków włączonych do rozpatrywanego rozwiązania, następnie zaś obliczymy, ilokrotnie zostały naruszone ograniczenia w kolejnych wylosowanych chromosomach.

Dla chromosomu C_n długość odcinków, włączonych do rozpatrywanego rozwiązania wynosi 12+19+11 + 19+12+15 + 10+11 = 109. Ograniczenia dotyczące wyjazdu naruszone są dla miast 2, 3 i 4. Natomiast ograniczenia związane z wjazdem naruszone są dla miast 2, 3, 4 i 5. Dwuelementowe cykle występują między miastami 2 i 3 oraz 2 i 5. Tak więc naruszone są ograniczenia o numerach (3.1-3), (3.14) i (3.15), następnie (3.18), (3.19), (3.20) oraz (3.21), a także (3.26) i (3.28). Ponadto można stwierdzić, że ograniczenie o numerze (3.19) jest naruszone dwukrotnie, gdyż w zaplanowanej trasie przewidziano trzy wjazdy do tego miasta. Zatem łączna liczba naruszonych ograniczeń wynosi 9, a uwzględniając dwukrotne naruszenie ograniczenia o numerze (3.19) możemy wyznaczyć karę za dziesięciokrotne naruszenie ograniczeń, wynoszącą 1000 jednostek. Suma długości odcinków włączonych do rozpatrywanego rozwiązania i kar za naruszenie ograniczeń jest więc równa 1109.

W podobny sposób obliczamy długości kolejnych rozwiązań oraz kary za naruszenie ograniczeń. Wyniki tych obliczeń zestawione zostały w tablicy 3.40.

Tablica 3.40

Chromo som	Numery naruszonych ograniczeń	Długość odcin ków	Kara	Wartość funkcji przysto sowania
	(3.13), (3.14), (3.15), (3.18), (3.19). (3.20), (3.21), (3.26), (3.28)	109	1 (XX)	1 109
	(3.15), (3.21)	50	200	250
	(3.17), (3.18)	69	200	269
C»	(3.14), (3.17). (3.19), (3.20), (3.27)	51	500	551
	(3.14), (3.15), (3.16), (3.17), (3.18), (3.19), (3.25)	85	700	785
C,„	(3.14), (3.17), (3.20), (3.21)	64	400	464
Suma				3 428

Średnia wartość funkcji przystosowania dla populacji początkowej wynosi 3428:6 = 571,33, natomiast najlepsza wartość funkcji przystosowania w tej populacji wynosi 250 i osiągnięta jest ona dla chromosomu C,₂.

Prawdopodobieństwo selekcji

W rozpatrywanym przez nas zadaniu minimalizacji prawdopodobieństwo selekcji dla każdego chromosomu z rozpatrywanej populacji obliczymy jako iloraz odwrotności wartości funkcji przystosowania dla lego chromosomu do sumy odwrotności wartości wszystkich funkcji przystosowania dla wszystkich chromosomów z tej populacji. Kolejno wykonane obliczenia przedstawione zostały w tablicy 3.41.

Selekcja i krzyżowanie

Uruchamiamy mechanizm losowy, działający tak, by prawdopodobieństwa wylosowania chromosomów w populacji były takie, jak obliczone w tablicy 3.41