160 161

160 Zadanie transportowe i problem komiwojażera

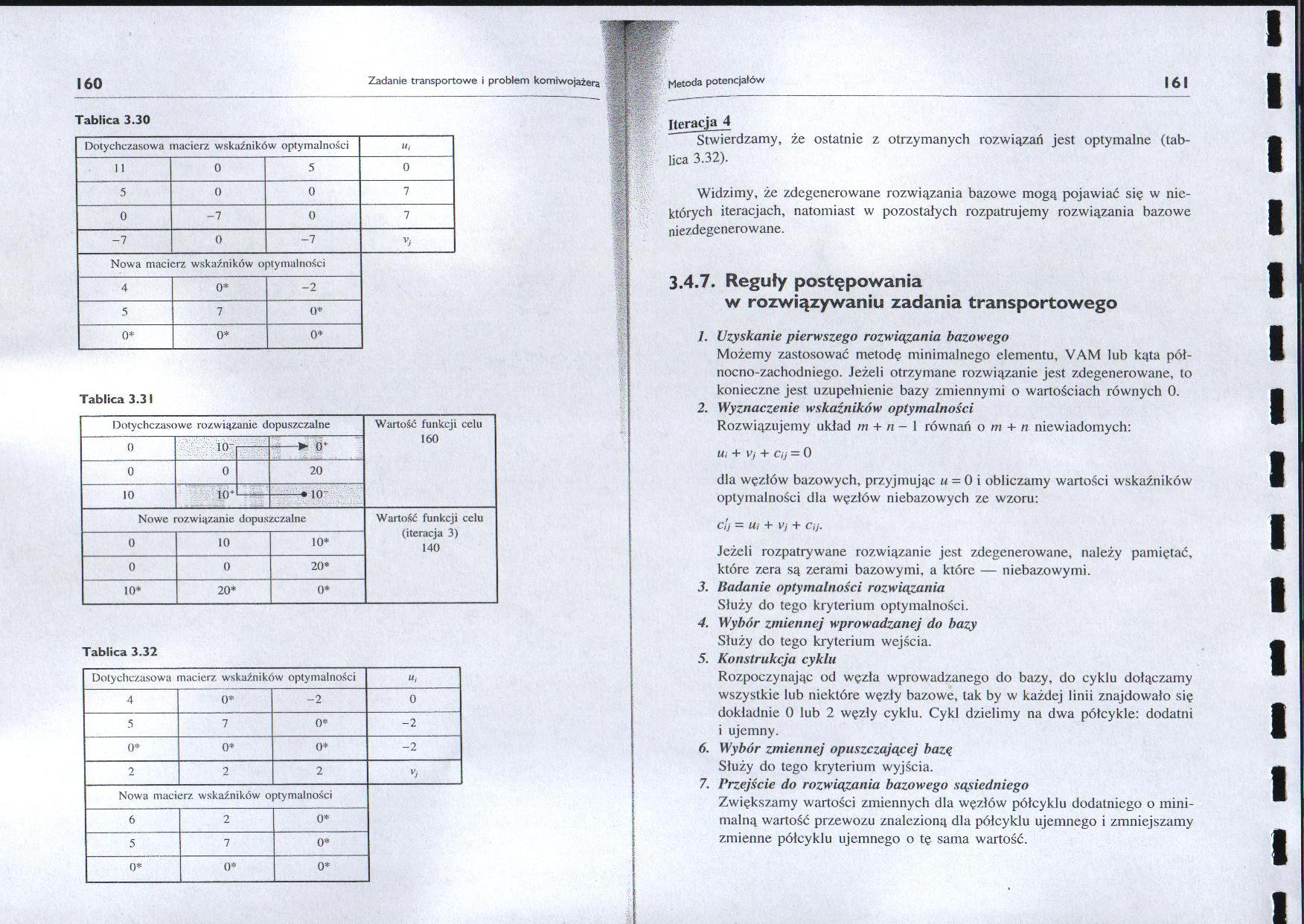
Tablica 3.30

Dotychczasowa macierz wskaźników oplyrnalności			U ,■
11	0	5	0
5	0	0	7
0	-7	0	7
-7	0	-7	^vi
Nowa macierz wskaźników oplyrnalności
4	0*	-2
5	7	0*
0*	0*	0*

Tablica 3.31

Dotychczasowe rozwiązanie dopuszczalne				Wartość funkcji celu 160
0	10		--► 0*
0	0		20
10	10^ł		——• 10'
Nowe rozwiązanie dopuszczalne				Wartość funkcji celu (iteracja 3) 140
0	10		10*
0	0		20*
10*	20*		0*

Tablica 3.32

Dotychczasowa macierz wskaźników oplyrnalności			U;
4	0*	-2	0
5	7	0*	-2
0*	0*	0*	-2
2	2	2	^vi
Nowa macierz wskaźników optymalności
6	2	0*
5	7	0*
0*	0*	0*

Iteracja 4

Stwierdzamy, że ostatnie z otrzymanych rozwiązań jest optymalne (tablica 3.32).

Widzimy, że zdegcncrowane rozwiązania bazowe mogą pojawiać się w niektórych iteracjach, natomiast w pozostałych rozpatrujemy rozwiązania bazowe niezdegenerowane.

3.4.7. Reguły postępowania

w rozwiązywaniu zadania transportowego

1.    Uzyskanie pierwszego rozwiązania bazowego

Możemy zastosować metodę minimalnego elementu, VAM lub kąta północno-zachodniego. Jeżeli otrzymane rozwiązanie jest zdegenerowane, to konieczne jest uzupełnienie bazy zmiennymi o wartościach równych 0.

2.    Wyznaczenie wskaźników optymalności

Rozwiązujemy układ m + n — 1 równań o m + n niewiadomych:

u, + Vj + dj = 0

dla węzłów bazowych, przyjmując u = 0 i obliczamy wartości wskaźników optymalności dla węzłów niebazowych ze wzoru:

c!j = u, + Vj + Cij.

Jeżeli rozpatrywane rozwiązanie jest zdegenerowane, należy pamiętać, które zera są zerami bazowymi, a które — niebazowymi.

3.    Badanie optymalności rozwiązania Służy do tego kryterium optymalności.

4.    Wybór zmiennej wprowadzanej do bazy Służy do tego kryterium wejścia.

5.    Konstrukcja cyklu

Rozpoczynając od węzła wprowadzanego do bazy, do cyklu dołączamy wszystkie lub niektóre węzły bazowe, tak by w każdej linii znajdowało się dokładnie 0 lub 2 węzły cyklu. Cykl dzielimy na dwa półcykle: dodatni i ujemny.

6.    Wybór zmiennej opuszczającej bazą Służy do tego kryterium wyjścia.

7.    Przejście do rozwiązania bazowego sąsiedniego

Zwiększamy wartości zmiennych dla węzłów półcyklu dodatniego o minimalną wartość przewozu znalezioną dla półcyklu ujemnego i zmniejszamy zmienne półcyklu ujemnego o tę sama wartość.