124 2

246 XI. Szeregi potęgowe
Rozwijamy prawą stronę w szereg potęgowy:
y' = l-x2+x4-x6 + ...
skąd
ostatecznie
Szereg ten jest zbieżny, gdy x2< 1, tzn. gdy h<l. Całkując ten szereg wyraz po wyra^e otrzymujemy
|
arctg x = |
7 x5 |
x7 | |
|
* 3+5 |
7 +' |
’ • 9 | |
|
1 / /iN |
\3 |
l5 l( |
h\\ 1 |
|
n7, |
* n |
v +-J | |
|
[h 1 |
(h V |
V*Y+ i | |
|
L1 3 |
W +7< |
w |
7 w "J |
Wzór ten daje rozwiązanie zadania, gdy h<l. W przypadku gdy h=l, mamy s=nl.
Zadanie 11.23. Pozioma skala przyrządu pomiarowego odbija się w lusterku zawieszonym na osi pionowej w odległości s od skali; odbicie to obserwujemy przez lunetkę. W chwili gdy lusterko jest równoległe do skali, widzimy przez lunetkę punkt 0 skali. Odchyleniu lusterka o kąt (p odpowiada na skali odchylenie liniowe a. Dla jakich kątów <p (podać w stopniach) można przyjąć zależność tpvkx z błędem względnym nie przekraczającym 1%?
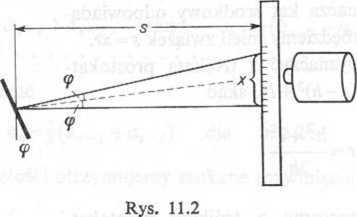
Rozwiązanie. Gdy lusterko odchyla się o kąt (p, promień widzenia odchyla się o kąt 2(p (patrz rys. 11.2). Mamy tg a=tg 2<p=x\s, skąd
1 *
<p=± arctg — s
Oznaczmy x'js=t. Wówczas ę = \ arctg t. Rozwijamy funkcję arctg t w szereg
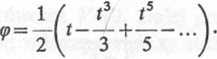
V\' przybliżeniu można wziąć q> = \t, czyli
1 x
Błąd bezwzględny A<p można ograniczyć nierównością Aę<ł-$t3, a wówczas błąd względny spełnia nierówność A<plcp<\t2, czyli
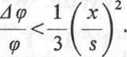
^by błąd względny był mniejszy od 1 %, należy wziąć ^ tg21<~, czyli t<0,173, a więc ę< 0,0865.
W stopniach otrzymujemy wzór
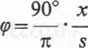
z błędem nie przekraczającym 1%, jeżeli <p< 5°.
Zadanie 11.24. Obliczyć sin 5 z dokładnością do 0,0001, posługując się rozwinięciem funkcji sin x w szereg potęgowy.
Rozwiązanie. Rozwinięcie daje
357 X X X
sin x=x---1------h...
Szereg jest przemienny, zbieżny.
Przy obliczeniu sin można się ograniczyć do dwóch wyrazów:
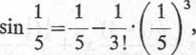
gdyż popełniony błąd będzie mniejszy od wyrazu
5! V 5/ 375000
Obliczenie daje sin | = 0,2-0,0013=0,1987.
Przy obliczeniach numerycznych dochodzi błąd zaokrąglenia, który łącznie z poprzed-błędem jest mniejszy od 0,0001.
Zadanie 11.25. Obliczyć wartość 1 /e z dokładnością do 0,001, posługując się rozwinię-tle® funkcji ex w szereg Maclaurina.
Rozwiązanie. Rozwinięcie funkcji ex w otoczeniu punktu x0 =0, jak wiemy, jest następujące:
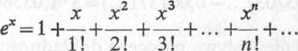
Wyszukiwarka
Podobne podstrony:
246 XI. Szeregi nieskończone o wyrazach stałych Sumując je od k = 1 do k = n otrzymamy ogólny wyraz
423 § 4. Dodatkowe wiadomości o szeregach potęgowych Rozwińmy teraz lewą i prawą stronę według potęg
117 2 232 XI. Szeregi potęgowe Jest to wniosek z kryterium d Alemberta zbieżności szeregów. (11.1.4)
118 2 234 XI. Szeregi potęgowe Zadanie 11.4. Znaleźć promień zbieżności szeregu potęgowego “ n"
120 2 238 XI. Szeregi potęgowe Zadania 239 238 XI. Szeregi
240 XI. Szeregi potęgowe czyli po uporządkowaniu: 1 1 1-3 = l--xH——rx — 2 2!
122 2 242 XI. Szeregi potęgowe ie/(0) = 0, otrzymujemy .2 2 2 23 4 25 6 27 .S,n *= 27 * _47 * +óT *
244 XI. Szeregi potęgowe Rozwiązanie. Zakładamy, że x^0 i x^3. Postępujemy podobnie jak w
125 2 248 XI. Szeregi potęgowe Zadania 249 Dla x — — 1 otrzymujemy 1 11111 (-1)" Jada
250 XI. Szeregi potęgowe “ u3+5""•"5- .5,^ “ n! „ 11.47. £ -55 *• n = 0 # oo n—
127 3 252 XI. Szeregi potęgowe Zadania 253 l+x+x- g Rozwinąć w szereg Taylora funkcje (zad. 11.92 -
image 037 Podsumowsmie 37 Analogicznie, dla sytuacji z rys. l.lOb, możemy zapisać prawą stronę
skanowanie0003 Wskazówki zegara zawsze przesuwają się w prawą stronę. Ruch ten nazywamy ruchem wskaz
więcej podobnych podstron