123

244 XI. Szeregi potęgowe

Rozwiązanie. Zakładamy, że x^0 i x^3. Postępujemy podobnie jak w poprzednią

zadaniu:

-^—=a₀+a₁(x~2)+a₂(x-2)²+a₃(x-2)³+.„ x — 3x

Oznaczmy x-2 = u, skąd x=u+2, i otrzymujemy

(u + 2) + 2    2    3

^ao + aiU + flzM +«3«+...»

(u +2)² —3(h +2)

gdzie -2 i u<£ 1 ze względu na zastrzeżenia co do wartości x. Po redukcji mamy

czyli

u +4    j ,

■ = a₀ + a_lu+a₂u +a₃u +.

u^z+w-2

4+u=(-2+u +u²)(a₀ + a₁u + a₂ u²+a₃u³ + ...).

Przyrównując współczynniki przy jednakowych potęgach zmiennej u po obu stronach otrzymujemy:

0 a CS 1 11	skąd	a0 — "~2,
l = -2a1 + «0»	skąd	ł-* 11 l MW
0= —2 a2+a2 +a0 >	skąd	1 II <3
0= —2fl3 + fl2'ł*®i»	skąd	„ ^13 ^3 8 ^9
0= —2afl+an_1+on_2,	skąd	^ = l(^a»-l+an-2)r

Zatem wzór ogólny ma postać

0*=4(«/.-i + «n-2) dla n> 2.

Podstawiając powyższe wartości otrzymujemy szukane rozwinięcie

Można wykazać, że szereg ten jest zbieżny dla \x—2|< 1, czyli w przedziale zbieżność l<x<3.

Zadanie 11.21. W kulę o promieniu r wpisane są dwa stożki mające wspólni® i wspólną podstawę o promieniu a. Wyznaczyć różnicę V objętości tych stożków i w) zić ją za pomocą szeregu potęgowego względem ajr.

Rozwiązanie. Gdy a=r, wówczas V=0. Dalej przyjmujemy a<r Oznaczmy ^ sokość mniejszego stożka przez h; wówczas większy stożek będzie miał wysokość 2r

gd^ie h<r. Różnica objętości stożków wynosi ^uważmy, że r² = a² + (r-h)², skąd

V = \na²(2r — h)—\na²h=\na²(r—K).

r-h = \Ir² — a². Wielkość V można napisać w postaci

K = f 7ta²r(l+x)*, gdzie x=-^—

Rozwijając funkcję y=(l +x)^ł według wzoru Maclaurina otrzymujemy

a+^^ł= t ay,

k~0 \ K /

gdzie -l<x<0. Stąd

V=\na²r

[\ V^1	“V ^xi	1- CS CS
L^1' 2\-	r) 8 (	<rj 16\r) -J

Zadanie 11.22*. Wyznaczyć długość łuku s okręgu jako funkcję długości / połowy cięciwy ściągającej dany łuk i jego strzałki h (rys. 11.1).

Otrzymaną funkcję rozwinąć w szereg potęgowy względem ilorazu h/l. •

Rozwiązanie. Mamy daną cięciwę 21 i strzałkę łuku h. Oznaczmy przez r promień okręgu, do którego należy łuk s, i niech a oznacza kąt środkowy odpowiadajmy łukowi s. Wówczas będziemy mieli związek s=ar.

Promień r można wyznaczyć z trójkąta prostokątnego ODA; mamy r² = (r — h)² +1², skąd

(1)

h² + l²

r—-

2h

Nati

^;omiast kąt a wyznaczmy z trójkąta prostokąt-

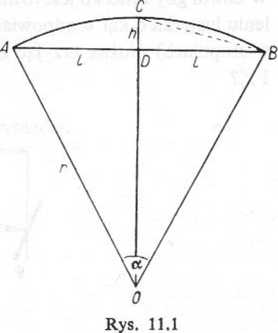
•^eg° BCD, w którym j:CBD = ±a. Otrzymujemy związek tg $<x=h/l, skąd (2) • ^h

|a = arctg —•

%li,

Oznaczając hjl=x, $x=y otrzymujemy związek

y = arc tg x.

^Czamy pochodną

,

k =

1

l+x

2 '