150(1)

Wszystkie punkty nieciągłości funkcji dwóch zmiennych z = f(x, y) tworzą zbiór punktów nieciągłości. Jeżeli zbiór ten przedstawia pewną linię, nazywamy ją linią nieciągłości funkcji.

Na przykład funkcja z —    ^ jest nieciągła w każdym punkcie

i x y

okręgu x¹+y¹ = 1. Okręg ten jest właśnie linią nieciągłości danej funkcji. 716. Wyznaczyć granice:

717. Wyznaczyć punkty i linie nieciągłości funkcji:

§ 3. Pochodne cząstkowe funkcji wielu zmiennych

Funkcję u —f(x,y. z, ..., t) można różniczkować względem każdego z argumentów, traktując przy tym wszystkie pozostałe argumenty jako stałe.

Pochodną funkcji u =f(x,y, z,...,/) względem x, wziętą przy założeniu, że pozostałe jej argumenty y, z, t są stałe, nazywamy pochodną cząstkową u względem x i oznaczamy symbolem 4^- albo u'_x. Zatem

f(x-r Ja% y, z, .... /) -f(x, y. z, ..., t)

J.Y

Analogicznie określa się i oznacza pochodne cząstkowe funkcji u względem każdego z pozostałych jej argumentów.

Przy obliczaniu pochodnych cząstkowych funkcji wielu zmiennych obowiązują reguły poznane przy różniczkowaniu funkcji jednej zmiennej (rozdz. II).

718. Obliczyć pochodne cząstkowe funkcji:

Analogicznie, traktując z tylko jako funkcję y, otrzymamy ' =

cy

— 10xy—3y².

2)    Zakładając kolejno, że u jest funkcją tylko .y, potem tylko y, a następnie tylko z, otrzymamy

du _ I z cu _ x 1 du _ y 1

dx y ' X² ’ dy y² 1 z ’ dz z² x

3)    Zastępując pierwiastek potęgą o wykładniku ułamkowym, a następnie różniczkując względem każdej z obu zmiennych, otrzymamy

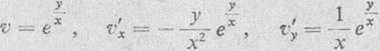
719. Obliczyć wartości pochodnych cząstkowych funkcji dla wskazanych wartości argumentów:

1) /(a, £) = cos(w«—w/9);    a =    /3 = 0

2) z = ln(.Y²-/);    -V = 2. p=-l

Rozwiązanie: 1) Stosując odpowiednie reguły różniczkowania (rozdz. II), znajdujemy pochodne cząstkowe

fa— -m sin (ma— nfi), fp = /;sin(ma—nfi)

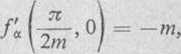
7Z

Podstawiając a—    fi — 0, otrzymujemy

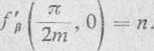
2.y

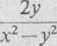
303

1

Rozwiązanie: 1) Traktując z jako funkcję jednego tylko argumentu

dz

x, w myśl reguł rozdz. TI,znajdujemy .    — 3.v¹ • 5y³.

2

Znajdujemy pochodne cząstkowe, a następnie obliczamy ich wartości szczególne we wskazanym punkcie

3

z = x³-\-5xy¹—y¹    2) « = — -h —— —    3) v = i e^y

y z x