159 2

Metody doboru nastaw regulatorów 159

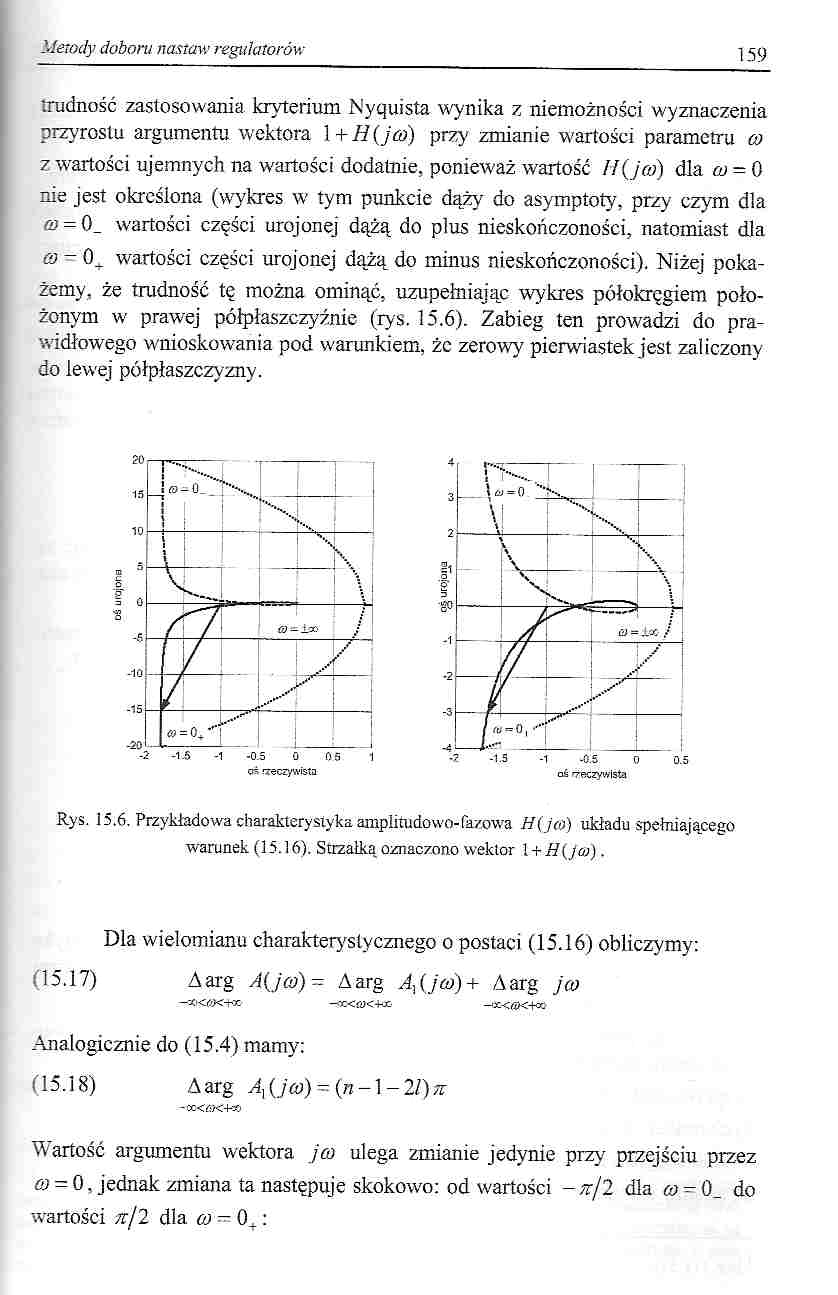
trudność zastosowania kryterium Nyąuista wynika z niemożności wyznaczenia przyrostu argumentu wektora 1 + H (jco) przy zmianie wartości parametru co z wartości ujemnych na wartości dodatnie, ponieważ wartość ff(jco) dla oj - 0 nie jest określona (wykres w tym punkcie dąży do asymptoty, przy czym dla co = 0_ wartości części urojonej dążą do plus nieskończoności, natomiast dla 0-0. wartości części urojonej dążą do minus nieskończoności). Niżej pokażemy, że trudność tę można ominąć, uzupełniając wykres półokręgiem położonym w' prawej półpłaszczyźnie (rys. 15.6). Zabieg ten prowadzi do prawidłowego wnioskowania pod warunkiem, żc zerowy pierwiastek jest zaliczony do lewej półpłaszczyzny.

Metody doboru nastaw regulatorów 159

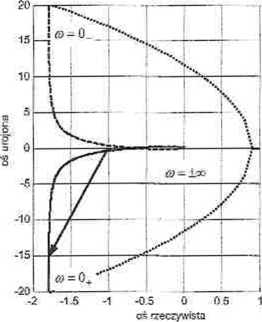
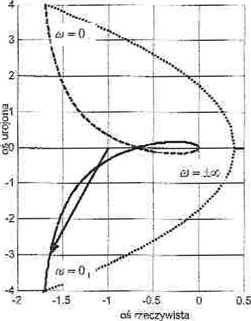
Rys. 15.6. Przykładowa charakterystyka amplitudowo-fazowa H(j<d) układu spełniającego warunek (15.16). Strzałką oznaczono wektor 1 + H{jai).

Dla wielomianu charakterystycznego o postaci (15.16) obliczymy:

(15.17)    Aarg A(jco)- Aarg A, (joj) + Aarg jco

—*<OX-rX,    -oc<<y<4-x-    -oc«5K-H»

Analogicznie do (15.4) mamy:

(15.18)    Aarg A_}(jco) ~(n-]-21)n

-OCCrtK+oO

Wartość argumentu wektora jco ulega zmianie jedynie przy przejściu przez 0 = 0. jednak zmiana ta następuje skokowa: od wartości —njl dla co~ 0_ do wartości zr/2 dla co — 0₊: