CCF20091206013

Przykłady

Przykład 2.1. Obliczyć pracę w układzie zamkniętym, którego energia wewnętrzna uległa zmianie od wartości U, = 5000 kJ do wartości U₂ = 4000 kJ, jeśli z zewnątrz zostało doprowadzone ciepło Q_t 2 =i = 6000 kJ.

Rozwiązanie

Zgodnie z pierwszą zasadą termodynamiki bilans energetyczny układu ma następującą postać

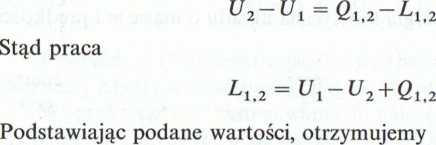
L_U2 = 5000-4000 + 6000 = 7000 kJ

P

1

p-V

Ponieważ znak pracy jest dodatni, została ona przez układ wykonana.

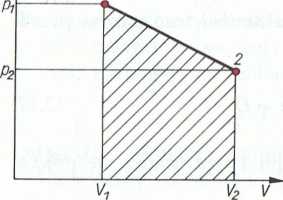
Przykład 2.2. Czynnik gazowy zamknięty w cylindrze podlega przemianie, której wykresem w układzie współrzędnych ciśnienie — objętość (p-V) jest odcinek linii prostej (rys. 2.8). Parametry czynnika w punkcie początkowym przemiany wynoszą

luk widać na rys. 2.8, pole przedstawiające pracę bezwzględną w ukła--l/ln p-V jest trapezem, a więc

£1.2 = ^(P₁+P₂)(V₂-V₁) = y (0,4 • 10⁶+

+ 0,25-10⁶)-(0,5-0,2) = 97 500 J = 97,5 kJ

\ _v \ \

ri/ykłaJ 2.3. Winda o masie 2000 kg pozostaje w spoczynku na w ysokości h_t = 8 m powyżej dna szybu. Następnie zostaje wciągnięta na w ysokość h₂ = 80 m. W tym momencie pęka lina wciągowa i winda umila swobodnie na dno szybu, gdzie zostaje wyhamowana przez silną piężynę. Układ hamujący jest wyposażony w blokady sprawiające, że winda pozostaje w położeniu maksymalnego ugięcia sprężyny. Za-k lądując, że całe zjawisko przebiega bez strat, obliczyć: a) energię potencjalną windy w jej początkowym położeniu względem dna szybu; h> energię potencjalną windy w jej najwyższym położeniu względem dna u/ybu; c) pracę wykonaną na podniesienie windy; d) energię kinetyczną 1 prędkość windy tuż przed uderzeniem w sprężynę; e) energię potencjal-iii| całkowicie ugiętej sprężyny; f) energię układu składającego się / windy i sprężyny w stanie: 1 — w chwili początkowej, 2 — gdy winda usiąga najwyższe położenie, 3 — tuż przed uderzeniem windy o sprężynę; 4 — po zatrzymaniu się windy na dnie szybu.

Rozwiązanie

11) E_p{ = mg(h_l —h₀) = 2000-9,81 -8 = 156 960 J = 156,96 kJ

li) E_p2 = mg(h₂ — h₀) = 2000-9,81-80 = 1 569 600 J = 1569,6 kJ

1) Pierwsza zasada termodynamiki — wzór (2.17) — redukuje się do

Ep — ~

ponieważ AU = 0; AE_k = 0; Q_t 2 = 0.

Stąd

Li 2 = E_pl-E_p2 = 156,96-1569,6 = -1412,64 kJ

d) Proces swobodnego spadania między stanami 2 i 3 odbywa się bez Ntrat, zatem L₂ 3 = 0. Ponadto <2₂,₃ = 0.

Pierwsza zasada termodynamiki przyjmuje postać

AE_kx 3 + AE_P23 = 0, czyli    E_ky - E_k2 + E_p3 - E_pi = 0.

Rys. 2.8. Wykres przemiany w układzie p₁ = 0,4 MPa i V₁ = 0,2 m^{1 2 3}, a W pun-

kcie końcowym p₂ = 0,25 MPa

41

1

V₂ = 0,5 m³. Obliczyć pracę bezwzględną wykonaną podczas przemiany.

2

Rozwiązanie

3

Praca bezwzględna L_{ 2 wykonana podczas przemiany jest równa polu powierzchni zakreskowanemu na rys. 2.8, które wyznaczają punkty Pj, 1, 2 i V₂.