DSC07348
5
Geometria analityczna w przestrzeni
Przykłady
• Przykład 5.1
Obliczyć długości podanych wektorów:
a) 5= (1,-71,^5); b) PQ, gdzie P = (1,2,3), Q = (4,6,15).
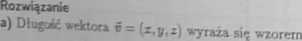
151 = \A* + (-^)ł + (>/6)* = y/9 = 3.
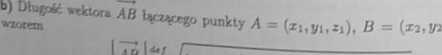
= B = wyr8Żn'
Zatem ^ ^ “*»)* + Cltt - ył)a + (xj - n)a.
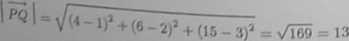
Przykłady
115
• Przykład 5.2
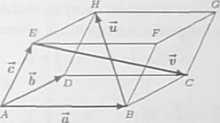
Równoległościan jest rozpięty na_ wektorach 5, 6, c. Wyrazić przekątne tego rów-nolcglościanu przez wektory a, 6, c.
Rozwiązanie
Niecił u =BH, v =EC, iu =AG i z =DF oznaczają przekątne równoległośdanu rozpiętego na wektorach 5, 6, S (rysunek). Aby nie zaciemniać rysunku zaznaczono na nim tylko dwie przekątne Si ii. Z faktu, że łamana ABHEA jest zamknięta wynika równość 3+5 = c+6, stąd 5= c + 6 — 5. Podobnie z faktu, że łamana ABCEA jest zamknięta wynika równość 5 + 6 = c + 3, stąd 3=5+6 — c. Z analogicznych rozważań wynika, że trzecia przekątna ui wyraża się wzorem Si = 5 + 6 + 0, zaś czwarta 2 = 5—6+2.
• Przykład 5.3
Znaleźć dowolny wektor u, który z wektorami 5 = (1,2,3), 6 = (6,—4,2) tworzy jednakowe kąty i leży w płaszczyźnie wyznaczonej przez te wektory.
Rozwiązanie
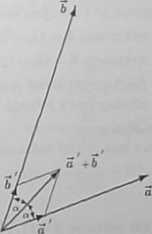
W rozwiązaniu wykorzystamy fakt mówiący, że wektor, który jest sumą dwóch wektorów o jednakowych długościach, tworzy z nimi jednakowe kąty i leży w płaszczyźnie wyznaczonej przez te wektory. Fakt ten wynika z elementarnych własności rombu. Niech a i b oznaczają wektory jednostkowe równolegle (z zachowaniem zwrotu) odpowiednio do wektorów a i 6 (rysunek). Wtedy
imm____(i.2,_?)____f_i_ 2 _3_\
|5| Vla + 21 + 32 \y/Ti' y/UJ ' K'_ 6 _ (6,-4,2) _ f 3 -2 1 |
|b| y/S1 + (—4)3 -+2* \y/u'y/WVU,J
Wektor u tworzący jednakowe kąty z wersorami 5,6 , a zatem takie z wektorami 6, ma postać
a i
5= a'
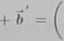
Wyszukiwarka
Podobne podstrony:
DSC07349 116 Geometria analityczna w przestrzeniIloczyn skalamy • Przykład 5.4 Obl
x148 RACHUNEK WEKTOROWY Zad.l. Obliczyć długości podanych wektorów.: a) o* = (3,-4
126 Geometria analityczna w przestrzeni 0 Zadanie 11.8 Obliczyć pola podanych powierzchni: a)
126 Geometria analityczna w przestrzeni 0 Zadanie 11.8 Obliczyć pola podanych powierzchni: a)
DSC07360 138Geometria analityczna w przestrzeniPP= (1 — x, —y, —3 — z) Wektor PP jest prostopadły do
4. GEOMETRIA ANALITYCZNA W PRZESTRZENIDhjpcic wektora *.» - [*x. -7,vJ i a>>mu>y k*.smnkowe
DSC07362 142Geometria analityczna w przestrzeni dla pewnego UR{0}. Mamy fi = (1,1,1) oraz SP= (-z, 1
Dynamika JS analitycznai «MATHEMATICA» w zadaniach i przykładach obliczeniowych ksiazka.edu.pl Oficy
DSC07356 130Geometria analityczna w przestrzeni Potrzebny jest jeszcze dowolny punkt P należący do p
DSC07308 WielomianyPrzykładyPodstawowe definicje i własności • Przykład 2.1 Obliczyć iloczyny podany
7. Obliczyć długości podanych krzywych: «) y = ln e-r _ r x e I2,3); 6) *-?5 + £’ *€M; c)
DSC07363 144 Geometria analityczna w przestrzeni • Przykład 5.22 Obliczyć objętości i pola powierzch
DSC07350 118 Geometria analityczna w przestrzeni jest równoległa do wektora Rzut prostokątny dowolne
DSC07351 120 Geometria analityczna w przestrzeni • Przykład 5-9 Obtarć odległość punktu P = (3,2,5)
DSC07357 132 Geometria analityczna w przestrzeni wspólliniowc. Wektor normalny rti płaszczyzny iri :
DSC07364 146 Geometria analityczna w przestrzeni • Przykład 5.24 Punkty A = (0,0,0), B = (4,0,0), C
DSC07368 154 Geometria analityczna w przestrzeni • Zadanie 5.8 Obliczyć pola podan
więcej podobnych podstron