DSC07349

116

Geometria analityczna w przestrzeni

Iloczyn skalamy

•    Przykład 5.4

Obliczyć iloczyny skalarne podanych par wektorów:

a) 5 = (-1,5,2), b = (3,0,7); b) H-i-j+k, v = 3i-2k.

Rozwiązanie

a)    Iloczyn skalamy wektorów a = (2x.y1.-1), b = (23,2/3,23) obliczamy ze wzoru

Soi = 2123 + 2/12/2 + 2x23.

Zatem

ao{ = (-1,5,2)o (3,0,7) = (-1) - 3 + 5 0 + 2 - 7 = 11.

b)    W rozwiązaniu wykorzystamy własności iloczynu skalarnego wektorów oraz fakt, że weisory i, j, £ są parami prostopadle, tzn. spełniają równości:

ia j = jo k = k o i = 0.

Zatem

fi o fi = (?-J+ jfc)o(3t-2£)

= 3(ioi) —2 (i o £)— 3(Joi) + 2(jofc)+3(fcoi)- 2 (fco £)

= 3-2=1.

Uwaga. Przykład b) można oczywiście obliczyć tak jak a) zapisując fi = (1,—1,1), 9 = (3,0,-2).

•    Przykład 5.5

Korzystając z iloczynu skalarnego obliczyć miary kątów między:

a)    wektorami 5= (l,%/2,3) , 5 = (0,—>/2, l) ;

b)    wektorem u = (4,—12,3) i płaszczyzną xOz układu współrzędnych;

c)    przekątnymi ścian prostopadłościanu o krawędziach a = 5, b = 6, c = 7, wychodzącymi z jednego wierzchołka.

Rozwiązanie

Miara kąta między wektorami niezerowymi fi i 5 wyraża się wzorem

Ą. (o, i) = arc<

do b

W-W

a) Dla wektorów fi = (l, v/5,3) i 5 = (0,-\/2, l) mamy

(i. vf,3)o(0,->/2, Ł)

^ ( 3, 6) = arct

+ (V^)³ + 3* ^0* + (-t/2)* + 1*

= iiccmt =55 l,40(rad| =; 80,4' o

Przykłady

117

b) Zauważmy najpierw, że miara kąta między wektorem i płaszczyzną jest równa mierze kąta między tym wektorem i jego rzutem prostokątnym na tę płaszczyznę. Rzut prostokątny wektora u = (4, —12,3) na płaszczyznę xOz ma postać u = (4,0,3). Zatem

: =<. (u. u ^ = arccos

(4,-12,3) o (4,0,3)

+ 0* + 3* _r V⁴* ⁺ Hf + ^3ł

= arccos — ~ 1,18[rad| ss 67,3°.

Id

c) Sytuację omawianą w zadaniu przedstawiono na rysunku poniżej. Początek układu współrzędnych umieszczono w jednym z wierzchołków prostopadłościanu, a osie pokrywają się z jego krawędziami. Wektory fi, 6 i w rozpinające ten prostopadłościan mają wtedy postać:

fi = (o, 0,0) = (5,0,0),    3 = (0.6,0) = (0,6,0), u) = (0,0, e) = (0,0,7).

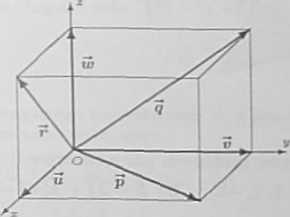
Przekątne ścian prostopadłościanu wychodzące z początku układu współrzędnych są reprezentowane przez wektory:

P = 5+3 = (5,6,0), q = 3+tu = (0,6,7), ?= fi+ w = (5,0,7).

Miary kątów między tymi przekątnymi wyrażają się wzorami:

$ (P< 9) = arccos _T j*. °-= arccos

IpI - kl

^ (rj, P) = arccos

(a, 6.0) o (0,6,7)    36

•JS¹ -t-6^J • V6^r+7^T    >/5185

- - -    (5.6.01    o    fó.0.7)    25

-1= arccos — _    '—i    ' . = arccos ; —

V5^J + 6³ - V5^a + 7»    x/4514

40

.60°

=3 68°,

lai-m

(0.6,7) o (5.0,7)

-^arceos:

s 52°.

• Przykład 5.6

Obliczyć długość rzutu prostokątnego wektora 3 = (3,4,-1) na prostą tworzącą jednakowe kąty z dodatnimi osiami układu współrzędnych.

Rozwiązanie

Zauważmy najpierw, że prosta tworząca jednakowe kąty z osiami układu współrzędnych