DSC07369

156

Geometria analityczna w przestrzeni

_ . - ₊ 2y- = +-l = ⁰'    / 2x-._/-2= + 8 = 0,

a) prostych li : j y + z — 3 = 0,    \ x + -U + 2; - 5 — 0;

I u , o . _ 4 x - 1 V'^r- =- i płaszczyzny

b) prostej I: —jj--3    -1

f x = 3 + t,

J p = l + a + 2!, gdzie s,!€R;

Ki _r = 3 + 2s + 4!,

= 0.

c) płaszczyzn : 3x+y+?+1 = 0, ir₂ : *+2z + 6 = 0, tt₃ : 3p + 2z

• Zadanie 5.17 Obliczyć odległość:

= 0;

+ 4z = 0.

a)    punktu P = (1,-2,3) od płaszczyzny ir : x + y-3z + 5 = 0;

b) płaszczyzn równoległych irj : 2x + y — 2z = 0,?r₂ : 2x + y — 2z — 3

c) płaszczyzn *i : x — 2p + 2x + 5 = 0, sr₂ : 3x — 6p + 6z — 3 = 0;

x y z

	_1/+1 _	— 1,	x p-1
	2	—1' ■'	-2 -4
f x = 0,	, . f * =	1,
l v=o.	^,2‘ 1 «-	i;
p-2 z		p + 7_	z-2
-3 1'	-2	9	1 2 ■

z-3 2 '

[ x = 2 ft,

h) prostej 1: < y — — 3 + 21, gdzie 1 6 R, od płaszczyzny ir : 2x + y

d)    punktu P = (0,1, -1) od prostej l: ^

e)    prostych równoległych lj:

g)    prostych li : —-

• Zadanie 5.18

Obliczyć miarę kąta między: i _    z —3    u — 1 z + 2

aj prostą /:    ₂    ~ ⁼ "Z-f ‘ płaszczyzną ir: x - z = 0;

b)    płaszczyznami w, :_X-2p + 3z-5 = 0.x₂:2z+«-_{2 +} 3 _{= 0}.

I * — 1 ■*(,    f Z&3    '

gdzie 1 £ R-

c)    prostymi!,: Ł p = -2 + !, gdzie! 6 R, l₂| i    '

1 * = 1 + 3!,

• Zadanie 5.19 Znaleźć rzut prostokątny:

a)    punktu P = (-3.2,0) na płaszczyznę z : x + p + z = 0;

c) prostej 1:

b)    punktu P = (-1,2.0) na prostą 1: x = p = z; ^z~³_ P-5 z + 1

1    5~ = -q—na płaszczyznę w: x + 3p-2z_ 0 = 0.

Zadania

157

• Zadanie 5.20

Znaleźć punkt symetryczny do punktu P = (2,3, -1) względem:

a) punktu S = (1,—1,2);

i , .. / i +t/ = 0,

b)    prostej l: j _{y + ; = 0;}

c)    płaszczyzny 7r: 2x - y + z — 6 = 0.

•    Zadanie 5.21

Znaleźć rzut ukośny w kierunku wektora v = (2,3, — 1):

a)    punktu O = (0,0,0) na płaszczyznę <r: x — 2z + 8 = 0;

b)    prostej l: x — 1 = -I-1 = z — 2 na płaszczyznę ir: x — y + z — 1=0.

•    Zadanie 5.22

Obliczyć objętości i pola powierzchni brył ograniczonych podanymi płaszczyznami:

^a) * = l. 11 =-1, s = 3,i + y+z = 5;

b) z-y= I,s-y = 5, a: + 2z = 0, x + 2z = 3, z =-1, z = 4.

* Zadanie 5.23

Obliczyć pole trójkąta utworzonego przez parami przecinające się proste:

i = 0,    ( x = —2p,

y = 3 + 3s, I3 : < y = 3 — 3p, gdzie t,a,p 6 R. z = —4a,    l z = 0,

I r = -2 + 2t, k ■ s y — 0, l_a ; I z = 4t.

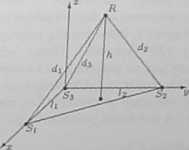
• Zadanie 5.24

Stacje radiolokacyjne Si, Sn., S3 umieszczone są w wierzchołkach trójkąta prostokątnego o przyprostokątnych /, = 300 km, l₃ = 400 km (rysunek). Pomiary odległości rakiety R od tych stacji dały następujące wyniki dj = 300 km, da = 400 km, d₃ = 400 km. Obliczyć, na jakiej wysokości h leciała rakieta.

! Zadanie 5.25

Cząsteczka porusza się po linii prostej ze stałą prędkością. W chwili t, = 2 cząsteczka znajdowała się w punkcie Pi = (0, —2,5), a w chwili tj = 3 w punkcie P₃ = (2,3,3). Znaleźć położenie Pa tej cząsteczki w chwili to = 0.

Zadanie 5.26

Na pochyłym pińskim terenie wytyczono kwadrat AiA₃A₃Aą. Wzniesienia nad poziom morza punktów/li, A₃, A3 wynoszą odpowiednio hi = 100m, h₃ = IlOm,

h = 160m. Obliczyć wzniesienie /i« punktu At nad poziom morza.