DSC07358

134

Geometria analityczna w przestrzeni

Znajdziemy ima punkt P przecięcia prostej i i płaszczyzny ir. Współrzędne tego punktu [spełniają układ równań

2x - y - 2= = 0, x- I _ y+ 1 _ z - 3

a ‘ -a * |

Po rozwiązaniu tego układu otrzymamy x — y = —z = Obliczamy teraz odie-

głoeć d punktu P = . -J od punktu P = (0,0,0), czyli szukaną odległość punktu

P od prostej Ł mamy

KT -V(!-o)’-H-°)Ml-°r-4^**

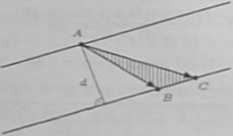
d) I sposób. Odległość d między prostymi równoległymi li 1 /a wyznaczymy w następujący sposób: na prostej li wybieramy dowolny punkt /l, a na prostej li dwa dowolne punkty B. C; obliczamy pole S trójkąta ABC (wykorzystując iloczyn wektorowy); obliczamy wysokość tego trójkąta opuszczoną z wierzchołka A.

■a

Aby wyznaczyć dowolny punkt A na prostej

/, - ^x ~ ¹ J g ~ ² ₌ £+3

przyjmujemy x = I. stąd y = 2 oraz t = —3. Zatem A = (1,2, —3). Podobnie znajdujemy ptmfczy BiCna prestej /j : - = - = Przyjmując x = 0, otrzymamy y = 0 oraz z = 0, a przyjmując x = I. otrzymamy y = 2 oraz z = 3. Zatem B = (0,0,0), C = (1,2,3). Obliczamy teraz pole S trójkąta ABC korzystając ze wzoru

S= || AB x AC |

Tak więc mamy

5 = jK-I. -2 3) * (0.0,6)| = i|(-12.6.0)| = ią/(-12)> + aa+(P = 3>/5.

Obliczamy rantąpne długość boku BC trójkąta ABC. Mamy

\BC\ = y/(l -0)> + (2-0)> + (3 —0)> = VT4.

Możemy teraz obliczyć wysokość trójkąta A/łC opuszczoną z wierzchołka A, czyli szukaną odległość d prostych li i Ig. Mamy

2-3v/5 3

. 25

Przykłady

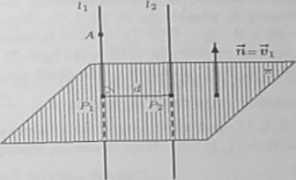
II sposób. Odległość <i między prostymi równoległymi li i ta obliczymy w następujący sposób: wyznaczymy równanie płaszczyzny w prostopadłej do obu prostych (przechodzącej przez dowolny punkt Pi na prostej l\), następnie wyznaczamy punkt ft przecięcia tej płaszczyzny z prostą () i na końcu obliczamy odległość punktów Pi, Pi (rysunek). Wektor normalny fi płaszczyzny rr jest kierunko-wego iii prostej l\. Można przyjąć, że ił = Oi = (1,2,3). Współrzędne

punktu Pi należącego do prostej Zi wyznaczamy tak jak w I sposobie, zatem Pi — (1.2,—3). Równanie płaszczyzny ir przechodzącej przez punkt Pi i prostopadłej do obu prostych ma postać

- : (x- 1,7,-2, = + 3)o (1,2,3) = O,

stąd

z: x + 2y -f- 3z + 4 == O.

Współrzędne punktu Pi są rozwiązaniami układu równań

f £ V _ £

ft : < 2 4 8’

\ x + 2» + 3z + 4 = 0.

/ 2 4 6\

Po rozwiązaniu tego układu otrzymamy ft = (—- Odległość d prostych równoległych li i li jest zatem równa

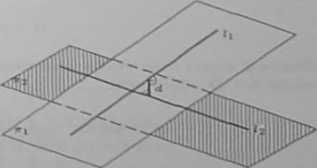
e) W rozwiązaniu wykorzystamy fakt mówiący, że odległość dwóch prostych skośnych jest równa odległości dwóch płaszczyzn równoległych zawierających te proste. Najpierw znajdziemy wektory kierunkowe 3i i tła odpowiednio prostych ii i I?. Wektor kierunkowy prostej li

jest równy 0|

= (0,1,0), a równy tła =

In

f x + p = l.

I * = Q.

prostej (a

(1,1.0). |

Wspólny wektor normalny fi płaszczyzn równoległych irt i »j zawierających odpowiednio proste i i i ta. jest prostopadły do obu wektorów. Można zatem przyjąć, że

rt = «, x 0_a = (0,1,0) x (1,1,0) = (0,0,-l).