DSC07367

152

Geometria analityczna w przestrzeni

_{?i = (0} , _3j    _ (7,-3,2), ft = (1.4.2) oraz mi = 3, m₃ = 1, mj = 2. Zatem

miń + mzft + »m?i.

^? " mi + mj + mj

= I[3(0.1.-3)+l(7.-3.2) + 2(l,4,2)|= (f.f.-j).

6

Środek masy tego układu jest w punkcie

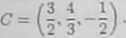
b)    Moment ł*zwładneści podanego układu mas względem osi O* wyraża się wzorem

/, = mi (y? + e?) + "»a (pi + z?) + mi (pi + i!) ,

gd**, p_{t =} (n,yi,zł) dla 1 $ i $ 3. Zatem dla podanego układu mas mamy U = 3(1 + 9) + 1(9 + 4) + 2(16 + 4) = 83.

c)    Mannit bezwładności układu mas względem prostej l wyraża sie wzorem

/i = midj +nu4 + mjdj,

d, jest odległością punktu P, od prostej i dla 1 $ i ^ 3. Niech P(t) — (3£, 3ł, £), gdzie t € R. będzie bieżącym punktem prostej 1. Wielkości d], d\, d\ wyznaczymy minimalizują: kwadrat długości odcinka łamiącego punkty P(t) i Pt dla 1 $ t $ 3. Mamy zatem

/(t) = |PiP(f)|^a = (3ł)^a + (3t - l)^a + (t + 3)^a = 19t^a +10,

s(£) = |ftP(t)l^a = (3t - 7)^a + (3t + 3)^a + (t - 3)^a = 19t^a - 28£ + 62,

fc(£) = |ftP(t)|^a = (3t - l)^a + (3t - 4)^a + (t- 2)^a = 19t* - 34t + 21.

Zauważmy, że funkcje /, g,h aą trójmianami kwadratowymi postaci ot^a + bt + c, gdzie

a > 0. Zatem waitcści najmniejsze przyjmują w punkcie t . = Stąd

2a

4-a--»©.^

Tak. Więc

/. = 34+4+24 = -^.

d) Siła przyciągania grawitacyjnego maay M = 4 o wektorze wodzącym r₀ = (0 0 0) przez układ punktów materialnych wyraża sie wzorem

f = CM

( fi-fo

Vlń-?o|³

mi +

fi-fo

r?CTT^{ma +}

\n-*o\

ft-fo In - roi³

gdzie C jest stałą grawitacji. Mamy więc

Zadania

153

Zadania

•    Zadanie 5.1

Obliczyć długości podanych wektorów:

a) 3 = (3, -1,12); b)b= (v/3,-\/5,2V2);

c)    c = [gcosip, psinip, /i), gdzie g > 0 oraz <p, h ę R;

d) 2 = (p cos p cos p sin <p cos    0 sin V>), gdzie p > 0 oraz g R.

•    Zadanie 5.2

Wektory o, b tworzą dwa sąsiednie boki trójkąta. Wyrazić środkowe tego trójkąta przez wektory a, b.

•    Zadanie 5.3

Znaleźć wersor u, który:

a)    leży w płaszczyźnie xOy i tworzy kąt o z dodatnią częścią osi Ox\

b)    tworzy z dodatnimi częściami osi Ox, Oy, Oz odpowiednio kąty ó, /?, 7;

c)    tworzy jednakowe kąty z wektorami 2 = (0,3, -4), b = (8,6,0) i jest położony w płaszczyźnie wyznaczonej przez te wektory.

•    Zadanie 5.4

Obliczyć iloczyny skalarne podanych par wektorów:

a)    2 = (1,-2,5), 5= (3.-1,0);

b)    -5 = 37— 2k, V = -i + 3j + 7k;

c)    1 = p + 2q — r, j/ = 3p — q + 2r, gdzie p, g, r są wersorami parami prostopadłymi.

•    Zadanie 5.5

Korzystając z iloczynu skalarnego obliczyć miary kątów między:

a)    wektorami o = (—3,0,4), b = (0,1, —2);

b)    wusiecznymi kątów utworzonych przez osie Ox, Oy oraz osie Oy, Oz układu Oxyz\

c)    przekątnymi równoleglościanu rozpiętego na wektorach u = (1,2,3), 3 = (-1,0, 2), 5 = (3,1, 5).

•    Zadanie 5.6

Obliczyć długość rzutu prostokątnego wektora 3 = (/2, i/3, -vS) na wektor

6 = (-%/§, 0, y/S).

•    Zadanie 5.7

Obliczyć iloczyny wektorowe podanych par wektorów:

a) 3 = (-3,2,0), £=(1,5,-2); b) u =2i- 3fc, v= t + j-Ak;

c) x = 2p + i} + f, $ = P + 35 + 43, gdzie j}, q, r są parami prostopadłymi wersorami o orientacji zgodnej z orientacją układu współrzędnych.