DSC07366

150

Geometria analityczna w przestrzeni

a równanie odcinka anteny przechodzącej przez punkty D i B postać

( x = 30a,

D B : < y = 40s,

l z = 25 — Ss,

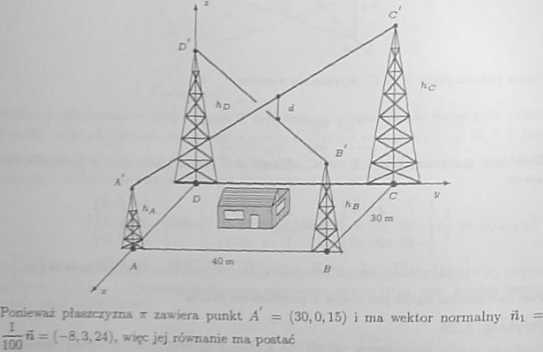
gdzie s € [0. lj. Szukana najmniejsza odległość d między tymi antenami jest odległością między odcinkami AC i D B . Odległość ta jest równa odległości dowolnego punktu odcinka D B (np. punktu D) od płaszczyzny ir zawierającej odcinek A C i równoległej do odcinka D B . Znajdziemy teraz równanie płaszczyzny >r. Wektor normalny fi tej

płaszczyzny ma postać

fi =AC x DB = (-30,40,15) x (30,40,-5) = 100(-8,3,24).

-8(z — 30) + 3{p — 0) +24(z — 16) = 0,

stąd

x: -8z + 3i/ + 24z- 120 = 0.

Skorzystamy teraz ze wzoru na odległość d punktu Pq = (zo.Po.zo) od płaszczyzny *: Ax + By+Cz+ D = 0-,

j _ IAxp + Byg + Czo + Oj

“ >/Aⁱ + IP + Ć'¹

Odległość punktu D = (0,0,25) od płaszczyzny r : -8z+3y+24i- 120 = 0 jest zatem równa

.    i-8• 0 + 3-0 + 24■ 26 —120|    480    ,

d =    - ■ r=    : : =- = === « 18,84 [ml.

_vć(-8)^a + 3³+24³    v849    ¹

Dla pełności rozważań niezbędne jest jeszcze sprawdzenie, czy najmniejsza odległość miedzy prostymi przechodzącymi przez punkty A , Cf oraz D , Ci jest roifeowatia przez

Przykłady

punkty odcinków AC i ti Ć. Sprawdzenie, że lak jest w tym przypadku, pozostawiamy Czytelnikowi.

Zastosowania rachunku wektorowego w mechanice*

• Przykład 5.30

Obliczyć sumę momentów sil F\ = (—1,2,3) oraz Fi — (0,1,—5) względem punktu O — (2,3,-1), jeżeli siły te są przyłożone odpowiednio w punktach P\ = (0,0,0,) oraz P₂ = (1,-3,4).

Rozwiązanie

Moment M siły F przyłożonej w punkcie P, rozważany względem punktu O, wyraża się

wzorem M =OP x F. Niech l&j i JWj oznaczają odpowiednio momenty sil Fi i Pi. Wtedy

= OPx X Fi = (—2? — 3y + fc) x (-i + 2j+3fc)

= —3fc —j —4lE —2* + 6y —9?= —lli + ój—7fc.

oraz

Mi = OP₂ xfj = (—? -6j + bit) x (J- 5fc)

= —fc — 5t — ój-t- 30? = 25? — 5] — k.

Moment wypadkowy tych sil jest zatem równy

Aj = M, + Sfi = (-11? + 5j- ~k) + (25?- 5j- k) = 14?- 8k.

• Przykład 5.31

W punktach P, = (0,1, -3), P_a = (7, -3,2), P₃ = (1,4,2) umieszczone są odpowiednio masy = 3, m₂ = 1, m₃ = 2. ^a) Wyznaczyć położenie środka masy tego układu;

h) Obliczyć moment bezwładności podanego układu mas względem osi Oz;

c)    Obliczyć moment bezwładności podanego układu mas względem prostej

l: x — y = 3z;

d)    Obliczyć silę przyciągania grawitacyjnego masy M — 4 znajdującej się w początku układu współrzędnych przez podany układ mas.

Rozwiązanie

a) Wektor wodzący r środka masy układu punktów materialnych o wektorach wodzących P, i masach im, gdzie 1 < * $ wyraża sie wzorem

_ miPi + mi IS + — + m„ mi -ł* ma + ... + m„

W układzie punktów materialnych rozważanym w zadaniu mamy: