DSC07350

118

Geometria analityczna w przestrzeni

jest równoległa do wektora

Rzut prostokątny dowolnego wektora na tę prostą jest taki sam jak rzut tego wektora na wektor 6. Rzut prostokątny 5 wektora a na wektor b (rysunek) wyraża się wzorem

1^.6

|6|^a

u =

Wzór ten wynika bezpośrednio z definicji iloczynu skalarnego wektorów a i 5. Rzut ii wektora 5 = (3.4. — 1) na wektor 6 = (1,1.1) ma zatem postać

u

(3.4,-l)o (1,1,1)

(>/!*+ 1*+T*)³

(1,1,1) = (2,2,2).

Stąd |u| = 2v^/3-

lloczyn wektorowy

• Przykład 5.7

Obliczyć iloczyny wektorowe podanych par wektorów:

a) 5 = (-1,3,2), 6 = (-1,2,-5); b) p = 2j+ k, q=i-j+3k.

Rozwiązanie

a) Do obliczenia iloczynu wektorowego wektorów 5 = (zi.yi.zi) i 6 = (x3.y3.-2) wykorzystamy wzór

i	i
*t	Vl
*3	V3	-2

a x

7atem

i 3 k

-13 2 -1 2 -5

3x6 = (-1,3.2) x (-1,2,-6) =

= *[3- (-5) - 2 - 2] - J[(-l) - (-5) - (-1) - 2] + k[(-1) - 2 - (-O ' ³1 = -IBi - 7]+ i = (-10, -7.1).

b) W rozwiązaniu wykorzystamy własności iloczynu wektorowego oraz równości J x j = i, j x i <= t. k x i = j, ix i = Jx J= ix 1= 8.

Mamy

= (2j+i) x (ś-J+3fc)

= 2(Jx ij-2(Jxj)+6(jxfc) ₊ (fcxJ)-(/;x J)+3(Z*k) = -2* -d+bi+}+i+d=x7i+j-2k.

Uwaga. Przykład b) można oczywiście obliczyć sposobem przedstawionym w a) po zapisaniu p = (0,2,1), 3 = (1, —1,3).

• Przykład 5.8

Obliczyć pola podanych powierzchni:

a)    trójkąt rozpięty na wektorach o=* (1,—1,1), b = (0,3,-2);

b)    równoleglobok o trzech kolejnych wierzchołkach w punktach A = (1,0,1), B = (3,-l,5),Ć = (-1,5,0);

c)    równoległościan rozpięty na wektorach p, q, r.

Rozwiązanie

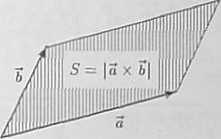
W rozwiązaniu wykorzystamy określenie iloczynu wektorowego, z którego m. in. wynika, że pole S równoległoboku rozpiętego na wektorach 5, b jest równe długości wektora a x b:

S = |a x b|.

a) Ponieważ pole trójkąta rozpiętego na wektorach a, b jest równe połowie pola równo-ległoboku rozpiętego na tych wektorach, więc

S=i|axb|=i|(l,-l,l)x(0,3,-2)|

i 3 k 1 -1 1 0 3-2

= ól-* + 2j + 3*| =

b) Równoleglobok ABCD o wierzchołkach w punktach A = (1,0,1), B = (3,—1,5), C = (—1,5,0) jest rozpięty na wektorach

AB= (2,-1,4), AC= (-2,5,-1),

zatem jego pole wyraża się wzorem

7 i a

2-1 4 | -2    5-1

Sadcd — | AB x AC

= |-19t-6y + 8ib| = ^(-19)* + (—6)^a + 8? = V46T a 21,47.

c) Powierzchnia równoległościanu rozpiętego na wektorach p, i}, P składa się z dwóch równolegloboków rozpiętych na wektorach p, tj, z dwócłi równoległoboków rozpiętych na wektoracli p, ? oraz dwócłi równolegloboków rozpiętych na wektorach i], P. Pole tej powierzchni będzie zatem równe

5 = 2(|p x ę| + |0 x r| + |3x ?|).