DSC07365

148

Geometria analityczna

w przestrzeni

Rozwiązanie

Sytuacją opisaną w zadaniu przedstawiono na rysunku poniżej. Układ współrzędnych dobrano w ten sposób, aby rurociąg wychodził z ziemi w punkcie przebicia stoku z osią Oz . a oś Oy leżała pod rurociągiem.

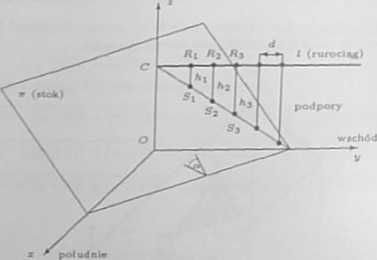
Ponieważ płaszczyzna x (stok) opada w kierunku południowo-wschodnim pod kątem a = 30°, więc jej równanie ma postaó ir : -Ę= + -4= + z = c, gdzie C = (0,0, c) jest

t/6    y/6

punktem przebicia rurociągu z osią Oz. Ponadto, skoro prosta / (rurociąg) przebiega poziomo z zachodu na wichód, więc jej równanie ma postaó

f * = °.

‘ = < V = t. gdzie t £ R.

I * = c,

W > sokości podpór będą równe odległościom punktów ft, rurociągu od punktów Sn stoku, gdzie n = 1.2,3.....Ponieważ podpory są mocowane co d = 10 m, więc punkty moco

wania mają współrzędne

= (°.

A. = (0.10n,c). S,

10n,c

10n\

J.y'?-/'

gdzie n = 1,2,3.....Stąd A„ =    E^zie n = 1,2,3.....Przyjmując

rt = 1,2,3 otrzymamy Aj as 4,08 m. Aa = 8,16 m, Aa s= 12,25 m.

• Przykład 5.28

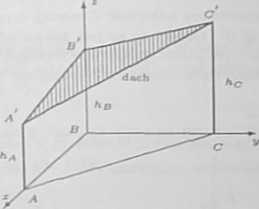
Hala widowiskowa ma kształt trójkąta prostokątnego ABC o przyprostokątnych AB = 90 m, BC = 120 m. Płaski dach nad tą halą oparty jest na trzech pionowych podporach zamocowanych w punktach A, B, C. Wysokości tych podpór są równe odpowiednio h_A = 15 m, Ap = 20 m, h_c = 25 m. Obliczyć pole powierzchni tego dsrłm.

Rozwiązanie

Sytuację omawianą w zadaniu przedstawiono na rysunkuniiej. Współrzędne wierzchołków A . B , ćf dachu są wtedy równe A' = (00,0,15), B = (0,0,20), C = (0,120,25).

przykłady

Do obliczenia polo powierzchni dachu wykorzystamy iloczyn wektorowy. Pole trójkąta rozpiętego no wektoroch o, 6 wyraża się wzorem

5 = i|3x 6|.

Zatem pole trójkąta ABC wyraża się wzorem

B'c' ⁼    X. AC |.

Obliczymy teraz wektory A'B', XĆ. Mamy A'b'= (-90,0.5), AC = (-90,120,10). Zatem

* 3 k		* 3 *		Z 3 k
-90 0 5	1 — 251	-18 0 1	l=25|	-18 0 l
-90 120 10		-9 12 1		-27 12 0

= 251 — 12» + 9j — 2l6fc| = 25_v/12³ +9² + 216³ = 75%/5209 « 5413 [m³] .

^St±A'B'c'

Pole powierzchni dachu jest równe w przybliżeniu 5413m³.

• Przykład 5.29

Radiowa stacja nasłuchowa składa się z dwóch prostoliniowych anten zawieszonych na dwóch parach pionowych slupów. W każdej parze slupy ustawione są w przeciwległych wierzchołkach prostokąta ABCD o bokach AB = 40 m i AD = 30 in. Wysokości slupów ustawionych w punktach A, B,C, D są równe odpowiednio = 15 m, hg = 20 m, hc = 30 m, ho = 25 m. Obliczyć najmniejszą odległość między antenami.

Rozwiązanie

Sytuację opisaną w zadaniu przedstawiono na rysunku niżej. Osie Ox i Oy układu współrzędnych pokrywają się z bokami prostokąta, a oś Oz pokrywa się z jednym ze słupów. W tym układzie współrzędnych wierzchołki slupów, tj. punkty A , B', C', O'. mają współrzędne (podano w metrach) A = (30,0,15), B' = (30,40,20), C' = (0,40,30), D' = (0,0,25). Równanie odcinka anteny przechodzącej przez punkty X, C' ma postać ; , r x = 30 — 30t,

AC : < y = 4 Ot,    gdzie t € 10, II,

l = = 15 + 161.