matma5

A\. h Tłl

1)    Sprawdź czy funkcja <?(*) = 4z_t + 6x, - 2z,x_a - 2x\ - 2x\ ma punkt stacjonarny w punkcie x = (0,1).

a. tak,

0 nic.

2)    Wykorzystując algorytm najszybszego spadku numerycznego poszukiwania ekstremum funkcji, należy zdecydować, w którym kierunku należy zrealizować krok d (przemieszczenie) startując z punktu z° = (l,0), aby zbliżyć się do punktu maksymalnego funkcji: Q(x) = 2x, + 3x, - x,.v, - ** - x*.

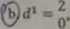
a.    2--I,

b.    A - -0,5

c.    A-O, ® A ^m 0,5, e. *-l.

3) Dla problemu zdefiniowanego w poprzednim pytaniu i wyznaczonego kierunku poszukiwań d' należy zdecydować, jaką długość kroku (przemieszczenia) \ powinno się wykonać wzdłuż kierunku d' startując z punktu z®-(1,0), aby zbliżyć się do punktu minimalnego funkcji: Q(x) = 2x, + 3x₂ - x,x, - *? -

*1) Dla problemu optymalizacyjnego określonego w pytaniu 2 wylosowano nowy

wybieranych losowo. Startując z punktu z⁰ “ (1,0), dla przyjętej długości kroku A “ 1, wartość funkcji celu Q(x) w nowym punkcie z¹ będzie wynosiła:

a.    &x') - -2,75,

b.    £?(x^,)*-1.75.

0 żadna z. powyższych możliwości nie jest poprawna,

d. na podstawie danych określonych w zadaniu nic jest możliwe wyznaczenie wartości Q(x^l).

5) Funkcja Q(x) = — x + x³ ma maksimum na przedziale <-l,l>, które należy wyznaczyć. Na podstawie pochodnej funkcji Q’(x =0) należy zdecydować, jak zawęzić przeszukiwany przedział przeszukiwania. Kolejno przeszukiwanym przedziałem powinien być:

Ł <0,1>,

(b) <-1.0>.

c.    <-0,5;0>,

d.    <0; 0,5>,

c. żaden z powyższych.

6) Przedsiębiorstwo ma dwa pojazdy dysponujące różnymi możliwościami przewozowymi. Pojazd 1 może jednorazowo przewieźć na pewnej trasie 1000 kg towaru A oraz 3000 kg towaru B. oraz 5000 kg towaru C. Pojazd 2 może przewieźć jednorazowo 2000 kg towaru A oraz B. oraz C. Przedsiębiorstwo ma do przewozu 24000 kg towaru A. 32000 kg towaru B. 40000 kg towaru C. Jak przewieźć ładunek po minimalnych kosztach, wiedząc. Ze koszt jednego kursu na tej trasie wynosi dla pojazdu I 280 zl, dla pojazdu 2 - 200 zl. NaleZy zdecydować ile zmiennych powinno być w modelu matematycznym pozwalającym optymalizować problem (nie

należy liczyć warunku.« > 0):

samą wartość dl,

^,a różnic w

"Wodą róh

a. 2 zmienne, 3 zmienne.

7)    W odniesieniu do treści zadania z poprzedniego pytania (6), ile ograniczeń będzie posiadał model?

a.    1 ograniczenie,

b.    2 ograniczenia,

X 3 ograniczenia,

£d? 6 ograniczeń.

8)    Nowy typ paliwa ma być produkowany z dwóch istniejących surowców "A* i "B” Wymagania dla nowego paliwa:

-    powinno zawierać co najmniej 0.6% parafiny i 0,25% siarki.

-    temperatura topnienia nowego paliwa powinna być nie niższa niż -SOoC

Jednostka surowca "A" zawiera: 0.8% parafiny i 0,4% siarki, zaś jednostka surowca "B" zawiera 0.2% parafiny i 0,4% siarki. Temperatura topnienia surowca "A" wynosi -20oC,    surowca    “B":

-60oC. Jak wyprodukować co najmniej 900 jednostek nowego paliwa, aby ponieść minimalne koszty produkcji, zakładając że jednostka surowca “A" kosztuje 2$ zaś jednostka surowca "B" - 4$?

W związku z powyższym zadaniem należy zdecydować ile ograniczeń będzie miał model matematyczny zagadnienia (nie należy liczyć warunku j > OJ: fi) 4 ograniczenia.

b.    5 ograniczeń,

c.    6 ograniczeń

9)    Jaka będzie wartość i wymiar (jednostka) funkcji celu w problemie nr 8? Proszę napisać WARTOŚĆ funkcji celu w rozwiązaniu optymalnym (aby ją uzyskać, konieczne jest rozwiązanie zadania) i jednostkę, w jakiej wyrażona będzie funkcja celu.

10) Czy rozwiązanie optymalne ulegnie zmianie, jeśli ograniczenie dotyczące ilości nowego paliwa zostanie zniesione?

tak,

nic.

b