82830 img313 (6)

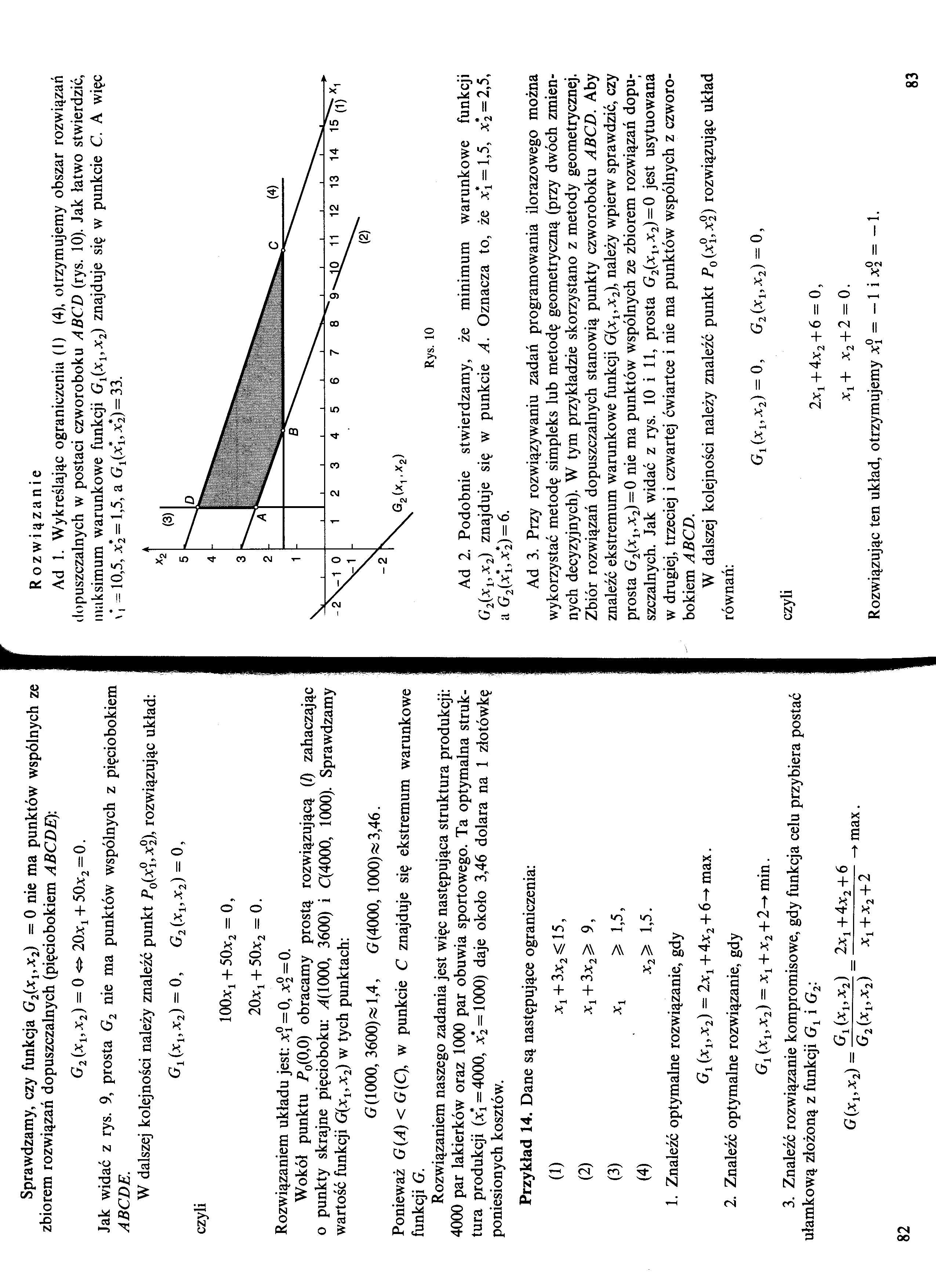
Sprawdzamy, czy funkcja G₂(x₁,x₂) = O nie ma punktów wspólnych ze zbiorem rozwiązań dopuszczalnych (pięciobokiem ABCDE):

G₂{x_ux₂) = 0 o 20x₁ + 50x₂ = 0.

Jak widać z rys. 9, prosta G₂ nie ma punktów wspólnych z pięciobokiem ABCDE.

W dalszej kolejności należy znaleźć punkt P_Q(x⁰ux⁰2), rozwiązując układ: (?j (xj, x₂) = 0, G₂ {x₂, x₂) = 0,

czyli

100*! + 50x₂ = 0,

20^! + 50*2 = 0.

Rozwiązaniem układu jest: x°_l = 0, x₂ = 0.

Wokół punktu ,P_o(0,0) obracamy prostą rozwiązującą (l) zahaczając o punkty skrajne pięcioboku: ,4(1000, 3600) i C(4000, 1000). Sprawdzamy wartość funkcji G(x_u x₂) w tych punktach:

G (1000, 3600) * 1,4,    G (4000, 1000)« 3,46.

Ponieważ G(A) < G(Q, w punkcie C znajduje się ekstremum warunkowe funkcji G.

Rozwiązaniem naszego zadania jest więc następująca struktura produkcji: 4000 par lakierków oraz 1000 par obuwia sportowego. Ta optymalna struktura produkcji (xi=4000, X2 = 1000) daje około 3,46 dolara na 1 złotówkę poniesionych kosztów.

Przykład 14. Dane są następujące ograniczenia:

(1)    X₁ + 3x₂<15,

(2)    + 3x₂ ^ 9,

(3)    x_t ^ 1,5,

(4)    x₂^ 1,5.

1.    Znaleźć optymalne rozwiązanie, gdy

G₁(x₁,x₂) = 2x_t + 4x₂ + 6-> max.

2.    Znaleźć optymalne rozwiązanie, gdy

G₁(x₁,x₂) = x₁-t-x₂-t-2->min.

3. Znaleźć rozwiązanie kompromisowe, gdy funkcja celu przybiera postać ułamkową złożoną z funkcji G_x i G₂:

G(x i,x₂) =

Gi (xi,x₂) _ 2xj +4x₂ + 6 G₂{x _l5x₂)    x₁ + x₂ + 2

max.

Rozwiązanie

Ad 1. Wykreślając ograniczenia (I) (4), otrzymujemy obszar rozwiązań dopuszczalnych w postaci czworoboku ABCD (rys. 10). Jak łatwo stwierdzić, maksimum warunkowe funkcji G_l(x_i,x₂) znajduje się w punkcie C. A więc

\j =10,5, x\ = 1,5, a G₁(**₁,*2) = 33.

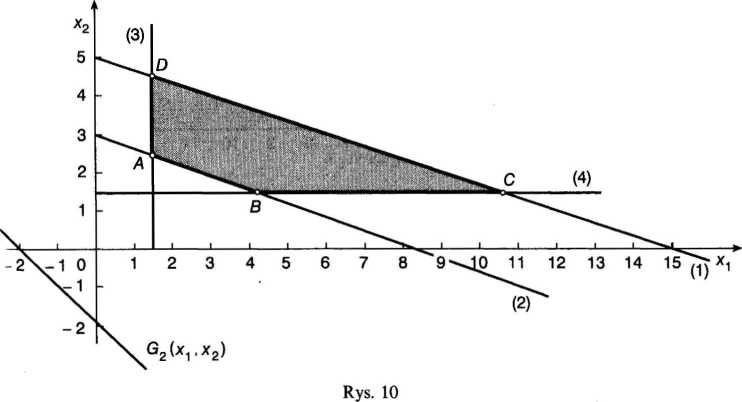
Ad 2. Podobnie stwierdzamy, że minimum warunkowe funkcji G₂{x_l,x₂) znajduje się w punkcie A. Oznacza to, że *j = 1,5, *2 = 2,5, a G₂(**i,*2) = 6.

Ad 3. Przy rozwiązywaniu zadań programowania ilorazowego można wykorzystać metodę simpleks lub metodę geometryczną (przy dwóch zmiennych decyzyjnych). W tym przykładzie skorzystano z metody geometrycznej. Zbiór rozwiązań dopuszczalnych stanowią punkty czworoboku ABCD. Aby znaleźć ekstremum warunkowe funkcji G(x₁,x₂), należy wpierw sprawdzić, czy prosta G₂(*₁,*₂)=0 nie ma punktów wspólnych ze zbiorem rozwiązań dopuszczalnych. Jak widać z rys. 10 i 11, prosta G₂(x_ux₂) = 0 jest usytuowana w drugiej, trzeciej i czwartej ćwiartce i nie ma punktów wspólnych z czworobokiem ABCD.

W dalszej kolejności należy znaleźć punkt P₀(^xi>^x2) rozwiązując układ równań:

G₁(*₁,*₂) = 0.    G₂(x₁,x₂) = 0,

czyli

2*j + 4*2 + 6 = 0,

*j +    *2 + 2 = 0.

Rozwiązując ten układ, otrzymujemy x° — — 1 i *° = — 1.

83